Quadrotor Trajectory Tracking with Learned Dynamics: Joint Koopman-based Learning of System Models and Function Dictionaries

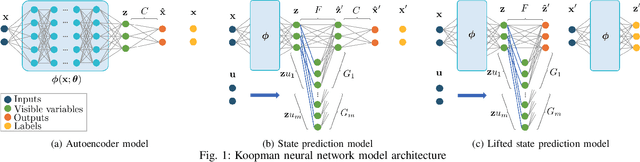
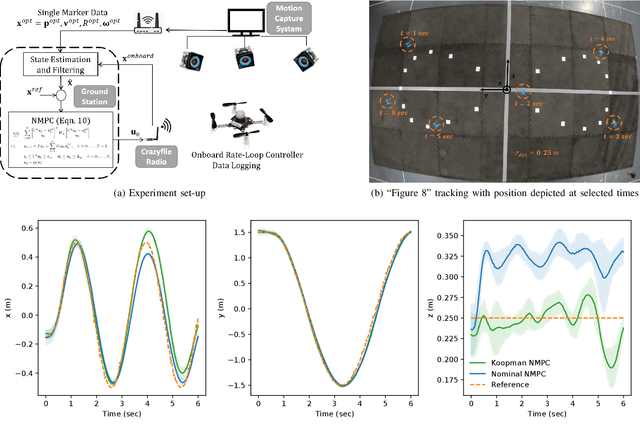
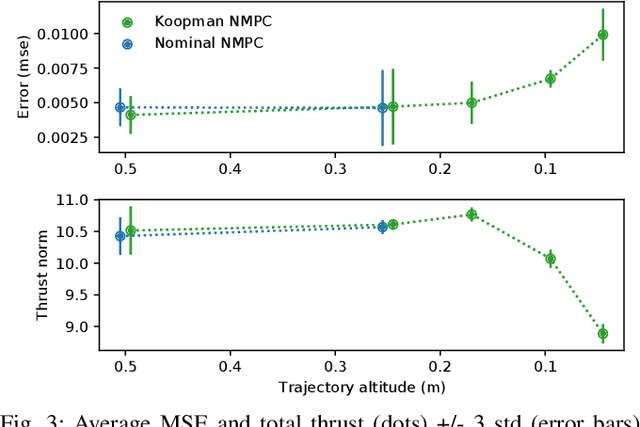
Nonlinear dynamical effects are crucial to the operation of many agile robotic systems. Koopman-based model learning methods can capture these nonlinear dynamical system effects in higher dimensional lifted bilinear models that are amenable to optimal control. However, standard methods that lift the system state using a fixed function dictionary before model learning result in high dimensional models that are intractable for real time control. This paper presents a novel method that jointly learns a function dictionary and lifted bilinear model purely from data by incorporating the Koopman model in a neural network architecture. Nonlinear MPC design utilizing the learned model can be performed readily. We experimentally realized this method on a multirotor drone for agile trajectory tracking at low altitudes where the aerodynamic ground effect influences the system's behavior. Experimental results demonstrate that the learning-based controller achieves similar performance as a nonlinear MPC based on a nominal dynamics model in medium altitude. However, our learning-based system can reliably track trajectories in near-ground flight regimes while the nominal controller crashes due to unmodeled dynamical effects that are captured by our method.

Koopman NMPC: Koopman-based Learning and Nonlinear Model Predictive Control of Control-affine Systems

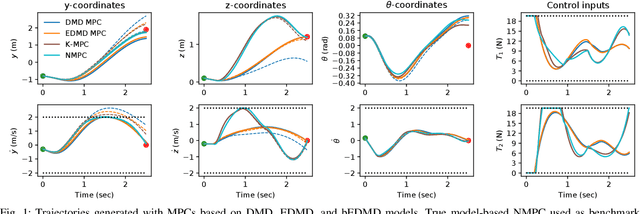
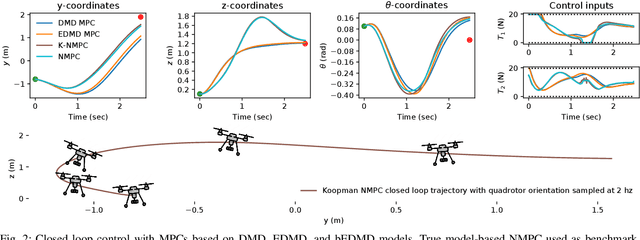
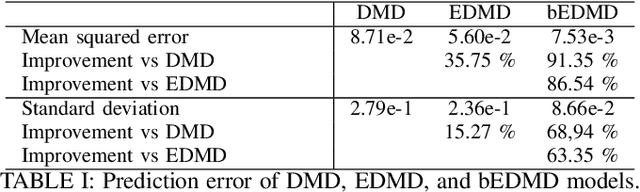
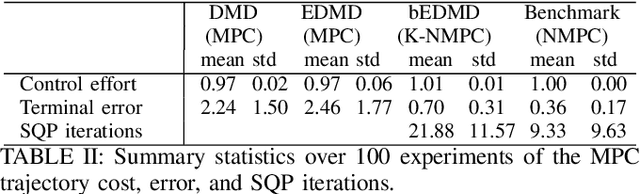
Koopman-based learning methods can potentially be practical and powerful tools for dynamical robotic systems. However, common methods to construct Koopman representations seek to learn lifted linear models that cannot capture nonlinear actuation effects inherent in many robotic systems. This paper presents a learning and control methodology that is a first step towards overcoming this limitation. Using the Koopman canonical transform, control-affine dynamics can be expressed by a lifted bilinear model. The learned model is used for nonlinear model predictive control (NMPC) design where the bilinear structure can be exploited to improve computational efficiency. The benefits for control-affine dynamics compared to existing Koopman-based methods are highlighted through an example of a simulated planar quadrotor. Prediction error is greatly reduced and closed loop performance similar to NMPC with full model knowledge is achieved.