Variational Inference: Posterior Threshold Improves Network Clustering Accuracy in Sparse Regimes

Variational inference has been widely used in machine learning literature to fit various Bayesian models. In network analysis, this method has been successfully applied to solve the community detection problems. Although these results are promising, their theoretical support is only for relatively dense networks, an assumption that may not hold for real networks. In addition, it has been shown recently that the variational loss surface has many saddle points, which may severely affect its performance, especially when applied to sparse networks. This paper proposes a simple way to improve the variational inference method by hard thresholding the posterior of the community assignment after each iteration. Using a random initialization that correlates with the true community assignment, we show that the proposed method converges and can accurately recover the true community labels, even when the average node degree of the network is bounded. Extensive numerical study further confirms the advantage of the proposed method over the classical variational inference and another state-of-the-art algorithm.

Network Estimation by Mixing: Adaptivity and More

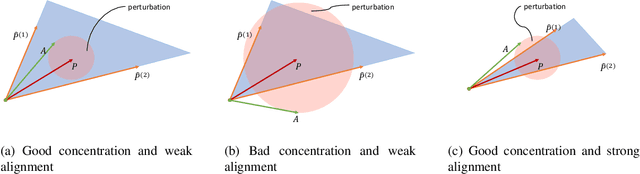
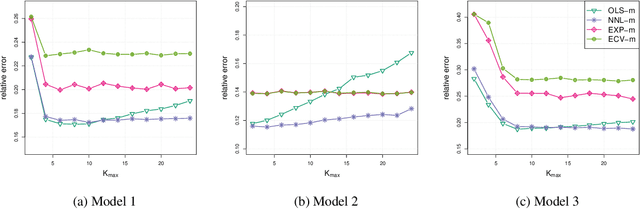
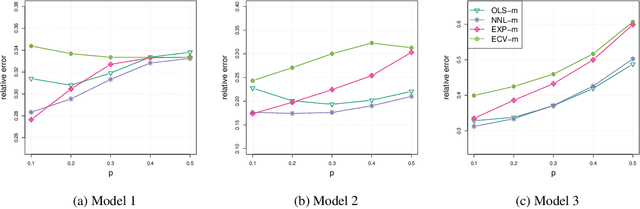
Networks analysis has been commonly used to study the interactions between units of complex systems. One problem of particular interest is learning the network's underlying connection pattern given a single and noisy instantiation. While many methods have been proposed to address this problem in recent years, they usually assume that the true model belongs to a known class, which is not verifiable in most real-world applications. Consequently, network modeling based on these methods either suffers from model misspecification or relies on additional model selection procedures that are not well understood in theory and can potentially be unstable in practice. To address this difficulty, we propose a mixing strategy that leverages available arbitrary models to improve their individual performances. The proposed method is computationally efficient and almost tuning-free; thus, it can be used as an off-the-shelf method for network modeling. We show that the proposed method performs equally well as the oracle estimate when the true model is included as individual candidates. More importantly, the method remains robust and outperforms all current estimates even when the models are misspecified. Extensive simulation examples are used to verify the advantage of the proposed mixing method. Evaluation of link prediction performance on 385 real-world networks from six domains also demonstrates the universal competitiveness of the mixing method across multiple domains.

Estimating the number of communities in networks by spectral methods

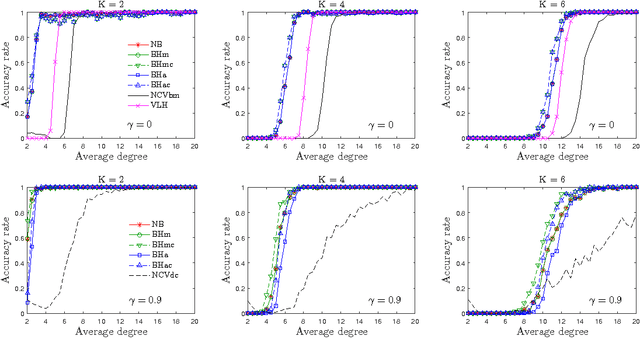
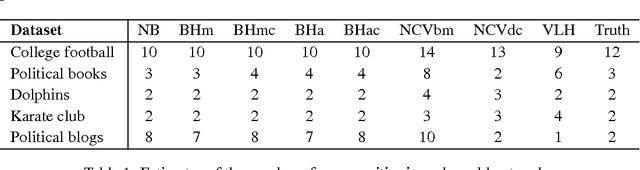
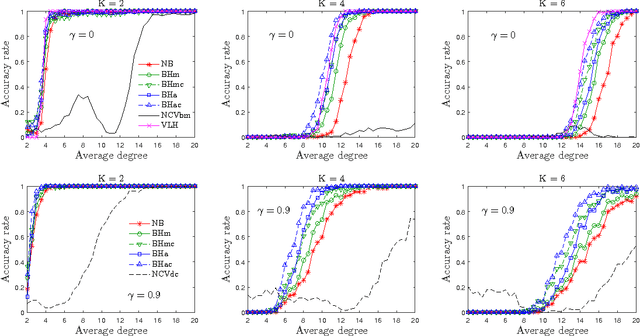
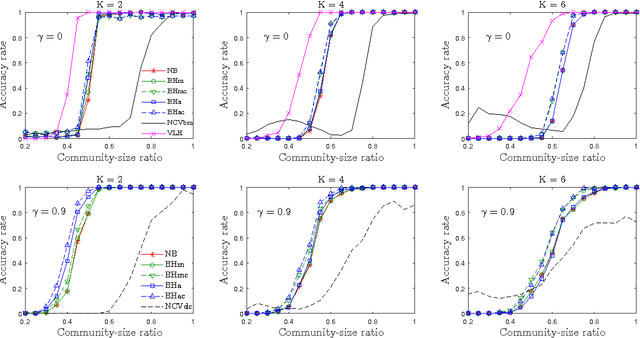
Community detection is a fundamental problem in network analysis with many methods available to estimate communities. Most of these methods assume that the number of communities is known, which is often not the case in practice. We propose a simple and very fast method for estimating the number of communities based on the spectral properties of certain graph operators, such as the non-backtracking matrix and the Bethe Hessian matrix. We show that the method performs well under several models and a wide range of parameters, and is guaranteed to be consistent under several asymptotic regimes. We compare the new method to several existing methods for estimating the number of communities and show that it is both more accurate and more computationally efficient.

Optimization via Low-rank Approximation for Community Detection in Networks

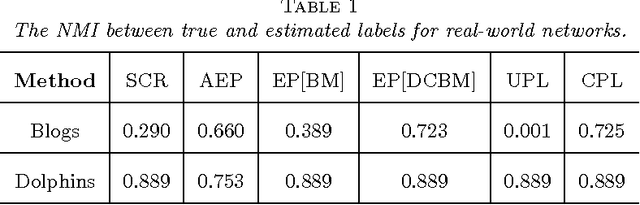
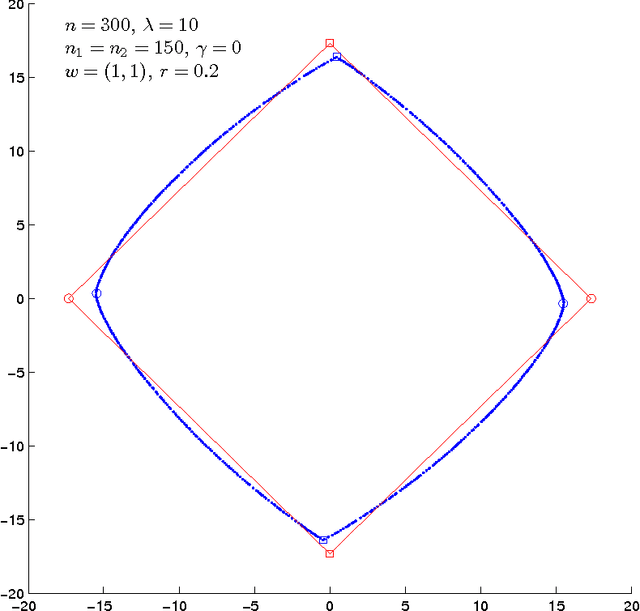
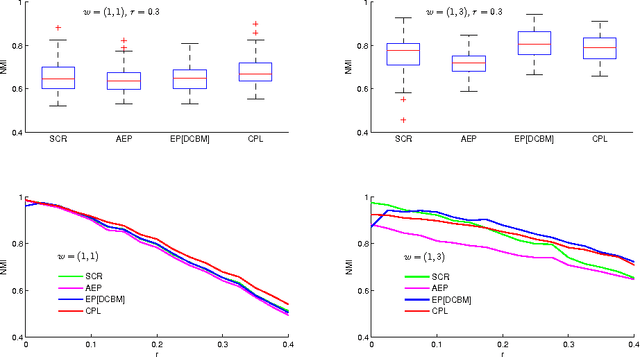
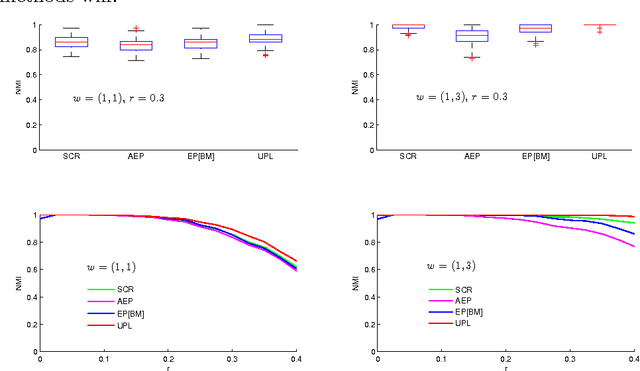
Community detection is one of the fundamental problems of network analysis, for which a number of methods have been proposed. Most model-based or criteria-based methods have to solve an optimization problem over a discrete set of labels to find communities, which is computationally infeasible. Some fast spectral algorithms have been proposed for specific methods or models, but only on a case-by-case basis. Here we propose a general approach for maximizing a function of a network adjacency matrix over discrete labels by projecting the set of labels onto a subspace approximating the leading eigenvectors of the expected adjacency matrix. This projection onto a low-dimensional space makes the feasible set of labels much smaller and the optimization problem much easier. We prove a general result about this method and show how to apply it to several previously proposed community detection criteria, establishing its consistency for label estimation in each case and demonstrating the fundamental connection between spectral properties of the network and various model-based approaches to community detection. Simulations and applications to real-world data are included to demonstrate our method performs well for multiple problems over a wide range of parameters.