LS-DYNA Machine Learning-based Multiscale Method for Nonlinear Modeling of Short Fiber-Reinforced Composites

Short-fiber-reinforced composites (SFRC) are high-performance engineering materials for lightweight structural applications in the automotive and electronics industries. Typically, SFRC structures are manufactured by injection molding, which induces heterogeneous microstructures, and the resulting nonlinear anisotropic behaviors are challenging to predict by conventional micromechanical analyses. In this work, we present a machine learning-based multiscale method by integrating injection molding-induced microstructures, material homogenization, and Deep Material Network (DMN) in the finite element simulation software LS-DYNA for structural analysis of SFRC. DMN is a physics-embedded machine learning model that learns the microscale material morphologies hidden in representative volume elements of composites through offline training. By coupling DMN with finite elements, we have developed a highly accurate and efficient data-driven approach, which predicts nonlinear behaviors of composite materials and structures at a computational speed orders-of-magnitude faster than the high-fidelity direct numerical simulation. To model industrial-scale SFRC products, transfer learning is utilized to generate a unified DMN database, which effectively captures the effects of injection molding-induced fiber orientations and volume fractions on the overall composite properties. Numerical examples are presented to demonstrate the promising performance of this LS-DYNA machine learning-based multiscale method for SFRC modeling.

Intelligent multiscale simulation based on process-guided composite database

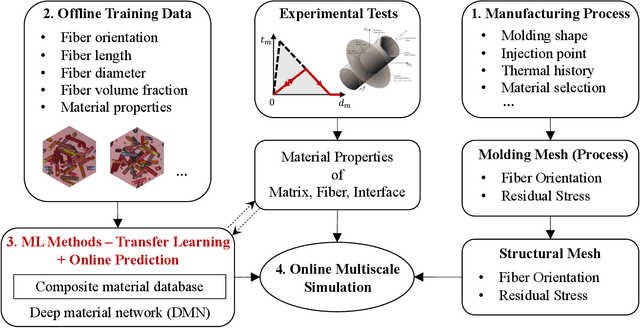
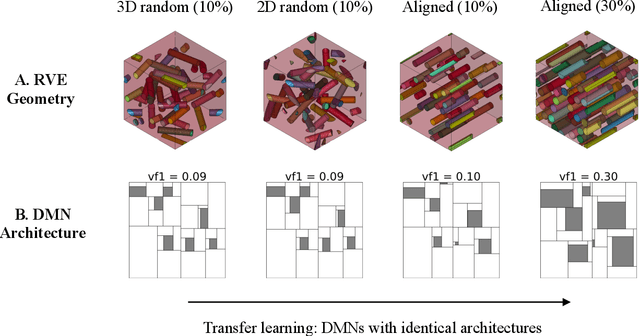
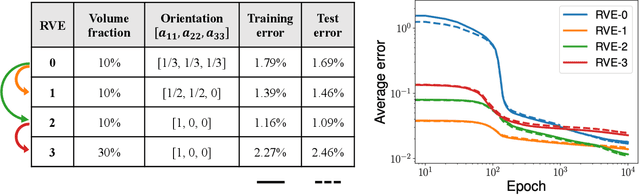
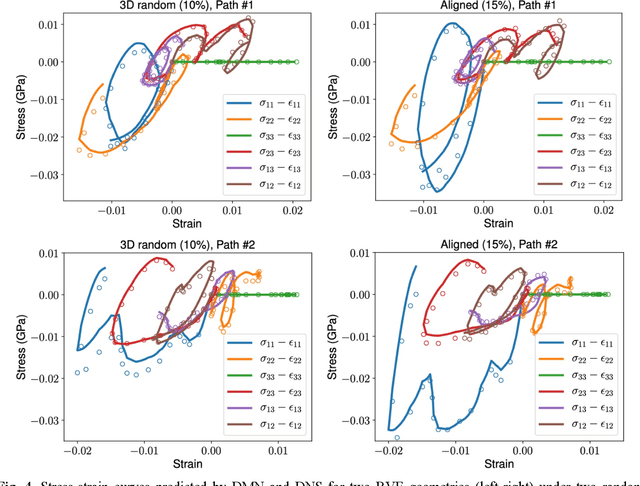
In the paper, we present an integrated data-driven modeling framework based on process modeling, material homogenization, mechanistic machine learning, and concurrent multiscale simulation. We are interested in the injection-molded short fiber reinforced composites, which have been identified as key material systems in automotive, aerospace, and electronics industries. The molding process induces spatially varying microstructures across various length scales, while the resulting strongly anisotropic and nonlinear material properties are still challenging to be captured by conventional modeling approaches. To prepare the linear elastic training data for our machine learning tasks, Representative Volume Elements (RVE) with different fiber orientations and volume fractions are generated through stochastic reconstruction. More importantly, we utilize the recently proposed Deep Material Network (DMN) to learn the hidden microscale morphologies from data. With essential physics embedded in its building blocks, this data-driven material model can be extrapolated to predict nonlinear material behaviors efficiently and accurately. Through the transfer learning of DMN, we create a unified process-guided material database that covers a full range of geometric descriptors for short fiber reinforced composites. Finally, this unified DMN database is implemented and coupled with macroscale finite element model to enable concurrent multiscale simulations. From our perspective, the proposed framework is also promising in many other emergent multiscale engineering systems, such as additive manufacturing and compressive molding.

Exploring the 3D architectures of deep material network in data-driven multiscale mechanics

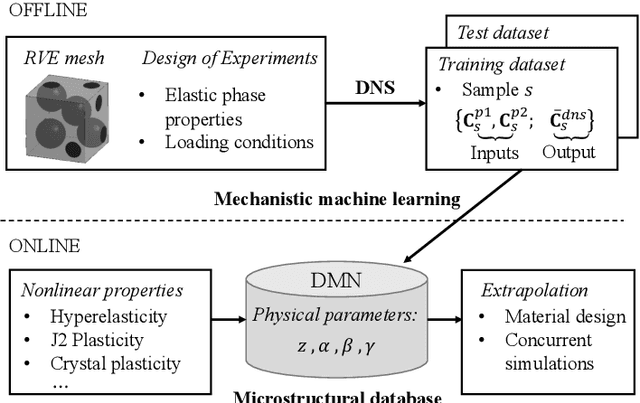
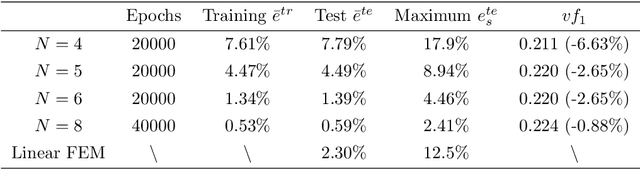
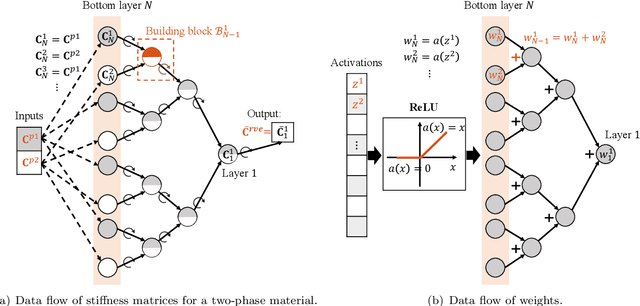
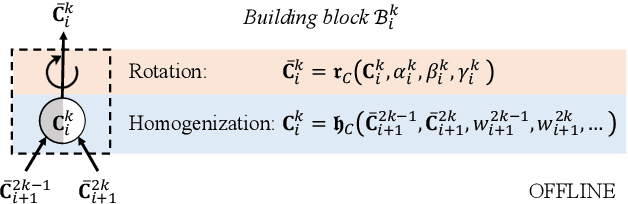
This paper extends the deep material network (DMN) proposed by Liu et al. (2018) to tackle general 3-dimensional (3D) problems with arbitrary material and geometric nonlinearities. The global framework of DMN for mechanistic data-driven multiscale material modeling is discussed in detail on the offline training and online extrapolation stages. Analytical solutions of the 3D building block with a two-layer structure in both small- and finite-strain formulations are derived based on interfacial equilibrium conditions and kinematic constraints. With linear elastic data generated by direct numerical simulations on a representative volume element (RVE), the network can be effectively trained in offline stage using stochastic gradient descent and advanced model compression algorithms. Efficiency and accuracy of DMN on addressing the long-standing 3D RVE challenges with complex morphologies and material laws are validated through numerical experiments, including 1) hyperelastic particle-reinforced rubber composite with Mullins effect; 2) polycrystalline materials with rate-dependent crystal plasticity; 3) carbon fiber reinforced polymer (CFRP) composites with fiber anisotropic elasticity and matrix plasticity. In particular, we demonstrate a three-scale homogenization procedure of CFRP system by concatenating the microscale and mesoscale material networks. The complete learning and extrapolation procedures of DMN establish a reliable data-driven framework for multiscale material modeling and design.