Answering Conjunctive Queries over $\mathcal{EL}$ Knowledge Bases with Transitive and Reflexive Roles

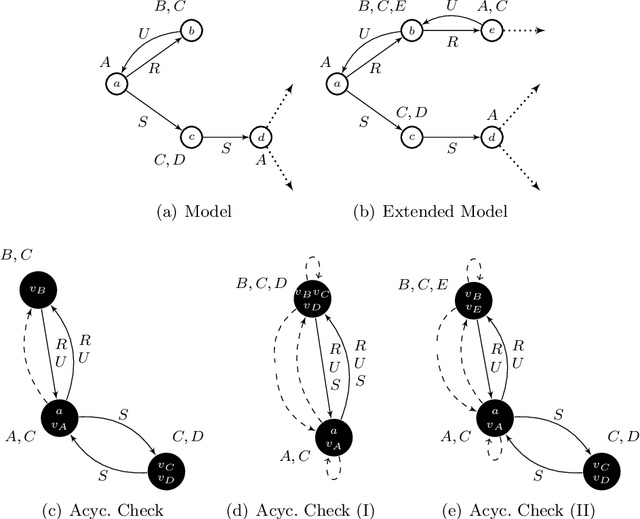
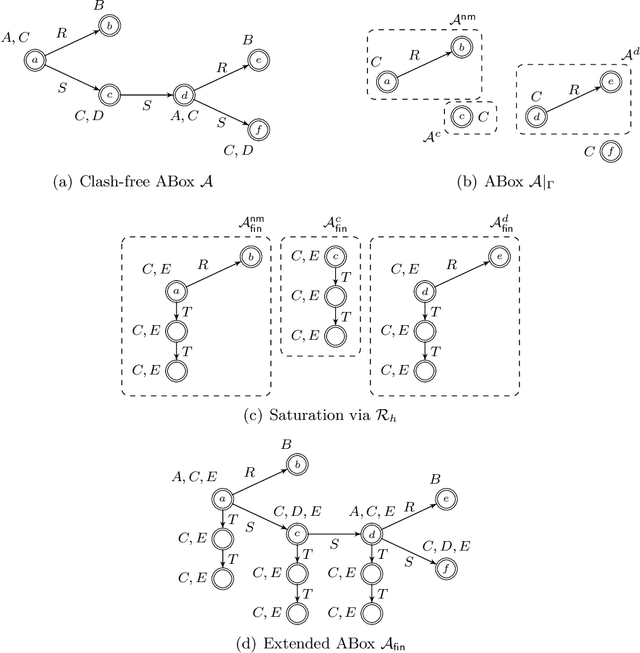
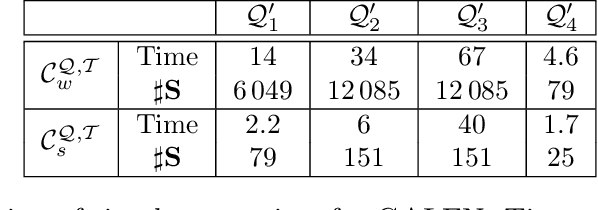
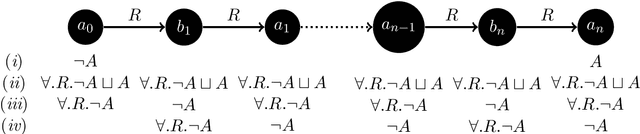
Answering conjunctive queries (CQs) over $\mathcal{EL}$ knowledge bases (KBs) with complex role inclusions is PSPACE-hard and in PSPACE in certain cases; however, if complex role inclusions are restricted to role transitivity, the tight upper complexity bound has so far been unknown. Furthermore, the existing algorithms cannot handle reflexive roles, and they are not practicable. Finally, the problem is tractable for acyclic CQs and $\mathcal{ELH}$, and NP-complete for unrestricted CQs and $\mathcal{ELHO}$ KBs. In this paper we complete the complexity landscape of CQ answering for several important cases. In particular, we present a practicable NP algorithm for answering CQs over $\mathcal{ELHO}^s$ KBs---a logic containing all of OWL 2 EL, but with complex role inclusions restricted to role transitivity. Our preliminary evaluation suggests that the algorithm can be suitable for practical use. Moreover, we show that, even for a restricted class of so-called arborescent acyclic queries, CQ answering over $\mathcal{EL}$ KBs becomes NP-hard in the presence of either transitive or reflexive roles. Finally, we show that answering arborescent CQs over $\mathcal{ELHO}$ KBs is tractable, whereas answering acyclic CQs is NP-hard.

Handling owl:sameAs via Rewriting

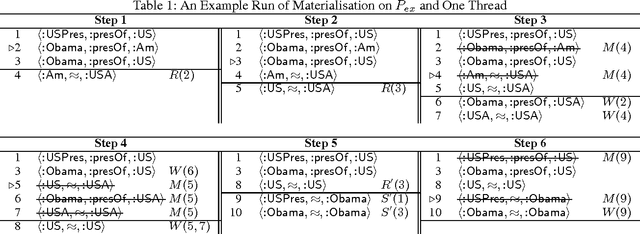
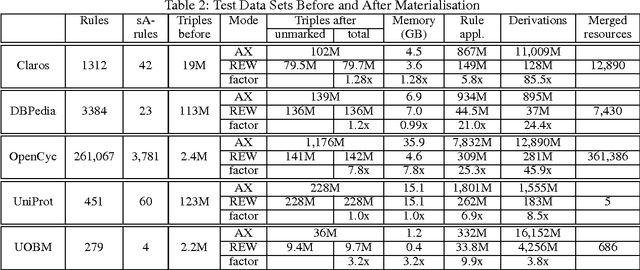
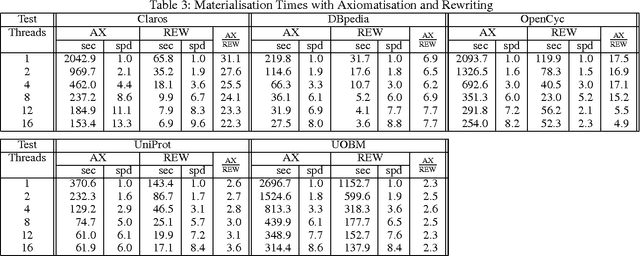
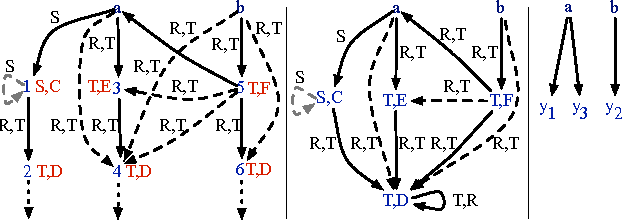
Rewriting is widely used to optimise owl:sameAs reasoning in materialisation based OWL 2 RL systems. We investigate issues related to both the correctness and efficiency of rewriting, and present an algorithm that guarantees correctness, improves efficiency, and can be effectively parallelised. Our evaluation shows that our approach can reduce reasoning times on practical data sets by orders of magnitude.

Acyclicity Notions for Existential Rules and Their Application to Query Answering in Ontologies

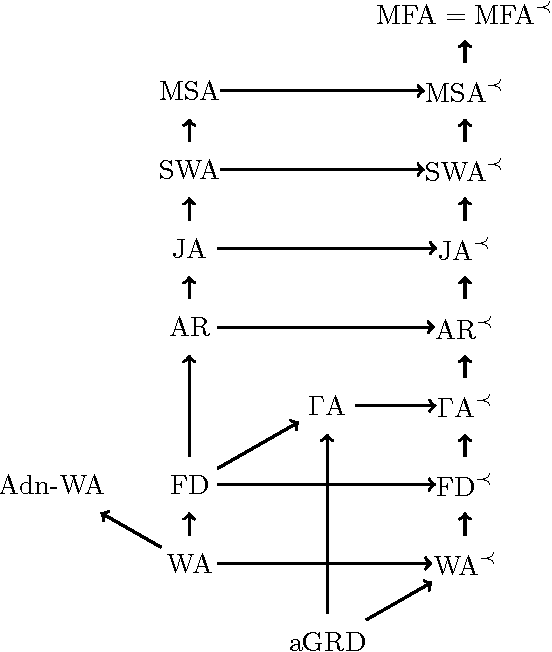
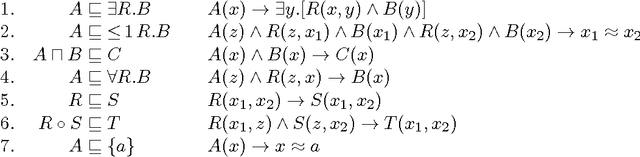
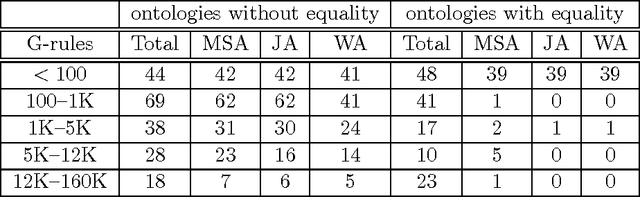
Answering conjunctive queries (CQs) over a set of facts extended with existential rules is a prominent problem in knowledge representation and databases. This problem can be solved using the chase algorithm, which extends the given set of facts with fresh facts in order to satisfy the rules. If the chase terminates, then CQs can be evaluated directly in the resulting set of facts. The chase, however, does not terminate necessarily, and checking whether the chase terminates on a given set of rules and facts is undecidable. Numerous acyclicity notions were proposed as sufficient conditions for chase termination. In this paper, we present two new acyclicity notions called model-faithful acyclicity (MFA) and model-summarising acyclicity (MSA). Furthermore, we investigate the landscape of the known acyclicity notions and establish a complete taxonomy of all notions known to us. Finally, we show that MFA and MSA generalise most of these notions. Existential rules are closely related to the Horn fragments of the OWL 2 ontology language; furthermore, several prominent OWL 2 reasoners implement CQ answering by using the chase to materialise all relevant facts. In order to avoid termination problems, many of these systems handle only the OWL 2 RL profile of OWL 2; furthermore, some systems go beyond OWL 2 RL, but without any termination guarantees. In this paper we also investigate whether various acyclicity notions can provide a principled and practical solution to these problems. On the theoretical side, we show that query answering for acyclic ontologies is of lower complexity than for general ontologies. On the practical side, we show that many of the commonly used OWL 2 ontologies are MSA, and that the number of facts obtained by materialisation is not too large. Our results thus suggest that principled development of materialisation-based OWL 2 reasoners is practically feasible.

Reasoning over Ontologies with Hidden Content: The Import-by-Query Approach

There is currently a growing interest in techniques for hiding parts of the signature of an ontology Kh that is being reused by another ontology Kv. Towards this goal, in this paper we propose the import-by-query framework, which makes the content of Kh accessible through a limited query interface. If Kv reuses the symbols from Kh in a certain restricted way, one can reason over Kv U Kh by accessing only Kv and the query interface. We map out the landscape of the import-by-query problem. In particular, we outline the limitations of our framework and prove that certain restrictions on the expressivity of Kh and the way in which Kv reuses symbols from Kh are strictly necessary to enable reasoning in our setting. We also identify cases in which reasoning is possible and we present suitable import-by-query reasoning algorithms.

Completeness Guarantees for Incomplete Ontology Reasoners: Theory and Practice

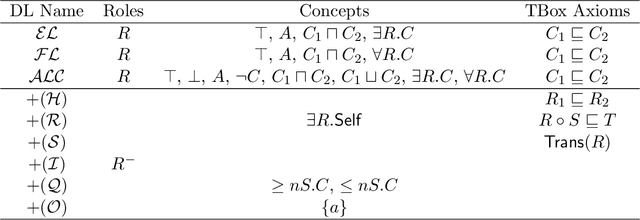
To achieve scalability of query answering, the developers of Semantic Web applications are often forced to use incomplete OWL 2 reasoners, which fail to derive all answers for at least one query, ontology, and data set. The lack of completeness guarantees, however, may be unacceptable for applications in areas such as health care and defence, where missing answers can adversely affect the applications functionality. Furthermore, even if an application can tolerate some level of incompleteness, it is often advantageous to estimate how many and what kind of answers are being lost. In this paper, we present a novel logic-based framework that allows one to check whether a reasoner is complete for a given query Q and ontology T---that is, whether the reasoner is guaranteed to compute all answers to Q w.r.t. T and an arbitrary data set A. Since ontologies and typical queries are often fixed at application design time, our approach allows application developers to check whether a reasoner known to be incomplete in general is actually complete for the kinds of input relevant for the application. We also present a technique that, given a query Q, an ontology T, and reasoners R_1 and R_2 that satisfy certain assumptions, can be used to determine whether, for each data set A, reasoner R_1 computes more answers to Q w.r.t. T and A than reasoner R_2. This allows application developers to select the reasoner that provides the highest degree of completeness for Q and T that is compatible with the applications scalability requirements. Our results thus provide a theoretical and practical foundation for the design of future ontology-based information systems that maximise scalability while minimising or even eliminating incompleteness of query answers.

Hypertableau Reasoning for Description Logics

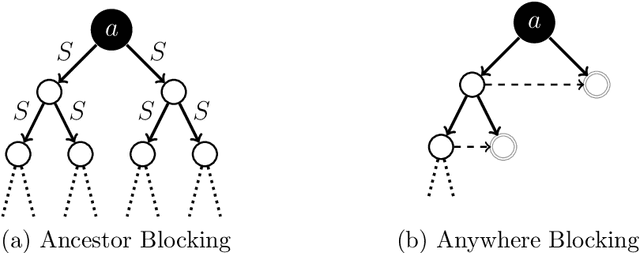
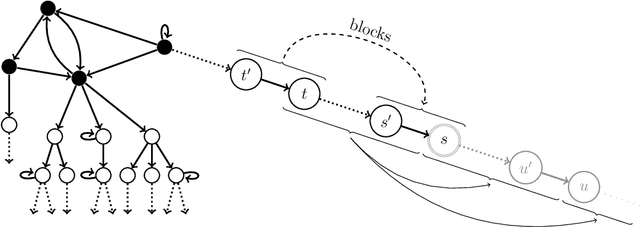
We present a novel reasoning calculus for the description logic SHOIQ^+---a knowledge representation formalism with applications in areas such as the Semantic Web. Unnecessary nondeterminism and the construction of large models are two primary sources of inefficiency in the tableau-based reasoning calculi used in state-of-the-art reasoners. In order to reduce nondeterminism, we base our calculus on hypertableau and hyperresolution calculi, which we extend with a blocking condition to ensure termination. In order to reduce the size of the constructed models, we introduce anywhere pairwise blocking. We also present an improved nominal introduction rule that ensures termination in the presence of nominals, inverse roles, and number restrictions---a combination of DL constructs that has proven notoriously difficult to handle. Our implementation shows significant performance improvements over state-of-the-art reasoners on several well-known ontologies.

Computing Datalog Rewritings beyond Horn Ontologies

Rewriting-based approaches for answering queries over an OWL 2 DL ontology have so far been developed mainly for Horn fragments of OWL 2 DL. In this paper, we study the possibilities of answering queries over non-Horn ontologies using datalog rewritings. We prove that this is impossible in general even for very simple ontology languages, and even if PTIME = NP. Furthermore, we present a resolution-based procedure for $\SHI$ ontologies that, in case it terminates, produces a datalog rewriting of the ontology. Our procedure necessarily terminates on DL-Lite_{bool}^H ontologies---an extension of OWL 2 QL with transitive roles and Boolean connectives.

Introducing Nominals to the Combined Query Answering Approaches for EL

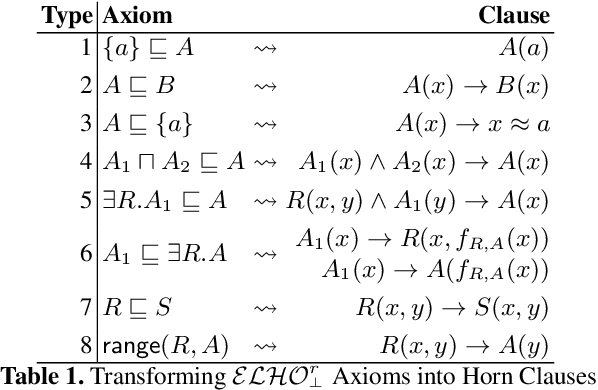
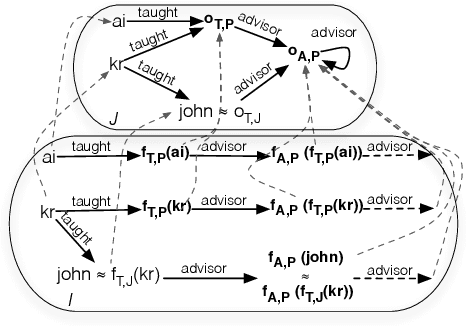
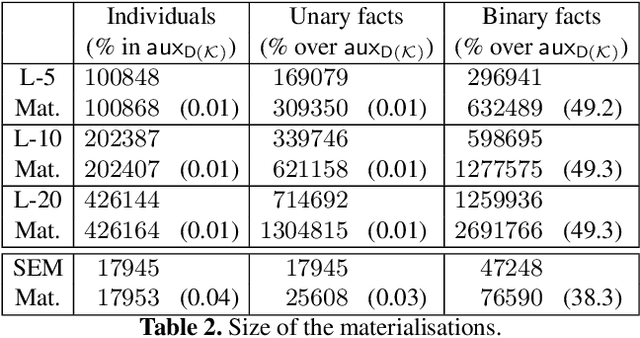
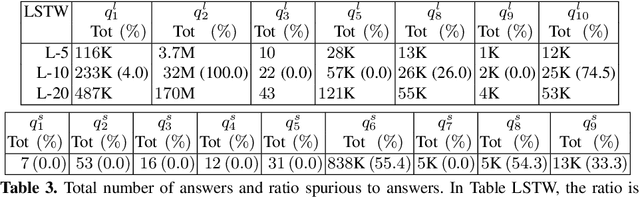
So-called combined approaches answer a conjunctive query over a description logic ontology in three steps: first, they materialise certain consequences of the ontology and the data; second, they evaluate the query over the data; and third, they filter the result of the second phase to eliminate unsound answers. Such approaches were developed for various members of the DL-Lite and the EL families of languages, but none of them can handle ontologies containing nominals. In our work, we bridge this gap and present a combined query answering approach for ELHO---a logic that contains all features of the OWL 2 EL standard apart from transitive roles and complex role inclusions. This extension is nontrivial because nominals require equality reasoning, which introduces complexity into the first and the third step. Our empirical evaluation suggests that our technique is suitable for practical application, and so it provides a practical basis for conjunctive query answering in a large fragment of OWL 2 EL.