Forward Only Learning for Orthogonal Neural Networks of any Depth

Backpropagation is still the de facto algorithm used today to train neural networks. With the exponential growth of recent architectures, the computational cost of this algorithm also becomes a burden. The recent PEPITA and forward-only frameworks have proposed promising alternatives, but they failed to scale up to a handful of hidden layers, yet limiting their use. In this paper, we first analyze theoretically the main limitations of these approaches. It allows us the design of a forward-only algorithm, which is equivalent to backpropagation under the linear and orthogonal assumptions. By relaxing the linear assumption, we then introduce FOTON (Forward-Only Training of Orthogonal Networks) that bridges the gap with the backpropagation algorithm. Experimental results show that it outperforms PEPITA, enabling us to train neural networks of any depth, without the need for a backward pass. Moreover its performance on convolutional networks clearly opens up avenues for its application to more advanced architectures. The code is open-sourced at https://github.com/p0lcAi/FOTON .

Bridging the Theoretical Gap in Randomized Smoothing

Randomized smoothing has become a leading approach for certifying adversarial robustness in machine learning models. However, a persistent gap remains between theoretical certified robustness and empirical robustness accuracy. This paper introduces a new framework that bridges this gap by leveraging Lipschitz continuity for certification and proposing a novel, less conservative method for computing confidence intervals in randomized smoothing. Our approach tightens the bounds of certified robustness, offering a more accurate reflection of model robustness in practice. Through rigorous experimentation we show that our method improves the robust accuracy, compressing the gap between empirical findings and previous theoretical results. We argue that investigating local Lipschitz constants and designing ad-hoc confidence intervals can further enhance the performance of randomized smoothing. These results pave the way for a deeper understanding of the relationship between Lipschitz continuity and certified robustness.

Conditional Distribution Quantization in Machine Learning

Conditional expectation \mathbb{E}(Y \mid X) often fails to capture the complexity of multimodal conditional distributions \mathcal{L}(Y \mid X). To address this, we propose using n-point conditional quantizations--functional mappings of X that are learnable via gradient descent--to approximate \mathcal{L}(Y \mid X). This approach adapts Competitive Learning Vector Quantization (CLVQ), tailored for conditional distributions. It goes beyond single-valued predictions by providing multiple representative points that better reflect multimodal structures. It enables the approximation of the true conditional law in the Wasserstein distance. The resulting framework is theoretically grounded and useful for uncertainty quantification and multimodal data generation tasks. For example, in computer vision inpainting tasks, multiple plausible reconstructions may exist for the same partially observed input image X. We demonstrate the effectiveness of our approach through experiments on synthetic and real-world datasets.

Accelerated Training through Iterative Gradient Propagation Along the Residual Path

Despite being the cornerstone of deep learning, backpropagation is criticized for its inherent sequentiality, which can limit the scalability of very deep models. Such models faced convergence issues due to vanishing gradient, later resolved using residual connections. Variants of these are now widely used in modern architecture. However, the computational cost of backpropagation remains a major burden, accounting for most of the training time. Taking advantage of residual-like architectural designs, we introduce Highway backpropagation, a parallelizable iterative algorithm that approximates backpropagation, by alternatively i) accumulating the gradient estimates along the residual path, and ii) backpropagating them through every layer in parallel. This algorithm is naturally derived from a decomposition of the gradient as the sum of gradients flowing through all paths and is adaptable to a diverse set of common architectures, ranging from ResNets and Transformers to recurrent neural networks. Through an extensive empirical study on a large selection of tasks and models, we evaluate Highway-BP and show that major speedups can be achieved with minimal performance degradation.

Chain and Causal Attention for Efficient Entity Tracking

This paper investigates the limitations of transformers for entity-tracking tasks in large language models. We identify a theoretical constraint, showing that transformers require at least $\log_2 (n+1)$ layers to handle entity tracking with $n$ state changes. To address this issue, we propose an efficient and frugal enhancement to the standard attention mechanism, enabling it to manage long-term dependencies more efficiently. By considering attention as an adjacency matrix, our model can track entity states with a single layer. Empirical results demonstrate significant improvements in entity tracking datasets while keeping competitive performance on standard natural language modeling. Our modified attention allows us to achieve the same performance with drastically fewer layers. Additionally, our enhanced mechanism reveals structured internal representations of attention. Extensive experiments on both toy and complex datasets validate our approach. Our contributions include theoretical insights, an improved attention mechanism, and empirical validation.

Spectral Norm of Convolutional Layers with Circular and Zero Paddings

This paper leverages the use of \emph{Gram iteration} an efficient, deterministic, and differentiable method for computing spectral norm with an upper bound guarantee. Designed for circular convolutional layers, we generalize the use of the Gram iteration to zero padding convolutional layers and prove its quadratic convergence. We also provide theorems for bridging the gap between circular and zero padding convolution's spectral norm. We design a \emph{spectral rescaling} that can be used as a competitive $1$-Lipschitz layer that enhances network robustness. Demonstrated through experiments, our method outperforms state-of-the-art techniques in precision, computational cost, and scalability. The code of experiments is available at https://github.com/blaisedelattre/lip4conv.

The Lipschitz-Variance-Margin Tradeoff for Enhanced Randomized Smoothing

Real-life applications of deep neural networks are hindered by their unsteady predictions when faced with noisy inputs and adversarial attacks. The certified radius is in this context a crucial indicator of the robustness of models. However how to design an efficient classifier with a sufficient certified radius? Randomized smoothing provides a promising framework by relying on noise injection in inputs to obtain a smoothed and more robust classifier. In this paper, we first show that the variance introduced by randomized smoothing closely interacts with two other important properties of the classifier, i.e. its Lipschitz constant and margin. More precisely, our work emphasizes the dual impact of the Lipschitz constant of the base classifier, on both the smoothed classifier and the empirical variance. Moreover, to increase the certified robust radius, we introduce a different simplex projection technique for the base classifier to leverage the variance-margin trade-off thanks to Bernstein's concentration inequality, along with an enhanced Lipschitz bound. Experimental results show a significant improvement in certified accuracy compared to current state-of-the-art methods. Our novel certification procedure allows us to use pre-trained models that are used with randomized smoothing, effectively improving the current certification radius in a zero-shot manner.

Efficient Bound of Lipschitz Constant for Convolutional Layers by Gram Iteration

Since the control of the Lipschitz constant has a great impact on the training stability, generalization, and robustness of neural networks, the estimation of this value is nowadays a real scientific challenge. In this paper we introduce a precise, fast, and differentiable upper bound for the spectral norm of convolutional layers using circulant matrix theory and a new alternative to the Power iteration. Called the Gram iteration, our approach exhibits a superlinear convergence. First, we show through a comprehensive set of experiments that our approach outperforms other state-of-the-art methods in terms of precision, computational cost, and scalability. Then, it proves highly effective for the Lipschitz regularization of convolutional neural networks, with competitive results against concurrent approaches. Code is available at https://github.com/blaisedelattre/lip4conv.

A Unified Algebraic Perspective on Lipschitz Neural Networks

Important research efforts have focused on the design and training of neural networks with a controlled Lipschitz constant. The goal is to increase and sometimes guarantee the robustness against adversarial attacks. Recent promising techniques draw inspirations from different backgrounds to design 1-Lipschitz neural networks, just to name a few: convex potential layers derive from the discretization of continuous dynamical systems, Almost-Orthogonal-Layer proposes a tailored method for matrix rescaling. However, it is today important to consider the recent and promising contributions in the field under a common theoretical lens to better design new and improved layers. This paper introduces a novel algebraic perspective unifying various types of 1-Lipschitz neural networks, including the ones previously mentioned, along with methods based on orthogonality and spectral methods. Interestingly, we show that many existing techniques can be derived and generalized via finding analytical solutions of a common semidefinite programming (SDP) condition. We also prove that AOL biases the scaled weight to the ones which are close to the set of orthogonal matrices in a certain mathematical manner. Moreover, our algebraic condition, combined with the Gershgorin circle theorem, readily leads to new and diverse parameterizations for 1-Lipschitz network layers. Our approach, called SDP-based Lipschitz Layers (SLL), allows us to design non-trivial yet efficient generalization of convex potential layers. Finally, the comprehensive set of experiments on image classification shows that SLLs outperform previous approaches on certified robust accuracy. Code is available at https://github.com/araujoalexandre/Lipschitz-SLL-Networks.

Scalable Lipschitz Residual Networks with Convex Potential Flows

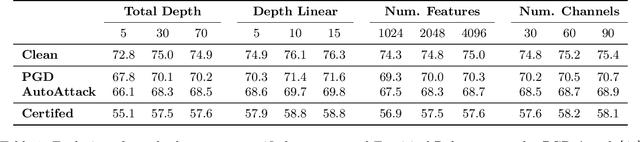
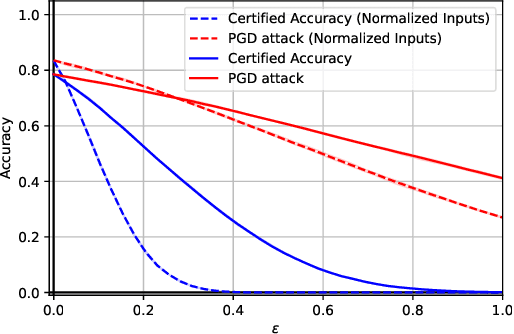
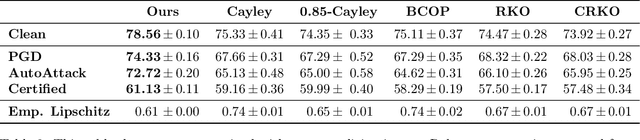
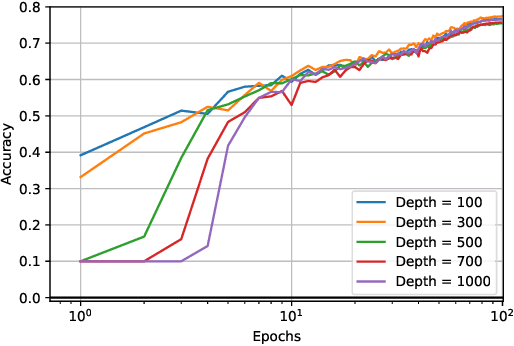
The Lipschitz constant of neural networks has been established as a key property to enforce the robustness of neural networks to adversarial examples. However, recent attempts to build $1$-Lipschitz Neural Networks have all shown limitations and robustness have to be traded for accuracy and scalability or vice versa. In this work, we first show that using convex potentials in a residual network gradient flow provides a built-in $1$-Lipschitz transformation. From this insight, we leverage the work on Input Convex Neural Networks to parametrize efficient layers with this property. A comprehensive set of experiments on CIFAR-10 demonstrates the scalability of our architecture and the benefit of our approach for $\ell_2$ provable defenses. Indeed, we train very deep and wide neural networks (up to $1000$ layers) and reach state-of-the-art results in terms of standard and certified accuracy, along with empirical robustness, in comparison with other $1$-Lipschitz architectures.