Reconstruction of Graph Signals on Complex Manifolds with Kernel Methods

Graph signals are widely used to describe vertex attributes or features in graph-structured data, with applications spanning the internet, social media, transportation, sensor networks, and biomedicine. Graph signal processing (GSP) has emerged to facilitate the analysis, processing, and sampling of such signals. While kernel methods have been extensively studied for estimating graph signals from samples provided on a subset of vertices, their application to complex-valued graph signals remains largely unexplored. This paper introduces a novel framework for reconstructing graph signals using kernel methods on complex manifolds. By embedding graph vertices into a higher-dimensional complex ambient space that approximates a lower-dimensional manifold, the framework extends the reproducing kernel Hilbert space to complex manifolds. It leverages Hermitian metrics and geometric measures to characterize kernels and graph signals. Additionally, several traditional kernels and graph topology-driven kernels are proposed for reconstructing complex graph signals. Finally, experimental results on synthetic and real-world datasets demonstrate the effectiveness of this framework in accurately reconstructing complex graph signals, outperforming conventional kernel-based approaches. This work lays a foundational basis for integrating complex geometry and kernel methods in GSP.

Discrete Linear Canonical Transform on Graphs

With the wide application of spectral and algebraic theory in discrete signal processing techniques in the field of graph signal processing, an increasing number of signal processing methods have been proposed, such as the graph Fourier transform, graph wavelet transform and windowed graph Fourier transform. In this paper, we propose and design the definition of the discrete linear canonical transform on graphs (GLCT), which is an extension of the discrete linear canonical transform (DLCT), just as the graph Fourier transform (GFT) is an extension of the discrete Fourier transform (DFT). First, based on the centrality and scalability of the DLCT eigendecomposition approach, the definition of GLCT is proposed by combining graph chirp-Fourier transform, graph scale transform and graph fractional Fourier transform. Second, we derive and discuss the properties and special cases of GLCT. Finally, some GLCT examples of the graph signals are given to illustrate the improvement of the transformation.

The two-dimensional OLCT of angularly periodic functions in polar coordinates

The two-dimensional (2D) offset linear canonical transform (OLCT) in polar coordinates plays an important role in many fields of optics and signal processing. This paper studies the 2D OLCT in polar coordinates. Firstly, we extend the 2D OLCT to the polar coordinate system, and obtain the offset linear canonical Hankel transform (OLCHT) formula. Secondly, through the angular periodic function with a period of 2{\pi}, the relationship between the 2D OLCT and the OLCHT is revealed. Finally, the spatial shift and convolution theorems for the 2D OLCT are proposed by using this relationship.

A Novel Reconstruction Algorithm based on Fractional Fourier Transform for Unlimited Sampling

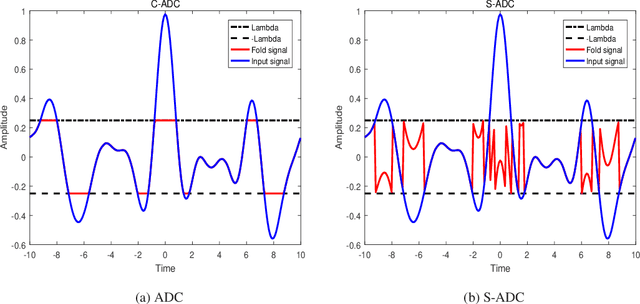
The recovery of bandlimited signals with high dynamic range is a hot issue in sampling research. The unlimited sampling theory expands the recordable range of traditional analog-to-digital converters (ADCs) arbitrarily, and the signal is folded back into a low dynamic range measurement, avoiding the saturation problem. We study the unlimited sampling problem of high dynamic nonbandlimited signals in the Fourier domain (FD) based on the fractional Fourier transform (FRFT). First, the modular nonlinear folding is performed in the fractional Fourier domain (FRFD) for modular arithmetic. Then, the fractional spectrum is estimated for any folding time by means of annihilation filtering. Finally, a novel unlimited sampling algorithm in the FRFD is obtained. The results show that the non-bandlimited signal can be reconstructed in the FD based on the FRFT, and it is not affected by the ADC threshold.

Multi-dimensional graph fractional Fourier transform and its application

Many multi-dimensional signals appear in the real world, such as digital images and data that has spatial and temporal dimensions. How to show the spectrum of these multi-dimensional signals correctly is a key challenge in the field of graph signal processing. This paper investigates the novel transform for multi-dimensional signals defined on Cartesian product graph and studies several related properties. Our work includes: (i) defining the multi-dimensional graph fractional Fourier transform (MGFRFT) based on Laplacian matrix and adjacency matrix; (ii) exploring the advantages of MGFRFT in processing multi-dimensional signals in terms of spectrum and computational time; (iii) applying the proposed transform to data compression to highlight the utility and effectiveness of it.