Subspace Representation Learning for Sparse Linear Arrays to Localize More Sources than Sensors: A Deep Learning Methodology

Localizing more sources than sensors with a sparse linear array (SLA) has long relied on minimizing a distance between two covariance matrices and recent algorithms often utilize semidefinite programming (SDP). Although deep neural network (DNN)-based methods offer new alternatives, they still depend on covariance matrix fitting. In this paper, we develop a novel methodology that estimates the co-array subspaces from a sample covariance for SLAs. Our methodology trains a DNN to learn signal and noise subspace representations that are invariant to the selection of bases. To learn such representations, we propose loss functions that gauge the separation between the desired and the estimated subspace. In particular, we propose losses that measure the length of the shortest path between subspaces viewed on a union of Grassmannians, and prove that it is possible for a DNN to approximate signal subspaces. The computation of learning subspaces of different dimensions is accelerated by a new batch sampling strategy called consistent rank sampling. The methodology is robust to array imperfections due to its geometry-agnostic and data-driven nature. In addition, we propose a fully end-to-end gridless approach that directly learns angles to study the possibility of bypassing subspace methods. Numerical results show that learning such subspace representations is more beneficial than learning covariances or angles. It outperforms conventional SDP-based methods such as the sparse and parametric approach (SPA) and existing DNN-based covariance reconstruction methods for a wide range of signal-to-noise ratios (SNRs), snapshots, and source numbers for both perfect and imperfect arrays.

Novel Active Sensing and Inference for mmWave Beam Alignment Using Single RF Chain Systems

We propose a novel sensing approach for the beam alignment problem in millimeter wave systems using a single Radio Frequency (RF) chain. Conventionally, beam alignment using a single phased array involves comparing beamformer output power across different spatial regions. This incurs large training overhead due to the need to perform the beam scan operation. The proposed Synthesis of Virtual Array Manifold (SVAM) sensing methodology is inspired from synthetic aperture radar systems and realizes a virtual array geometry over temporal measurements. We demonstrate the benefits of SVAM using Cram\'er-Rao bound (CRB) analysis over schemes that repeat beam pattern to boost signal-to-noise (SNR) ratio. We also showcase versatile applicability of the proposed SVAM sensing by incorporating it within existing beam alignment procedures that assume perfect knowledge of the small-scale fading coefficient. We further consider the practical scenario wherein we estimate the fading coefficient and propose a novel beam alignment procedure based on efficient computation of an approximate posterior density on dominant path angle. We provide numerical experiments to study the impact of parameters involved in the procedure. The performance of the proposed sensing and beam alignment algorithm is empirically observed to approach the fading coefficient-perfectly known performance, even at low SNR.

Regularized Neural Detection for One-Bit Massive MIMO Communication Systems

Detection for one-bit massive MIMO systems presents several challenges especially for higher order constellations. Recent advances in both model-based analysis and deep learning frameworks have resulted in several robust one-bit detector designs. Our work builds on the current state-of-the-art gradient descent (GD)-based detector. We introduce two novel contributions in our detector design: (i) We augment each GD iteration with a deep learning-aided regularization step, and (ii) We introduce a novel constellation-based loss function for our regularized DNN detector. This one-bit detection strategy is applied to two different DNN architectures based on algorithm unrolling, namely, a deep unfolded neural network and a deep recurrent neural network. Being trained on multiple randomly sampled channel matrices, these networks are developed as general one-bit detectors. The numerical results show that the combination of the DNN-augmented regularized GD and constellation-based loss function improve the quality of our one-bit detector, especially for higher order M-QAM constellations.

A DNN based Normalized Time-frequency Weighted Criterion for Robust Wideband DoA Estimation

Deep neural networks (DNNs) have greatly benefited direction of arrival (DoA) estimation methods for speech source localization in noisy environments. However, their localization accuracy is still far from satisfactory due to the vulnerability to nonspeech interference. To improve the robustness against interference, we propose a DNN based normalized time-frequency (T-F) weighted criterion which minimizes the distance between the candidate steering vectors and the filtered snapshots in the T-F domain. Our method requires no eigendecomposition and uses a simple normalization to prevent the optimization objective from being misled by noisy filtered snapshots. We also study different designs of T-F weights guided by a DNN. We find that duplicating the Hadamard product of speech ratio masks is highly effective and better than other techniques such as direct masking and taking the mean in the proposed approach. However, the best-performing design of T-F weights is criterion-dependent in general. Experiments show that the proposed method outperforms popular DNN based DoA estimation methods including widely used subspace methods in noisy and reverberant environments.

Vector Quantization Methods for Access Point Placement in Cell-Free Massive MIMO Systems

We examine the problem of uplink cell-free access point (AP) placement in the context of optimal throughput. In this regard, we formulate two main placement problems, namely the sum rate and minimum rate maximization problems, and discuss the challenges associated with solving the underlying optimization problem with the help of some simple scenarios. As a practical solution to the AP placement problem, we suggest a vector quantization (VQ) approach. The suitability of the VQ approach to cell-free AP placement is investigated by examining three VQ-based solutions. First, the standard VQ approach, that is the Lloyd algorithm (using the squared error distortion function) is described. Second, the tree-structured VQ (TSVQ), which performs successive partitioning of the distribution space is applied. Third, a probability density function optimized VQ (PDFVQ) procedure is outlined, which enables efficient, low complexity, and scalable placement, and is aimed at a massive distributed multiple-input-multiple-output (MIMO) scenario. While the VQ-based solutions do not solve the cell-free AP placement problems explicitly, numerical experiments show that their sum and minimum rate performances are good enough, and offer a good starting point for gradient-based optimization methods. Among the VQ solutions, PDFVQ, with advantages over the other VQ methods, offers a good trade-off between sum and minimum rates.

Improved Bounds on Neural Complexity for Representing Piecewise Linear Functions

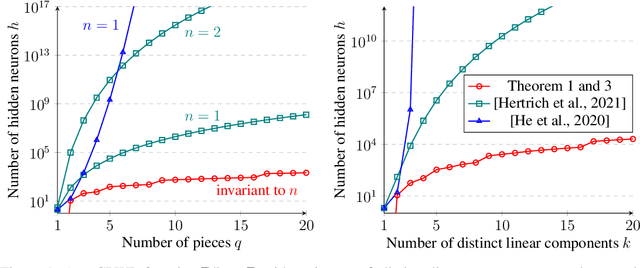
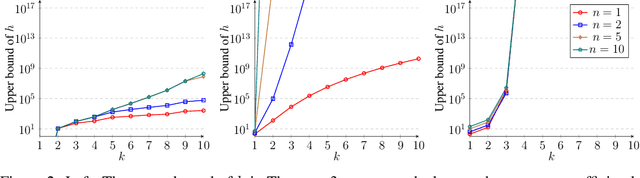
A deep neural network using rectified linear units represents a continuous piecewise linear (CPWL) function and vice versa. Recent results in the literature estimated that the number of neurons needed to exactly represent any CPWL function grows exponentially with the number of pieces or exponentially in terms of the factorial of the number of distinct linear components. Moreover, such growth is amplified linearly with the input dimension. These existing results seem to indicate that the cost of representing a CPWL function is expensive. In this paper, we propose much tighter bounds and establish a polynomial time algorithm to find a network satisfying these bounds for any given CPWL function. We prove that the number of hidden neurons required to exactly represent any CPWL function is at most a quadratic function of the number of pieces. In contrast to all previous results, this upper bound is invariant to the input dimension. Besides the number of pieces, we also study the number of distinct linear components in CPWL functions. When such a number is also given, we prove that the quadratic complexity turns into bilinear, which implies a lower neural complexity because the number of distinct linear components is always not greater than the minimum number of pieces in a CPWL function. When the number of pieces is unknown, we prove that, in terms of the number of distinct linear components, the neural complexity of any CPWL function is at most polynomial growth for low-dimensional inputs and a factorial growth for the worst-case scenario, which are significantly better than existing results in the literature.

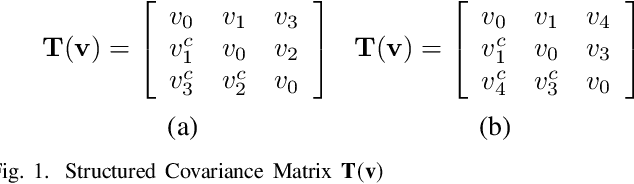
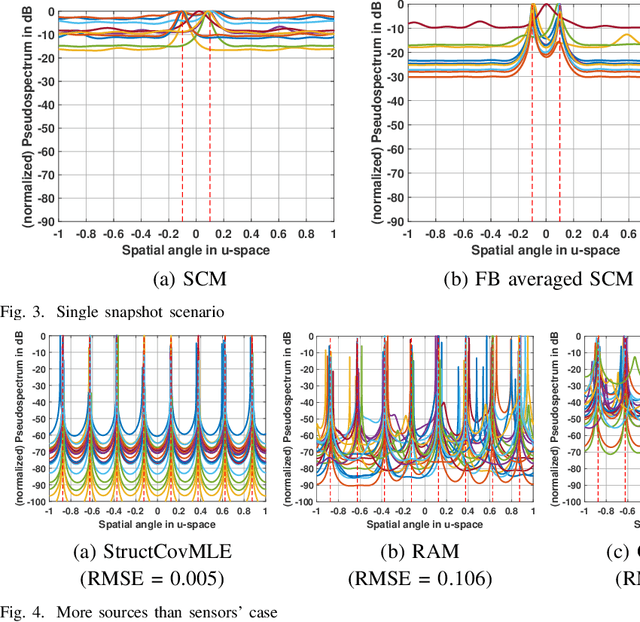
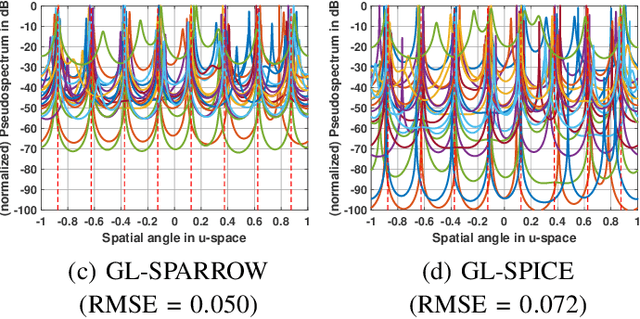
Maximum Likelihood-based Gridless DoA Estimation Using Structured Covariance Matrix Recovery and SBL with Grid Refinement

We consider the parametric data model employed in applications such as line spectral estimation and direction-of-arrival estimation. We focus on the stochastic maximum likelihood estimation (MLE) framework and offer approaches to estimate the parameter of interest in a gridless manner, overcoming the model complexities of the past. This progress is enabled by the modern trend of reparameterization of the objective and exploiting the sparse Bayesian learning (SBL) approach. The latter is shown to be a correlation-aware method, and for the underlying problem it is identified as a grid-based technique for recovering a structured covariance matrix of the measurements. For the case when the structured matrix is expressible as a sampled Toeplitz matrix, such as when measurements are sampled in time or space at regular intervals, additional constraints and reparameterization of the SBL objective leads to the proposed structured matrix recovery technique based on MLE. The proposed optimization problem is non-convex, and we propose a majorization-minimization based iterative procedure to estimate the structured matrix; each iteration solves a semidefinite program. We recover the parameter of interest in a gridless manner by appealing to the Caratheodory-Fejer result on decomposition of PSD Toeplitz matrices. For the general case of irregularly spaced time or spatial samples, we propose an iterative SBL procedure that refines grid points to increase resolution near potential source locations, while maintaining a low per iteration complexity. We provide numerical results to evaluate and compare the performance of the proposed techniques with other gridless techniques, and the CRB. The proposed correlation-aware approach is more robust to environmental/system effects such as low number of snapshots, correlated sources, small separation between source locations and improves sources identifiability.

A Generalized Proportionate-Type Normalized Subband Adaptive Filter

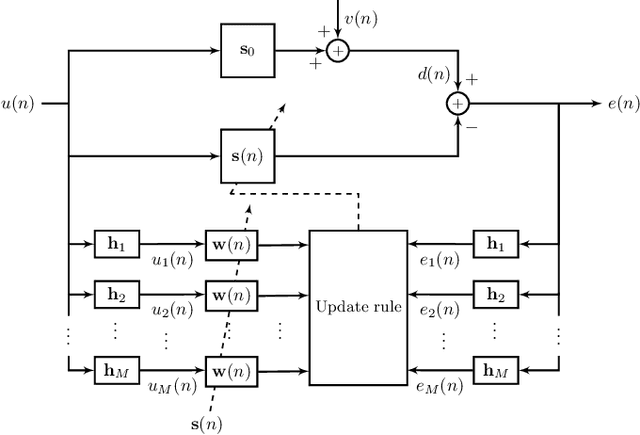
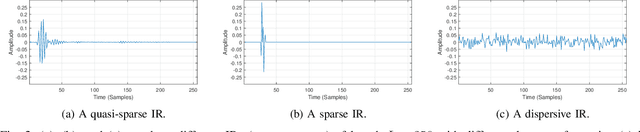
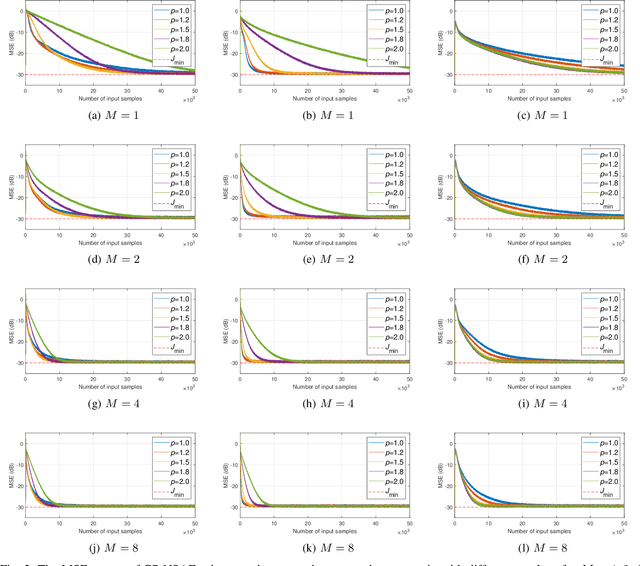
We show that a new design criterion, i.e., the least squares on subband errors regularized by a weighted norm, can be used to generalize the proportionate-type normalized subband adaptive filtering (PtNSAF) framework. The new criterion directly penalizes subband errors and includes a sparsity penalty term which is minimized using the damped regularized Newton's method. The impact of the proposed generalized PtNSAF (GPtNSAF) is studied for the system identification problem via computer simulations. Specifically, we study the effects of using different numbers of subbands and various sparsity penalty terms for quasi-sparse, sparse, and dispersive systems. The results show that the benefit of increasing the number of subbands is larger than promoting sparsity of the estimated filter coefficients when the target system is quasi-sparse or dispersive. On the other hand, for sparse target systems, promoting sparsity becomes more important. More importantly, the two aspects provide complementary and additive benefits to the GPtNSAF for speeding up convergence.

ResNEsts and DenseNEsts: Block-based DNN Models with Improved Representation Guarantees

Models recently used in the literature proving residual networks (ResNets) are better than linear predictors are actually different from standard ResNets that have been widely used in computer vision. In addition to the assumptions such as scalar-valued output or single residual block, these models have no nonlinearities at the final residual representation that feeds into the final affine layer. To codify such a difference in nonlinearities and reveal a linear estimation property, we define ResNEsts, i.e., Residual Nonlinear Estimators, by simply dropping nonlinearities at the last residual representation from standard ResNets. We show that wide ResNEsts with bottleneck blocks can always guarantee a very desirable training property that standard ResNets aim to achieve, i.e., adding more blocks does not decrease performance given the same set of basis elements. To prove that, we first recognize ResNEsts are basis function models that are limited by a coupling problem in basis learning and linear prediction. Then, to decouple prediction weights from basis learning, we construct a special architecture termed augmented ResNEst (A-ResNEst) that always guarantees no worse performance with the addition of a block. As a result, such an A-ResNEst establishes empirical risk lower bounds for a ResNEst using corresponding bases. Our results demonstrate ResNEsts indeed have a problem of diminishing feature reuse; however, it can be avoided by sufficiently expanding or widening the input space, leading to the above-mentioned desirable property. Inspired by the DenseNets that have been shown to outperform ResNets, we also propose a corresponding new model called Densely connected Nonlinear Estimator (DenseNEst). We show that any DenseNEst can be represented as a wide ResNEst with bottleneck blocks. Unlike ResNEsts, DenseNEsts exhibit the desirable property without any special architectural re-design.

A Novel Bayesian Approach for the Two-Dimensional Harmonic Retrieval Problem

Sparse signal recovery algorithms like sparse Bayesian learning work well but the complexity quickly grows when tackling higher dimensional parametric dictionaries. In this work we propose a novel Bayesian strategy to address the two dimensional harmonic retrieval problem, through remodeling and reparameterization of the standard data model. This new model allows us to introduce a block sparsity structure in a manner that enables a natural pairing of the parameters in the two dimensions. The numerical simulations demonstrate that the inference algorithm developed (H-MSBL) does not suffer from source identifiability issues and is capable of estimating the harmonic components in challenging scenarios, while maintaining a low computational complexity.