On Fast Johnson-Lindenstrauss Embeddings of Compact Submanifolds of $\mathbb{R}^N$ with Boundary

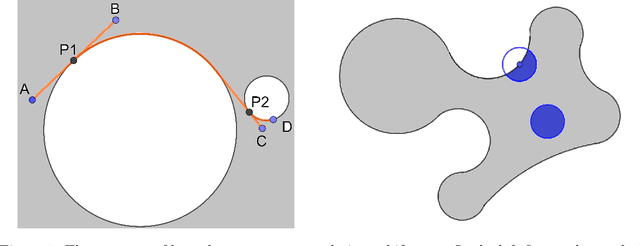
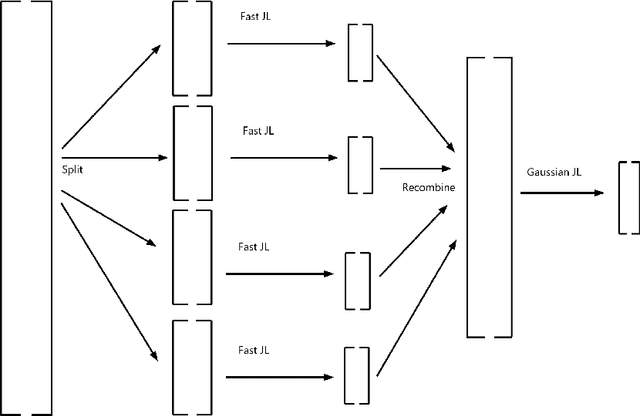
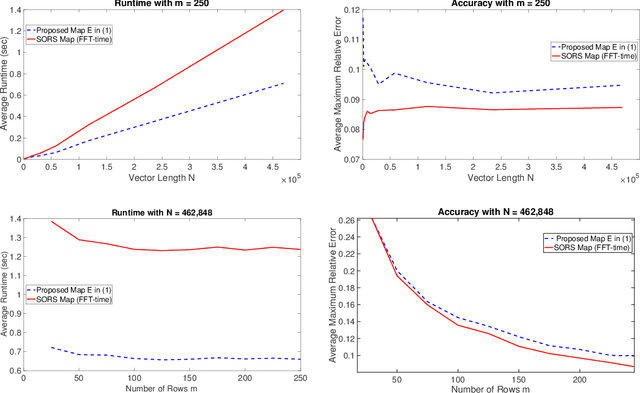
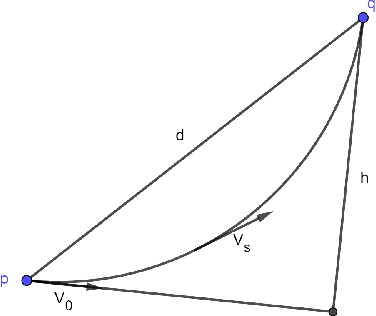
Let $\mathcal{M}$ be a smooth $d$-dimensional submanifold of $\mathbb{R}^N$ with boundary that's equipped with the Euclidean (chordal) metric, and choose $m \leq N$. In this paper we consider the probability that a random matrix $A \in \mathbb{R}^{m \times N}$ will serve as a bi-Lipschitz function $A: \mathcal{M} \rightarrow \mathbb{R}^m$ with bi-Lipschitz constants close to one for three different types of distributions on the $m \times N$ matrices $A$, including two whose realizations are guaranteed to have fast matrix-vector multiplies. In doing so we generalize prior randomized metric space embedding results of this type for submanifolds of $\mathbb{R}^N$ by allowing for the presence of boundary while also retaining, and in some cases improving, prior lower bounds on the achievable embedding dimensions $m$ for which one can expect small distortion with high probability. In particular, motivated by recent modewise embedding constructions for tensor data, herein we present a new class of highly structured distributions on matrices which outperform prior structured matrix distributions for embedding sufficiently low-dimensional submanifolds of $\mathbb{R}^N$ (with $d \lesssim \sqrt{N}$) with respect to both achievable embedding dimension, and computationally efficient realizations. As a consequence we are able to present, for example, a general new class of Johnson-Lindenstrauss embedding matrices for $\mathcal{O}(\log^c N)$-dimensional submanifolds of $\mathbb{R}^N$ which enjoy $\mathcal{O}(N \log (\log N))$-time matrix vector multiplications.

The Autonomous Racing Software Stack of the KIT19d

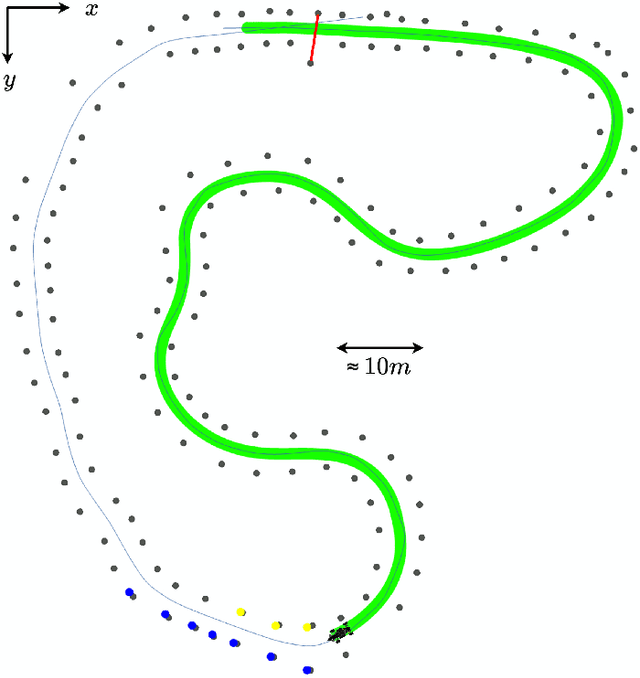
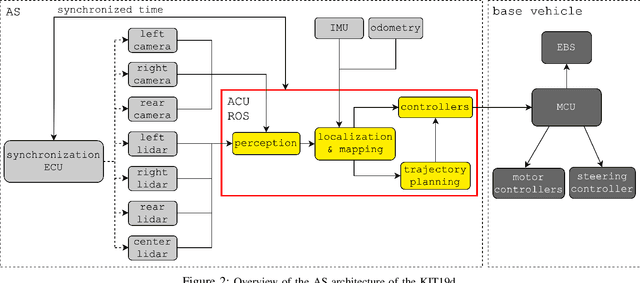
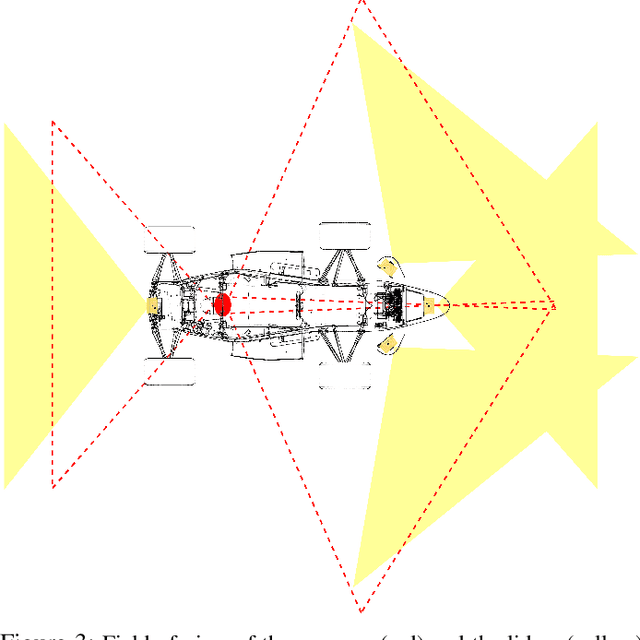
Formula Student Driverless challenges engineering students to develop autonomous single-seater race cars in a quest to bring about more graduates who are well-prepared to solve the real world problems associated with autonomous driving. In this paper, we present the software stack of KA-RaceIng's entry to the 2019 competitions. We cover the essential modules of the system, including perception, localization, mapping, motion planning, and control. Furthermore, development methods are outlined and an overview of the system architecture is given. We conclude by presenting selected runtime measurements, data logs, and competition results to provide an insight into the performance of the final prototype.