Exact Recovery Guarantees for Parameterized Non-linear System Identification Problem under Adversarial Attacks

In this work, we study the system identification problem for parameterized non-linear systems using basis functions under adversarial attacks. Motivated by the LASSO-type estimators, we analyze the exact recovery property of a non-smooth estimator, which is generated by solving an embedded $\ell_1$-loss minimization problem. First, we derive necessary and sufficient conditions for the well-specifiedness of the estimator and the uniqueness of global solutions to the underlying optimization problem. Next, we provide exact recovery guarantees for the estimator under two different scenarios of boundedness and Lipschitz continuity of the basis functions. The non-asymptotic exact recovery is guaranteed with high probability, even when there are more severely corrupted data than clean data. Finally, we numerically illustrate the validity of our theory. This is the first study on the sample complexity analysis of a non-smooth estimator for the non-linear system identification problem.

Exact Recovery for System Identification with More Corrupt Data than Clean Data

In this paper, we study the system identification problem for linear discrete-time systems under adversaries and analyze two lasso-type estimators. We study both asymptotic and non-asymptotic properties of these estimators in two separate scenarios, corresponding to deterministic and stochastic models for the attack times. Since the samples collected from the system are correlated, the existing results on lasso are not applicable. We show that when the system is stable and the attacks are injected periodically, the sample complexity for the exact recovery of the system dynamics is O(n), where n is the dimension of the states. When the adversarial attacks occur at each time instance with probability p, the required sample complexity for the exact recovery scales as O(\log(n)p/(1-p)^2). This result implies the almost sure convergence to the true system dynamics under the asymptotic regime. As a by-product, even when more than half of the data is compromised, our estimators still learn the system correctly. This paper provides the first mathematical guarantee in the literature on learning from correlated data for dynamical systems in the case when there is less clean data than corrupt data.

Semidefinite Programming versus Burer-Monteiro Factorization for Matrix Sensing

Many fundamental low-rank optimization problems, such as matrix completion, phase synchronization/retrieval, power system state estimation, and robust PCA, can be formulated as the matrix sensing problem. Two main approaches for solving matrix sensing are based on semidefinite programming (SDP) and Burer-Monteiro (B-M) factorization. The SDP method suffers from high computational and space complexities, whereas the B-M method may return a spurious solution due to the non-convexity of the problem. The existing theoretical guarantees for the success of these methods have led to similar conservative conditions, which may wrongly imply that these methods have comparable performances. In this paper, we shed light on some major differences between these two methods. First, we present a class of structured matrix completion problems for which the B-M methods fail with an overwhelming probability, while the SDP method works correctly. Second, we identify a class of highly sparse matrix completion problems for which the B-M method works and the SDP method fails. Third, we prove that although the B-M method exhibits the same performance independent of the rank of the unknown solution, the success of the SDP method is correlated to the rank of the solution and improves as the rank increases. Unlike the existing literature that has mainly focused on those instances of matrix sensing for which both SDP and B-M work, this paper offers the first result on the unique merit of each method over the alternative approach.

Factorization Approach for Low-complexity Matrix Completion Problems: Exponential Number of Spurious Solutions and Failure of Gradient Methods

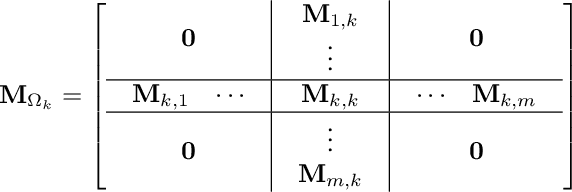
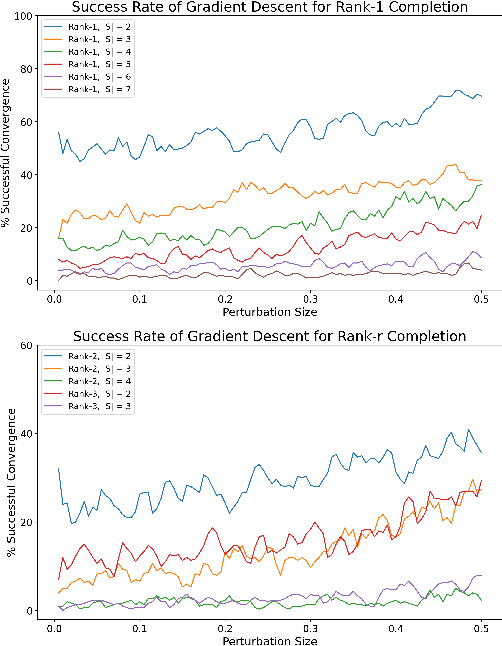
It is well-known that the Burer-Monteiro (B-M) factorization approach can efficiently solve low-rank matrix optimization problems under the RIP condition. It is natural to ask whether B-M factorization-based methods can succeed on any low-rank matrix optimization problems with a low information-theoretic complexity, i.e., polynomial-time solvable problems that have a unique solution. In this work, we provide a negative answer to the above question. We investigate the landscape of B-M factorized polynomial-time solvable matrix completion (MC) problems, which are the most popular subclass of low-rank matrix optimization problems without the RIP condition. We construct an instance of polynomial-time solvable MC problems with exponentially many spurious local minima, which leads to the failure of most gradient-based methods. Based on those results, we define a new complexity metric that potentially measures the solvability of low-rank matrix optimization problems based on the B-M factorization approach. In addition, we show that more measurements of the ground truth matrix can deteriorate the landscape, which further reveals the unfavorable behavior of the B-M factorization on general low-rank matrix optimization problems.