Finite-sample guarantees for data-driven forward-backward operator methods

We establish finite sample certificates on the quality of solutions produced by data-based forward-backward (FB) operator splitting schemes. As frequently happens in stochastic regimes, we consider the problem of finding a zero of the sum of two operators, where one is either unavailable in closed form or computationally expensive to evaluate, and shall therefore be approximated using a finite number of noisy oracle samples. Under the lens of algorithmic stability, we then derive probabilistic bounds on the distance between a true zero and the FB output without making specific assumptions about the underlying data distribution. We show that under weaker conditions ensuring the convergence of FB schemes, stability bounds grow proportionally to the number of iterations. Conversely, stronger assumptions yield stability guarantees that are independent of the iteration count. We then specialize our results to a popular FB stochastic Nash equilibrium seeking algorithm and validate our theoretical bounds on a control problem for smart grids, where the energy price uncertainty is approximated by means of historical data.

Generative Adversarial Networks as stochastic Nash games

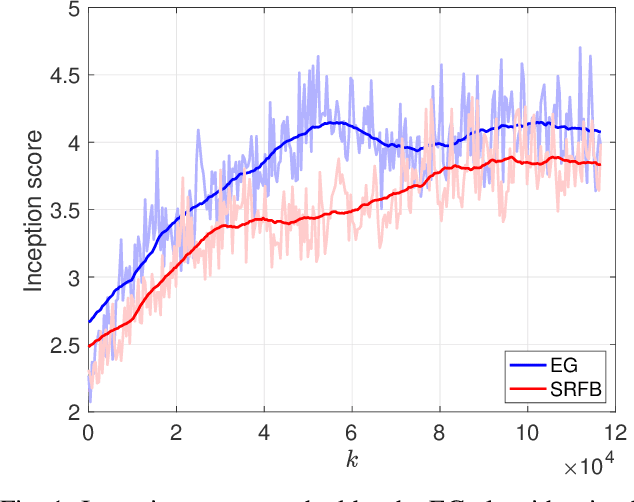
Generative adversarial networks (GANs) are a class of generative models with two antagonistic neural networks: the generator and the discriminator. These two neural networks compete against each other through an adversarial process that can be modelled as a stochastic Nash equilibrium problem. Since the associated training process is challenging, it is fundamental to design reliable algorithms to compute an equilibrium. In this paper, we propose a stochastic relaxed forward-backward algorithm for GANs and we show convergence to an exact solution or to a neighbourhood of it, if the pseudogradient mapping of the game is monotone. We apply our algorithm to the image generation problem where we observe computational advantages with respect to the extragradient scheme.

A game-theoretic approach for Generative Adversarial Networks

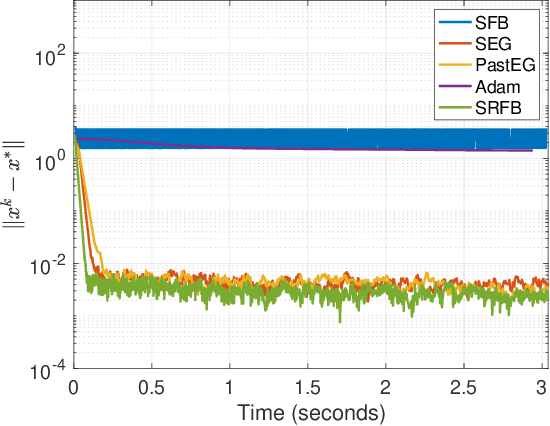
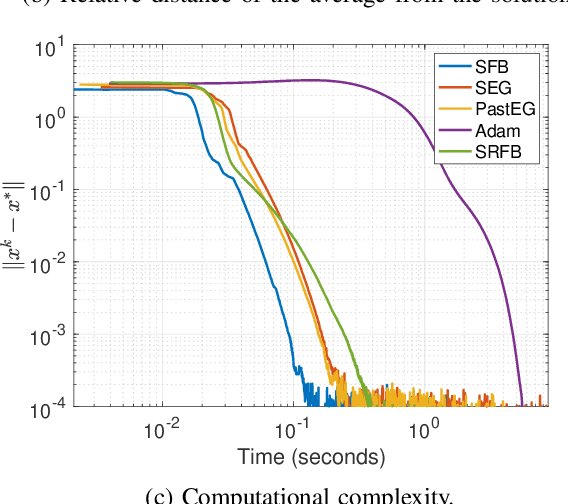
Generative adversarial networks (GANs) are a class of generative models, known for producing accurate samples. The key feature of GANs is that there are two antagonistic neural networks: the generator and the discriminator. The main bottleneck for their implementation is that the neural networks are very hard to train. One way to improve their performance is to design reliable algorithms for the adversarial process. Since the training can be cast as a stochastic Nash equilibrium problem, we rewrite it as a variational inequality and introduce an algorithm to compute an approximate solution. Specifically, we propose a stochastic relaxed forward-backward algorithm for GANs. We prove that when the pseudogradient mapping of the game is monotone, we have convergence to an exact solution or in a neighbourhood of it.