Neural Ordinary Differential Equation based Recurrent Neural Network Model

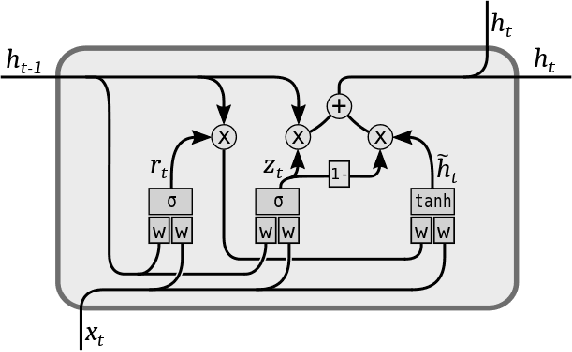
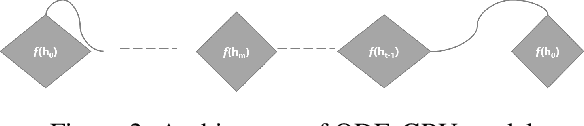
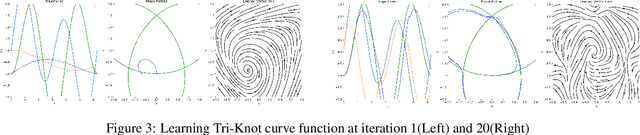
Neural differential equations are a promising new member in the neural network family. They show the potential of differential equations for time series data analysis. In this paper, the strength of the ordinary differential equation (ODE) is explored with a new extension. The main goal of this work is to answer the following questions: (i)~can ODE be used to redefine the existing neural network model? (ii)~can Neural ODEs solve the irregular sampling rate challenge of existing neural network models for a continuous time series, i.e., length and dynamic nature, (iii)~how to reduce the training and evaluation time of existing Neural ODE systems? This work leverages the mathematical foundation of ODEs to redesign traditional RNNs such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU). The main contribution of this paper is to illustrate the design of two new ODE-based RNN models (GRU-ODE model and LSTM-ODE) which can compute the hidden state and cell state at any point of time using an ODE solver. These models reduce the computation overhead of hidden state and cell state by a vast amount. The performance evaluation of these two new models for learning continuous time series with irregular sampling rate is then demonstrated. Experiments show that these new ODE based RNN models require less training time than Latent ODEs and conventional Neural ODEs. They can achieve higher accuracy quickly, and the design of the neural network is simpler than, previous neural ODE systems.

Neural ODEs for Informative Missingness in Multivariate Time Series

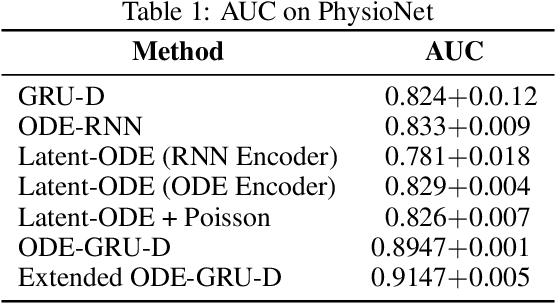
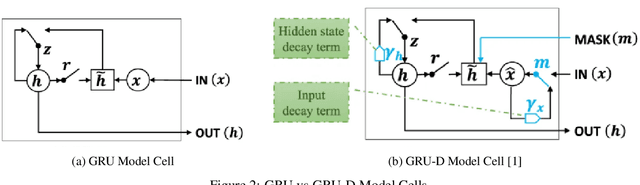
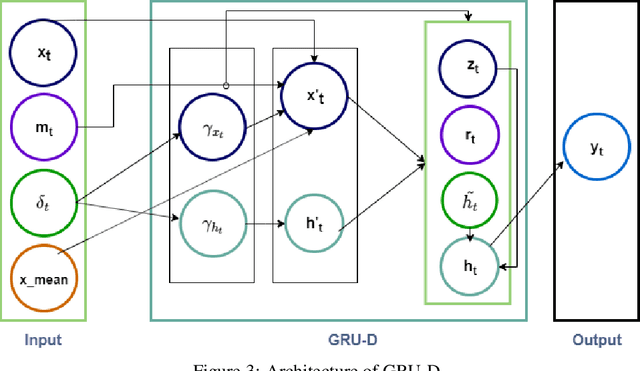
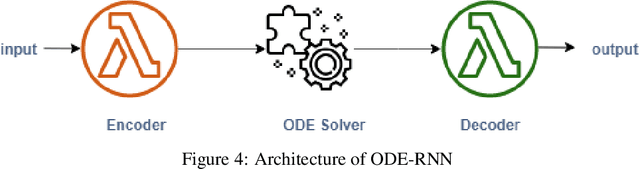
Informative missingness is unavoidable in the digital processing of continuous time series, where the value for one or more observations at different time points are missing. Such missing observations are one of the major limitations of time series processing using deep learning. Practical applications, e.g., sensor data, healthcare, weather, generates data that is in truth continuous in time, and informative missingness is a common phenomenon in these datasets. These datasets often consist of multiple variables, and often there are missing values for one or many of these variables. This characteristic makes time series prediction more challenging, and the impact of missing input observations on the accuracy of the final output can be significant. A recent novel deep learning model called GRU-D is one early attempt to address informative missingness in time series data. On the other hand, a new family of neural networks called Neural ODEs (Ordinary Differential Equations) are natural and efficient for processing time series data which is continuous in time. In this paper, a deep learning model is proposed that leverages the effective imputation of GRU-D, and the temporal continuity of Neural ODEs. A time series classification task performed on the PhysioNet dataset demonstrates the performance of this architecture.

Automatic differentiation in machine learning: a survey

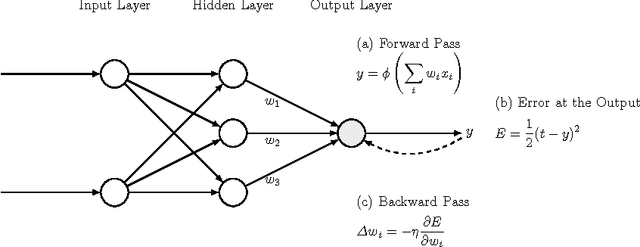
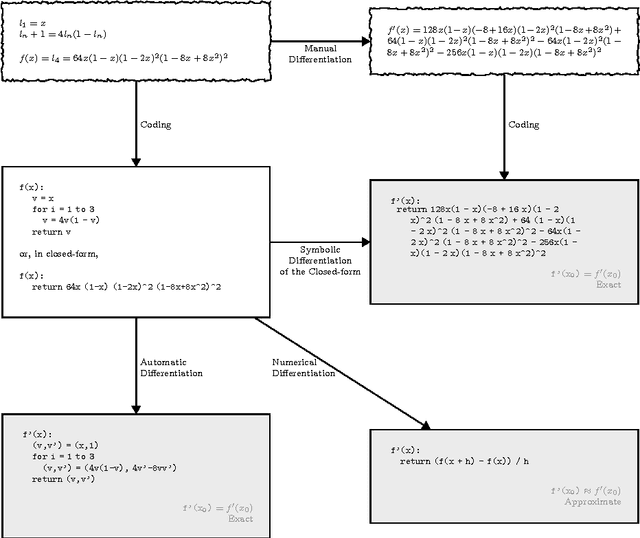
Derivatives, mostly in the form of gradients and Hessians, are ubiquitous in machine learning. Automatic differentiation (AD), also called algorithmic differentiation or simply "autodiff", is a family of techniques similar to but more general than backpropagation for efficiently and accurately evaluating derivatives of numeric functions expressed as computer programs. AD is a small but established field with applications in areas including computational fluid dynamics, atmospheric sciences, and engineering design optimization. Until very recently, the fields of machine learning and AD have largely been unaware of each other and, in some cases, have independently discovered each other's results. Despite its relevance, general-purpose AD has been missing from the machine learning toolbox, a situation slowly changing with its ongoing adoption under the names "dynamic computational graphs" and "differentiable programming". We survey the intersection of AD and machine learning, cover applications where AD has direct relevance, and address the main implementation techniques. By precisely defining the main differentiation techniques and their interrelationships, we aim to bring clarity to the usage of the terms "autodiff", "automatic differentiation", and "symbolic differentiation" as these are encountered more and more in machine learning settings.

Tricks from Deep Learning

The deep learning community has devised a diverse set of methods to make gradient optimization, using large datasets, of large and highly complex models with deeply cascaded nonlinearities, practical. Taken as a whole, these methods constitute a breakthrough, allowing computational structures which are quite wide, very deep, and with an enormous number and variety of free parameters to be effectively optimized. The result now dominates much of practical machine learning, with applications in machine translation, computer vision, and speech recognition. Many of these methods, viewed through the lens of algorithmic differentiation (AD), can be seen as either addressing issues with the gradient itself, or finding ways of achieving increased efficiency using tricks that are AD-related, but not provided by current AD systems. The goal of this paper is to explain not just those methods of most relevance to AD, but also the technical constraints and mindset which led to their discovery. After explaining this context, we present a "laundry list" of methods developed by the deep learning community. Two of these are discussed in further mathematical detail: a way to dramatically reduce the size of the tape when performing reverse-mode AD on a (theoretically) time-reversible process like an ODE integrator; and a new mathematical insight that allows for the implementation of a stochastic Newton's method.

DiffSharp: An AD Library for .NET Languages

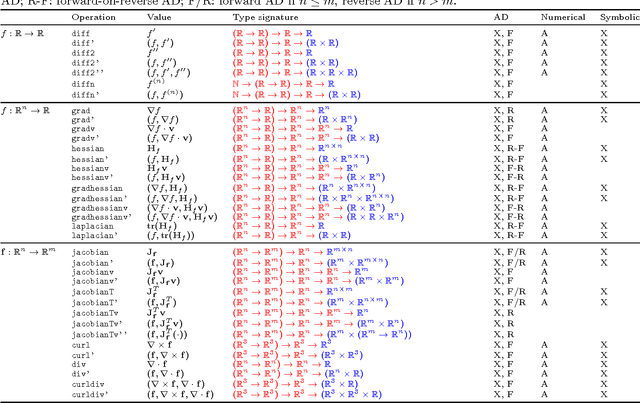
DiffSharp is an algorithmic differentiation or automatic differentiation (AD) library for the .NET ecosystem, which is targeted by the C# and F# languages, among others. The library has been designed with machine learning applications in mind, allowing very succinct implementations of models and optimization routines. DiffSharp is implemented in F# and exposes forward and reverse AD operators as general nestable higher-order functions, usable by any .NET language. It provides high-performance linear algebra primitives---scalars, vectors, and matrices, with a generalization to tensors underway---that are fully supported by all the AD operators, and which use a BLAS/LAPACK backend via the highly optimized OpenBLAS library. DiffSharp currently uses operator overloading, but we are developing a transformation-based version of the library using F#'s "code quotation" metaprogramming facility. Work on a CUDA-based GPU backend is also underway.

Binomial Checkpointing for Arbitrary Programs with No User Annotation

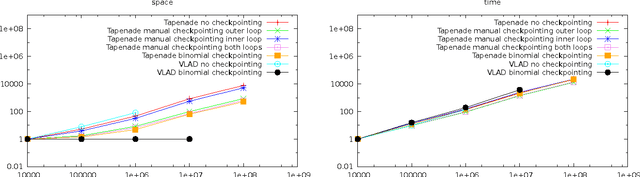
Heretofore, automatic checkpointing at procedure-call boundaries, to reduce the space complexity of reverse mode, has been provided by systems like Tapenade. However, binomial checkpointing, or treeverse, has only been provided in Automatic Differentiation (AD) systems in special cases, e.g., through user-provided pragmas on DO loops in Tapenade, or as the nested taping mechanism in adol-c for time integration processes, which requires that user code be refactored. We present a framework for applying binomial checkpointing to arbitrary code with no special annotation or refactoring required. This is accomplished by applying binomial checkpointing directly to a program trace. This trace is produced by a general-purpose checkpointing mechanism that is orthogonal to AD.

Automatic Differentiation of Algorithms for Machine Learning

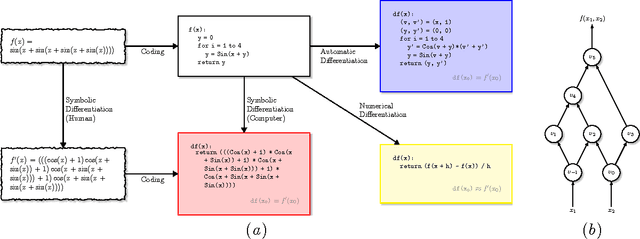
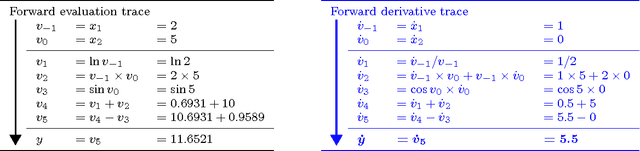
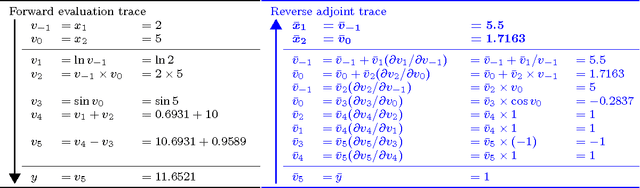
Automatic differentiation---the mechanical transformation of numeric computer programs to calculate derivatives efficiently and accurately---dates to the origin of the computer age. Reverse mode automatic differentiation both antedates and generalizes the method of backwards propagation of errors used in machine learning. Despite this, practitioners in a variety of fields, including machine learning, have been little influenced by automatic differentiation, and make scant use of available tools. Here we review the technique of automatic differentiation, describe its two main modes, and explain how it can benefit machine learning practitioners. To reach the widest possible audience our treatment assumes only elementary differential calculus, and does not assume any knowledge of linear algebra.

Block Coordinate Descent for Sparse NMF

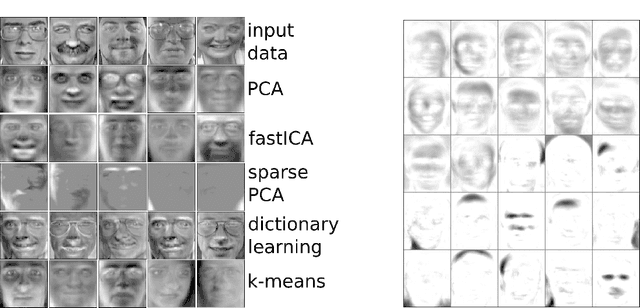
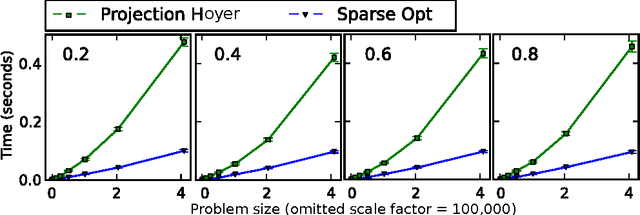
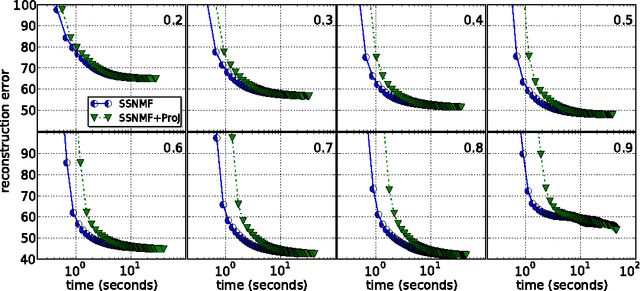
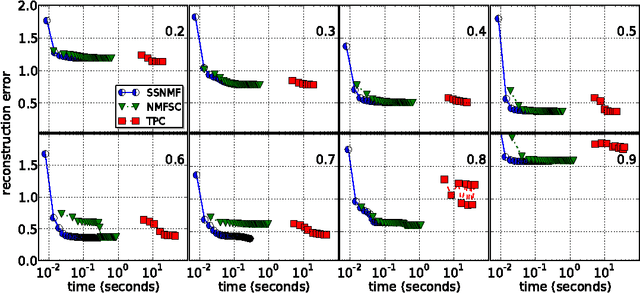
Nonnegative matrix factorization (NMF) has become a ubiquitous tool for data analysis. An important variant is the sparse NMF problem which arises when we explicitly require the learnt features to be sparse. A natural measure of sparsity is the L$_0$ norm, however its optimization is NP-hard. Mixed norms, such as L$_1$/L$_2$ measure, have been shown to model sparsity robustly, based on intuitive attributes that such measures need to satisfy. This is in contrast to computationally cheaper alternatives such as the plain L$_1$ norm. However, present algorithms designed for optimizing the mixed norm L$_1$/L$_2$ are slow and other formulations for sparse NMF have been proposed such as those based on L$_1$ and L$_0$ norms. Our proposed algorithm allows us to solve the mixed norm sparsity constraints while not sacrificing computation time. We present experimental evidence on real-world datasets that shows our new algorithm performs an order of magnitude faster compared to the current state-of-the-art solvers optimizing the mixed norm and is suitable for large-scale datasets.

Bounds on Query Convergence

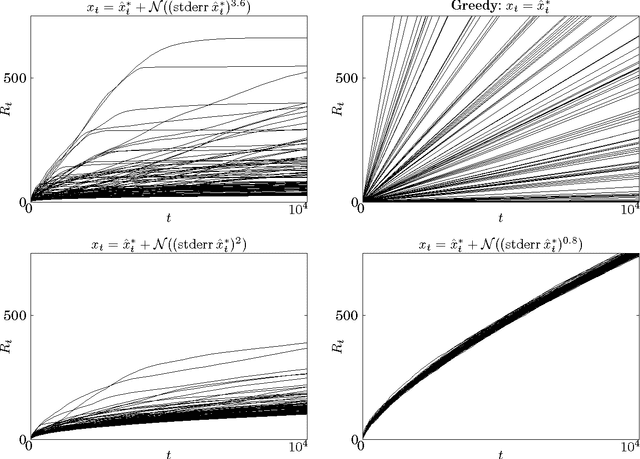
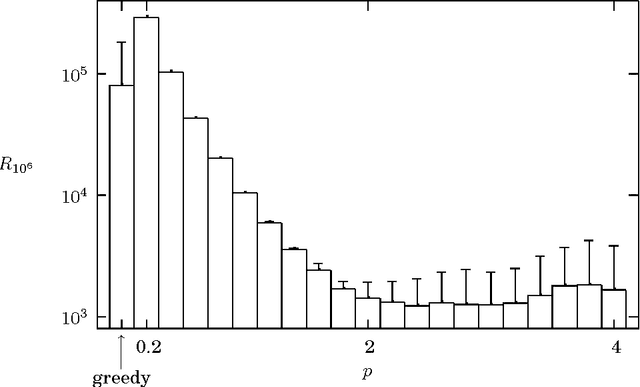
The problem of finding an optimum using noisy evaluations of a smooth cost function arises in many contexts, including economics, business, medicine, experiment design, and foraging theory. We derive an asymptotic bound E[ (x_t - x*)^2 ] >= O(1/sqrt(t)) on the rate of convergence of a sequence (x_0, x_1, >...) generated by an unbiased feedback process observing noisy evaluations of an unknown quadratic function maximised at x*. The bound is tight, as the proof leads to a simple algorithm which meets it. We further establish a bound on the total regret, E[ sum_{i=1..t} (x_i - x*)^2 ] >= O(sqrt(t)) These bounds may impose practical limitations on an agent's performance, as O(eps^-4) queries are made before the queries converge to x* with eps accuracy.