Recent Trends in Modelling the Continuous Time Series using Deep Learning: A Survey

Continuous-time series is essential for different modern application areas, e.g. healthcare, automobile, energy, finance, Internet of things (IoT) and other related areas. Different application needs to process as well as analyse a massive amount of data in time series structure in order to determine the data-driven result, for example, financial trend prediction, potential probability of the occurrence of a particular event occurrence identification, patient health record processing and so many more. However, modeling real-time data using a continuous-time series is challenging since the dynamical systems behind the data could be a differential equation. Several research works have tried to solve the challenges of modelling the continuous-time series using different neural network models and approaches for data processing and learning. The existing deep learning models are not free from challenges and limitations due to diversity among different attributes, behaviour, duration of steps, energy, and data sampling rate. This paper has described the general problem domain of time series and reviewed the challenges of modelling the continuous time series. We have presented a comparative analysis of recent developments in deep learning models and their contribution to solving different difficulties of modelling the continuous time series. We have also identified the limitations of the existing neural network model and open issues. The main goal of this review is to understand the recent trend of neural network models used in a different real-world application with continuous-time data.

Continuous Convolutional Neural Networks: Coupled Neural PDE and ODE

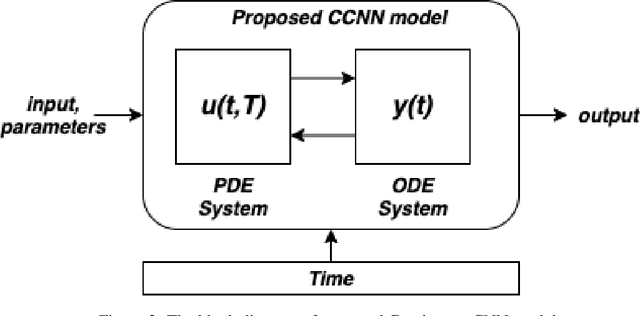
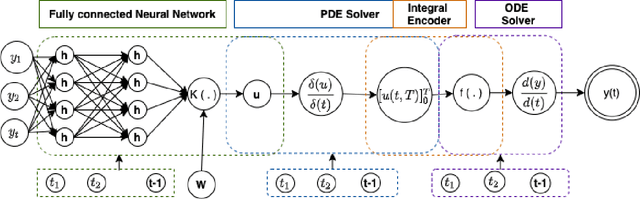
Recent work in deep learning focuses on solving physical systems in the Ordinary Differential Equation or Partial Differential Equation. This current work proposed a variant of Convolutional Neural Networks (CNNs) that can learn the hidden dynamics of a physical system using ordinary differential equation (ODEs) systems (ODEs) and Partial Differential Equation systems (PDEs). Instead of considering the physical system such as image, time -series as a system of multiple layers, this new technique can model a system in the form of Differential Equation (DEs). The proposed method has been assessed by solving several steady-state PDEs on irregular domains, including heat equations, Navier-Stokes equations.

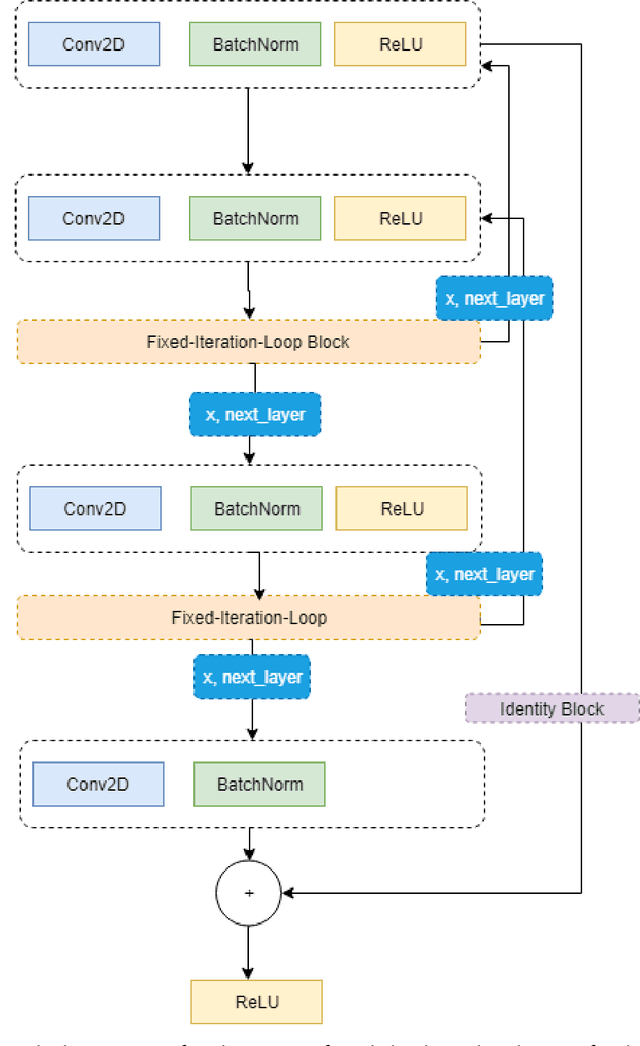
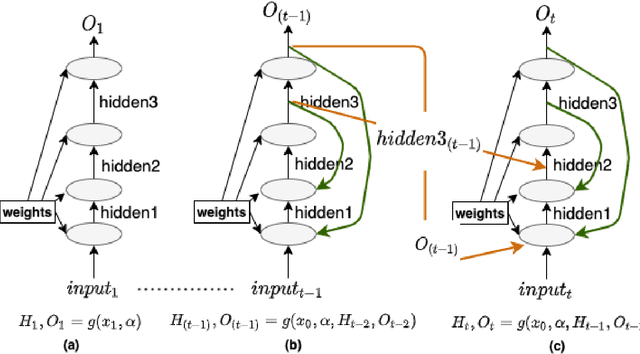
Neural Network based on Automatic Differentiation Transformation of Numeric Iterate-to-Fixedpoint

This work proposes a Neural Network model that can control its depth using an iterate-to-fixed-point operator. The architecture starts with a standard layered Network but with added connections from current later to earlier layers, along with a gate to make them inactive under most circumstances. These ``temporal wormhole'' connections create a shortcut that allows the Neural Network to use the information available at deeper layers and re-do earlier computations with modulated inputs. End-to-end training is accomplished by using appropriate calculations for a numeric iterate-to-fixed-point operator. In a typical case, where the ``wormhole'' connections are inactive, this is inexpensive; but when they are active, the network takes a longer time to settle down, and the gradient calculation is also more laborious, with an effect similar to making the network deeper. In contrast to the existing skip-connection concept, this proposed technique enables information to flow up and down in the network. Furthermore, the flow of information follows a fashion that seems analogous to the afferent and efferent flow of information through layers of processing in the brain. We evaluate models that use this novel mechanism on different long-term dependency tasks. The results are competitive with other studies, showing that the proposed model contributes significantly to overcoming traditional deep learning models' vanishing gradient descent problem. At the same time, the training time is significantly reduced, as the ``easy'' input cases are processed more quickly than ``difficult'' ones.

ECG synthesis with Neural ODE and GAN models

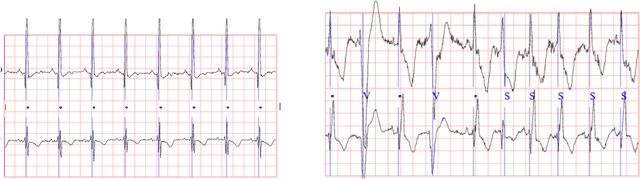
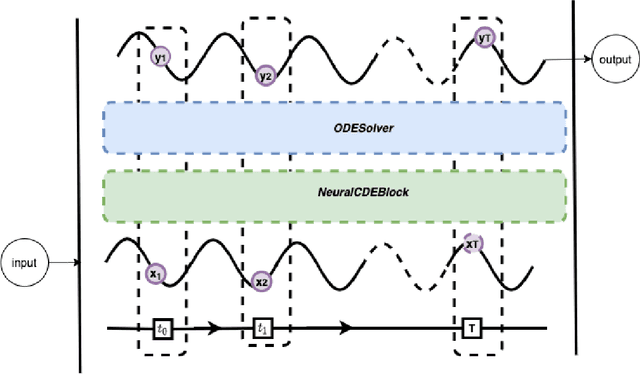
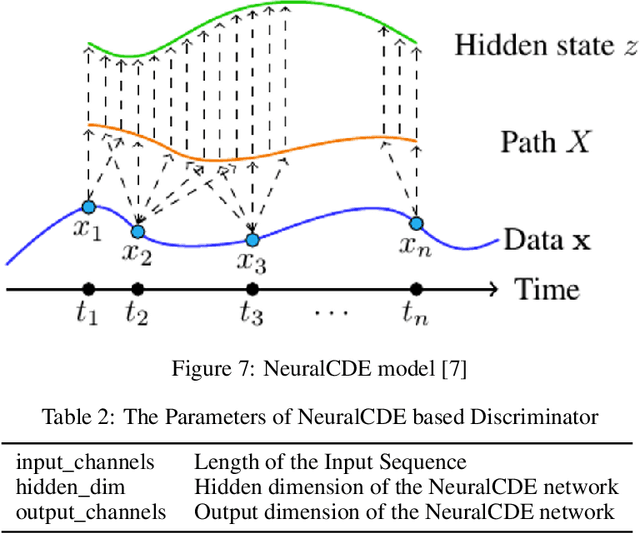
Continuous medical time series data such as ECG is one of the most complex time series due to its dynamic and high dimensional characteristics. In addition, due to its sensitive nature, privacy concerns and legal restrictions, it is often even complex to use actual data for different medical research. As a result, generating continuous medical time series is a very critical research area. Several research works already showed that the ability of generative adversarial networks (GANs) in the case of continuous medical time series generation is promising. Most medical data generation works, such as ECG synthesis, are mainly driven by the GAN model and its variation. On the other hand, Some recent work on Neural Ordinary Differential Equation (Neural ODE) demonstrates its strength against informative missingness, high dimension as well as dynamic nature of continuous time series. Instead of considering continuous-time series as a discrete-time sequence, Neural ODE can train continuous time series in real-time continuously. In this work, we used Neural ODE based model to generate synthetic sine waves and synthetic ECG. We introduced a new technique to design the generative adversarial network with Neural ODE based Generator and Discriminator. We developed three new models to synthesise continuous medical data. Different evaluation metrics are then used to quantitatively assess the quality of generated synthetic data for real-world applications and data analysis. Another goal of this work is to combine the strength of GAN and Neural ODE to generate synthetic continuous medical time series data such as ECG. We also evaluated both the GAN model and the Neural ODE model to understand the comparative efficiency of models from the GAN and Neural ODE family in medical data synthesis.

HeunNet: Extending ResNet using Heun's Methods

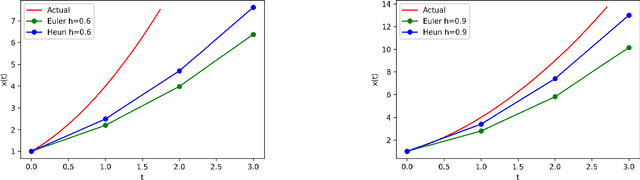
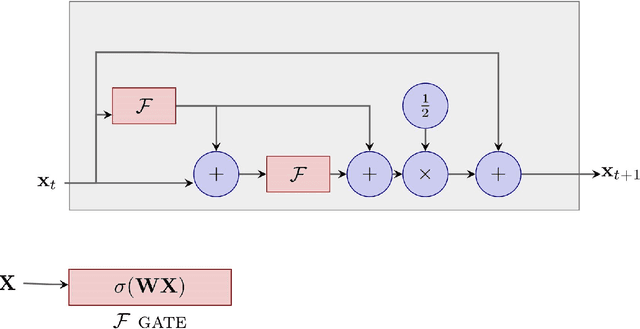
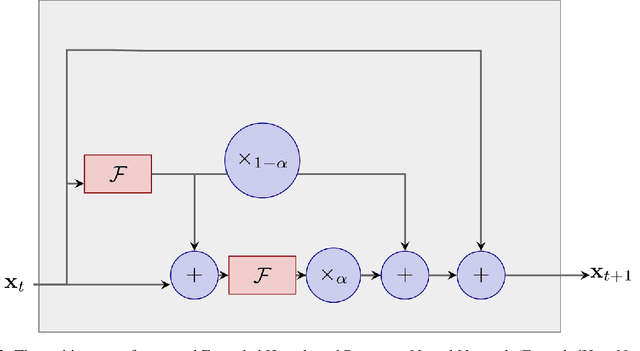
There is an analogy between the ResNet (Residual Network) architecture for deep neural networks and an Euler solver for an ODE. The transformation performed by each layer resembles an Euler step in solving an ODE. We consider the Heun Method, which involves a single predictor-corrector cycle, and complete the analogy, building a predictor-corrector variant of ResNet, which we call a HeunNet. Just as Heun's method is more accurate than Euler's, experiments show that HeunNet achieves high accuracy with low computational (both training and test) time compared to both vanilla recurrent neural networks and other ResNet variants.

Neural Ordinary Differential Equation based Recurrent Neural Network Model

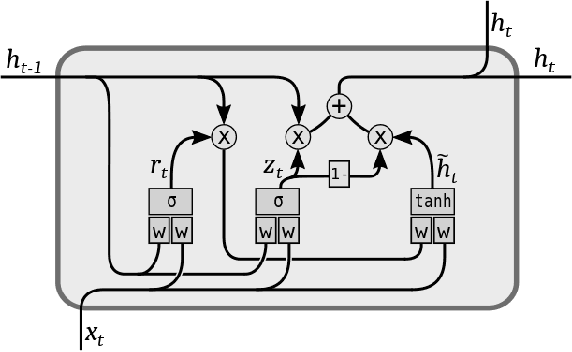
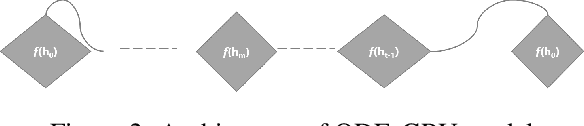
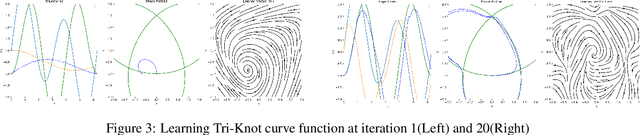
Neural differential equations are a promising new member in the neural network family. They show the potential of differential equations for time series data analysis. In this paper, the strength of the ordinary differential equation (ODE) is explored with a new extension. The main goal of this work is to answer the following questions: (i)~can ODE be used to redefine the existing neural network model? (ii)~can Neural ODEs solve the irregular sampling rate challenge of existing neural network models for a continuous time series, i.e., length and dynamic nature, (iii)~how to reduce the training and evaluation time of existing Neural ODE systems? This work leverages the mathematical foundation of ODEs to redesign traditional RNNs such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU). The main contribution of this paper is to illustrate the design of two new ODE-based RNN models (GRU-ODE model and LSTM-ODE) which can compute the hidden state and cell state at any point of time using an ODE solver. These models reduce the computation overhead of hidden state and cell state by a vast amount. The performance evaluation of these two new models for learning continuous time series with irregular sampling rate is then demonstrated. Experiments show that these new ODE based RNN models require less training time than Latent ODEs and conventional Neural ODEs. They can achieve higher accuracy quickly, and the design of the neural network is simpler than, previous neural ODE systems.

Neural ODEs for Informative Missingness in Multivariate Time Series

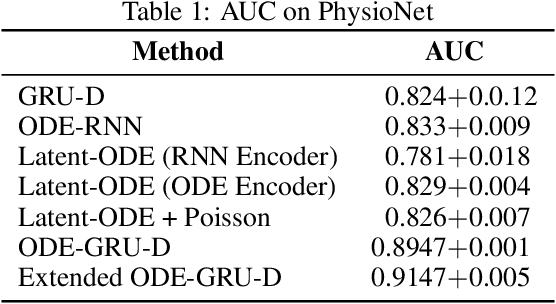
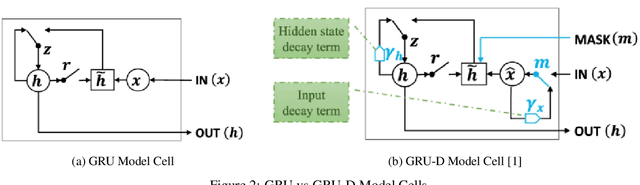
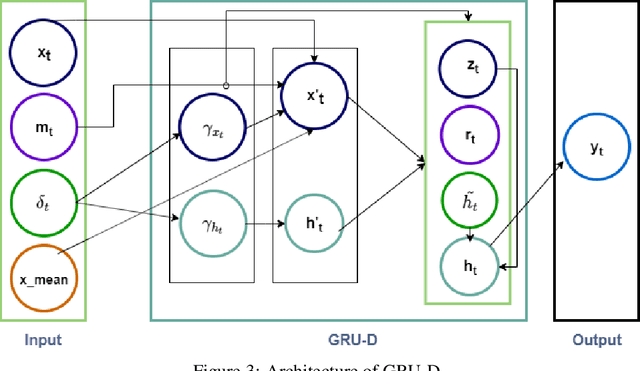
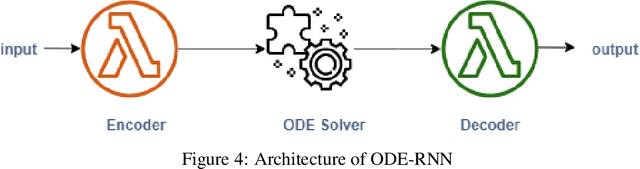
Informative missingness is unavoidable in the digital processing of continuous time series, where the value for one or more observations at different time points are missing. Such missing observations are one of the major limitations of time series processing using deep learning. Practical applications, e.g., sensor data, healthcare, weather, generates data that is in truth continuous in time, and informative missingness is a common phenomenon in these datasets. These datasets often consist of multiple variables, and often there are missing values for one or many of these variables. This characteristic makes time series prediction more challenging, and the impact of missing input observations on the accuracy of the final output can be significant. A recent novel deep learning model called GRU-D is one early attempt to address informative missingness in time series data. On the other hand, a new family of neural networks called Neural ODEs (Ordinary Differential Equations) are natural and efficient for processing time series data which is continuous in time. In this paper, a deep learning model is proposed that leverages the effective imputation of GRU-D, and the temporal continuity of Neural ODEs. A time series classification task performed on the PhysioNet dataset demonstrates the performance of this architecture.