Action-List Reinforcement Learning Syndrome Decoding for Binary Linear Block Codes

This paper explores the application of reinforcement learning techniques to enhance the performance of decoding of linear block codes based on flipping bits and finding optimal decisions. We describe the methodology for mapping the iterative decoding process into Markov Decision Processes (MDPs) and propose different methods to reduce the number of states in the MDP. A truncated MDP is proposed to reduce the number of states in the MDP by learning a Hamming ball with a specified radius around codewords. We then propose a general scheme for reinforcement learning based decoders applicable to any class of codes to improve the performance of decoders. We call this scheme an action-list decoding. We design an action-list decoder based on the Deep-Q network values that substantially enhance performance. We also get benefit of automorphism group of code to further improve the code performance. Additionally, we propose a feedback-based method to exploit and enhance the performance of existing high-performing decoders by applying reinforcement learning algorithms after the existing decoders. These approaches effectively reduces the complexity of the reinforcement learning block. Finally, we present experimental results for the Low-Density Parity Check (LDPC) codes over the Binary Symmetric Channel (BSC) to demonstrate the efficiency of the proposed methods.

Generalization Bounds for Neural Belief Propagation Decoders

Machine learning based approaches are being increasingly used for designing decoders for next generation communication systems. One widely used framework is neural belief propagation (NBP), which unfolds the belief propagation (BP) iterations into a deep neural network and the parameters are trained in a data-driven manner. NBP decoders have been shown to improve upon classical decoding algorithms. In this paper, we investigate the generalization capabilities of NBP decoders. Specifically, the generalization gap of a decoder is the difference between empirical and expected bit-error-rate(s). We present new theoretical results which bound this gap and show the dependence on the decoder complexity, in terms of code parameters (blocklength, message length, variable/check node degrees), decoding iterations, and the training dataset size. Results are presented for both regular and irregular parity-check matrices. To the best of our knowledge, this is the first set of theoretical results on generalization performance of neural network based decoders. We present experimental results to show the dependence of generalization gap on the training dataset size, and decoding iterations for different codes.

FAID Diversity via Neural Networks

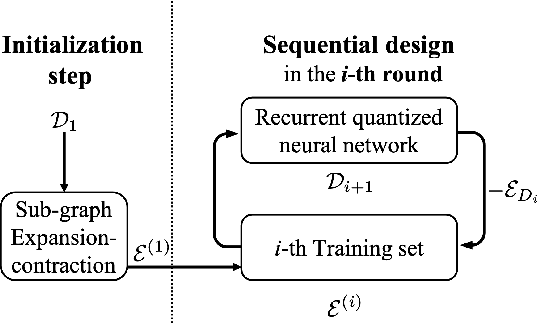
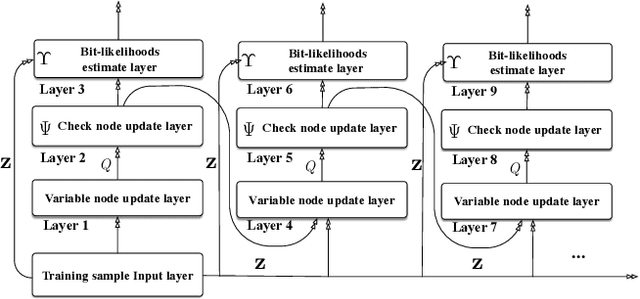
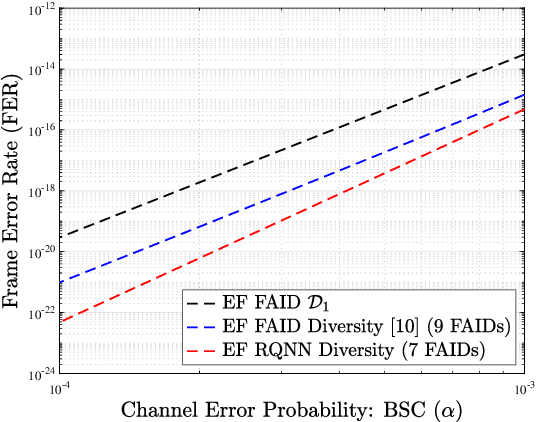
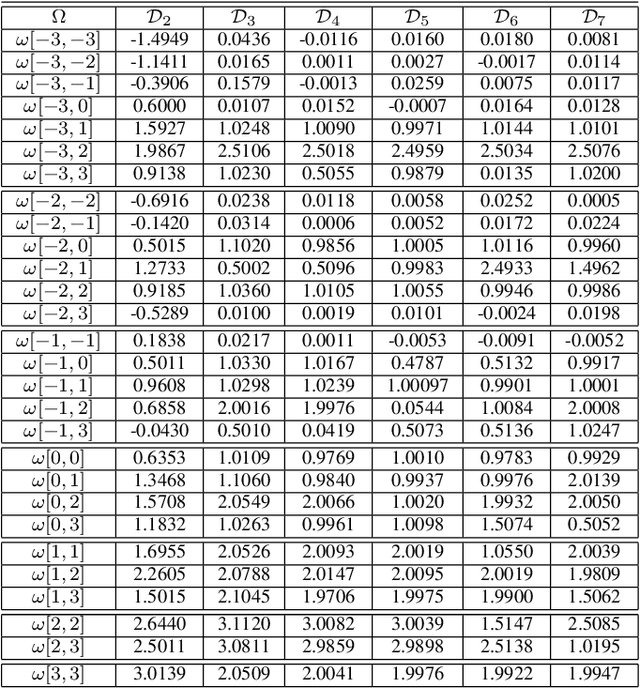
Decoder diversity is a powerful error correction framework in which a collection of decoders collaboratively correct a set of error patterns otherwise uncorrectable by any individual decoder. In this paper, we propose a new approach to design the decoder diversity of finite alphabet iterative decoders (FAIDs) for Low-Density Parity Check (LDPC) codes over the binary symmetric channel (BSC), for the purpose of lowering the error floor while guaranteeing the waterfall performance. The proposed decoder diversity is achieved by training a recurrent quantized neural network (RQNN) to learn/design FAIDs. We demonstrated for the first time that a machine-learned decoder can surpass in performance a man-made decoder of the same complexity. As RQNNs can model a broad class of FAIDs, they are capable of learning an arbitrary FAID. To provide sufficient knowledge of the error floor to the RQNN, the training sets are constructed by sampling from the set of most problematic error patterns - trapping sets. In contrast to the existing methods that use the cross-entropy function as the loss function, we introduce a frame-error-rate (FER) based loss function to train the RQNN with the objective of correcting specific error patterns rather than reducing the bit error rate (BER). The examples and simulation results show that the RQNN-aided decoder diversity increases the error correction capability of LDPC codes and lowers the error floor.