On User-Level Private Convex Optimization

We introduce a new mechanism for stochastic convex optimization (SCO) with user-level differential privacy guarantees. The convergence rates of this mechanism are similar to those in the prior work of Levy et al. (2021); Narayanan et al. (2022), but with two important improvements. Our mechanism does not require any smoothness assumptions on the loss. Furthermore, our bounds are also the first where the minimum number of users needed for user-level privacy has no dependence on the dimension and only a logarithmic dependence on the desired excess error. The main idea underlying the new mechanism is to show that the optimizers of strongly convex losses have low local deletion sensitivity, along with an output perturbation method for functions with low local deletion sensitivity, which could be of independent interest.

Regression with Label Differential Privacy

We study the task of training regression models with the guarantee of label differential privacy (DP). Based on a global prior distribution on label values, which could be obtained privately, we derive a label DP randomization mechanism that is optimal under a given regression loss function. We prove that the optimal mechanism takes the form of a ``randomized response on bins'', and propose an efficient algorithm for finding the optimal bin values. We carry out a thorough experimental evaluation on several datasets demonstrating the efficacy of our algorithm.

Private Ad Modeling with DP-SGD

A well-known algorithm in privacy-preserving ML is differentially private stochastic gradient descent (DP-SGD). While this algorithm has been evaluated on text and image data, it has not been previously applied to ads data, which are notorious for their high class imbalance and sparse gradient updates. In this work we apply DP-SGD to several ad modeling tasks including predicting click-through rates, conversion rates, and number of conversion events, and evaluate their privacy-utility trade-off on real-world datasets. Our work is the first to empirically demonstrate that DP-SGD can provide both privacy and utility for ad modeling tasks.

Private Isotonic Regression

In this paper, we consider the problem of differentially private (DP) algorithms for isotonic regression. For the most general problem of isotonic regression over a partially ordered set (poset) $\mathcal{X}$ and for any Lipschitz loss function, we obtain a pure-DP algorithm that, given $n$ input points, has an expected excess empirical risk of roughly $\mathrm{width}(\mathcal{X}) \cdot \log|\mathcal{X}| / n$, where $\mathrm{width}(\mathcal{X})$ is the width of the poset. In contrast, we also obtain a near-matching lower bound of roughly $(\mathrm{width}(\mathcal{X}) + \log |\mathcal{X}|) / n$, that holds even for approximate-DP algorithms. Moreover, we show that the above bounds are essentially the best that can be obtained without utilizing any further structure of the poset. In the special case of a totally ordered set and for $\ell_1$ and $\ell_2^2$ losses, our algorithm can be implemented in near-linear running time; we also provide extensions of this algorithm to the problem of private isotonic regression with additional structural constraints on the output function.

Anonymized Histograms in Intermediate Privacy Models

We study the problem of privately computing the anonymized histogram (a.k.a. unattributed histogram), which is defined as the histogram without item labels. Previous works have provided algorithms with $\ell_1$- and $\ell_2^2$-errors of $O_\varepsilon(\sqrt{n})$ in the central model of differential privacy (DP). In this work, we provide an algorithm with a nearly matching error guarantee of $\tilde{O}_\varepsilon(\sqrt{n})$ in the shuffle DP and pan-private models. Our algorithm is very simple: it just post-processes the discrete Laplace-noised histogram! Using this algorithm as a subroutine, we show applications in privately estimating symmetric properties of distributions such as entropy, support coverage, and support size.

Algorithms with More Granular Differential Privacy Guarantees

Differential privacy is often applied with a privacy parameter that is larger than the theory suggests is ideal; various informal justifications for tolerating large privacy parameters have been proposed. In this work, we consider partial differential privacy (DP), which allows quantifying the privacy guarantee on a per-attribute basis. In this framework, we study several basic data analysis and learning tasks, and design algorithms whose per-attribute privacy parameter is smaller that the best possible privacy parameter for the entire record of a person (i.e., all the attributes).

Faster Privacy Accounting via Evolving Discretization

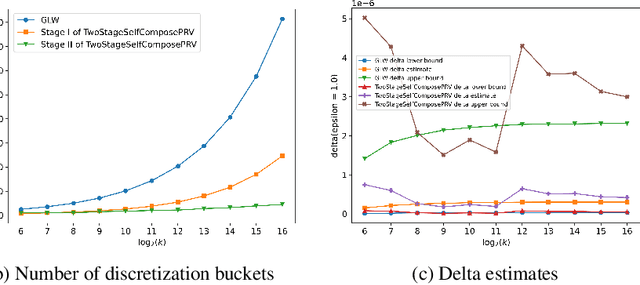
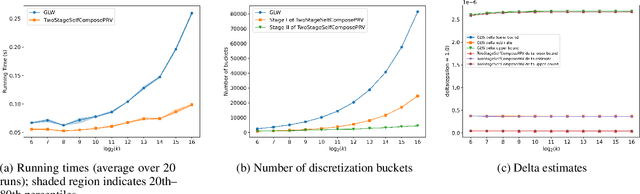
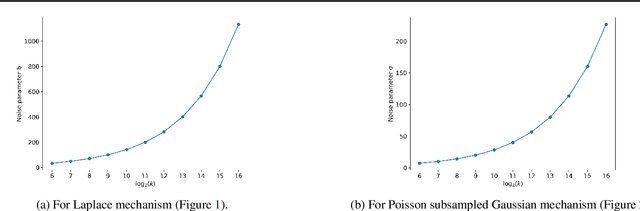
We introduce a new algorithm for numerical composition of privacy random variables, useful for computing the accurate differential privacy parameters for composition of mechanisms. Our algorithm achieves a running time and memory usage of $\mathrm{polylog}(k)$ for the task of self-composing a mechanism, from a broad class of mechanisms, $k$ times; this class, e.g., includes the sub-sampled Gaussian mechanism, that appears in the analysis of differentially private stochastic gradient descent. By comparison, recent work by Gopi et al. (NeurIPS 2021) has obtained a running time of $\widetilde{O}(\sqrt{k})$ for the same task. Our approach extends to the case of composing $k$ different mechanisms in the same class, improving upon their running time and memory usage from $\widetilde{O}(k^{1.5})$ to $\widetilde{O}(k)$.

Connect the Dots: Tighter Discrete Approximations of Privacy Loss Distributions

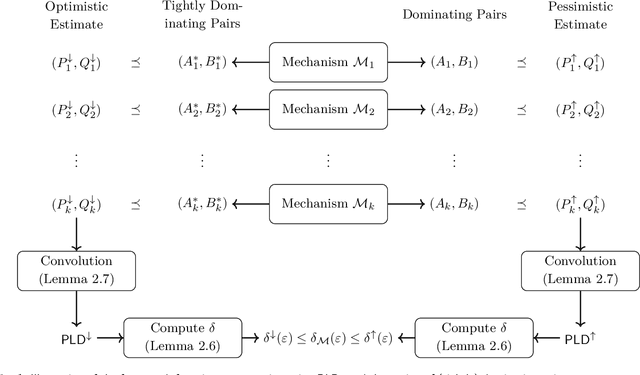
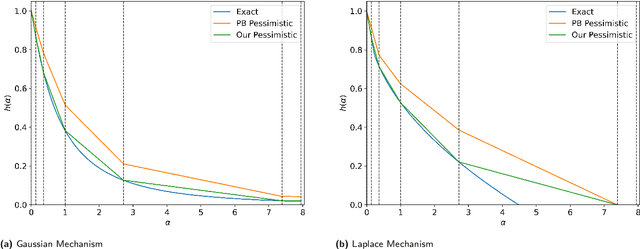
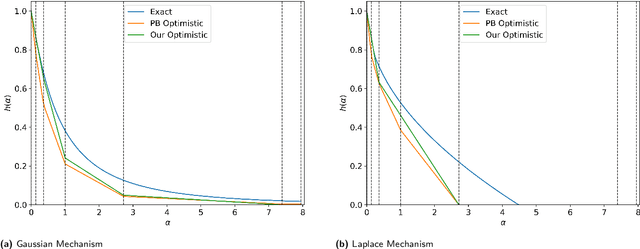
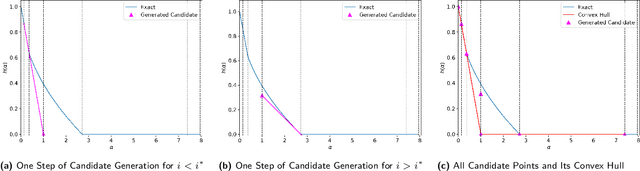
The privacy loss distribution (PLD) provides a tight characterization of the privacy loss of a mechanism in the context of differential privacy (DP). Recent work has shown that PLD-based accounting allows for tighter $(\varepsilon, \delta)$-DP guarantees for many popular mechanisms compared to other known methods. A key question in PLD-based accounting is how to approximate any (potentially continuous) PLD with a PLD over any specified discrete support. We present a novel approach to this problem. Our approach supports both pessimistic estimation, which overestimates the hockey-stick divergence (i.e., $\delta$) for any value of $\varepsilon$, and optimistic estimation, which underestimates the hockey-stick divergence. Moreover, we show that our pessimistic estimate is the best possible among all pessimistic estimates. Experimental evaluation shows that our approach can work with much larger discretization intervals while keeping a similar error bound compared to previous approaches and yet give a better approximation than existing methods.

User-Level Private Learning via Correlated Sampling

Most works in learning with differential privacy (DP) have focused on the setting where each user has a single sample. In this work, we consider the setting where each user holds $m$ samples and the privacy protection is enforced at the level of each user's data. We show that, in this setting, we may learn with a much fewer number of users. Specifically, we show that, as long as each user receives sufficiently many samples, we can learn any privately learnable class via an $(\epsilon, \delta)$-DP algorithm using only $O(\log(1/\delta)/\epsilon)$ users. For $\epsilon$-DP algorithms, we show that we can learn using only $O_{\epsilon}(d)$ users even in the local model, where $d$ is the probabilistic representation dimension. In both cases, we show a nearly-matching lower bound on the number of users required. A crucial component of our results is a generalization of global stability [Bun et al., FOCS 2020] that allows the use of public randomness. Under this relaxed notion, we employ a correlated sampling strategy to show that the global stability can be boosted to be arbitrarily close to one, at a polynomial expense in the number of samples.

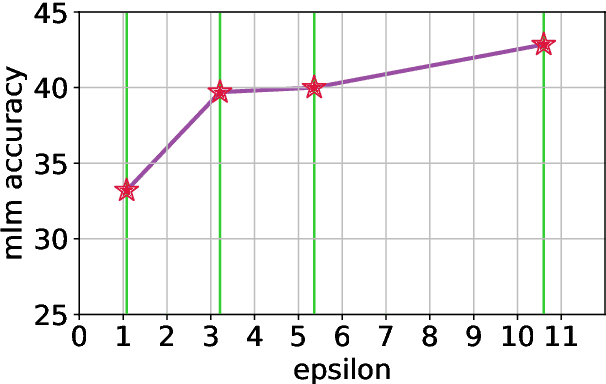
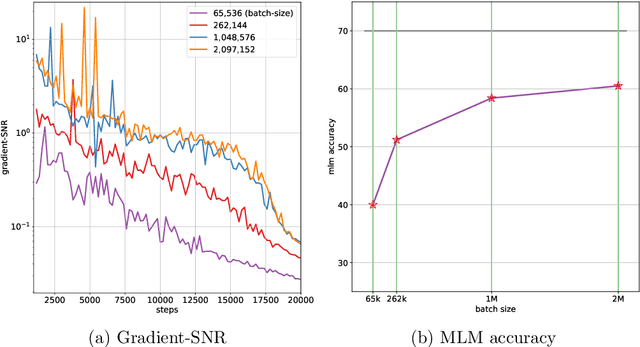
Large-Scale Differentially Private BERT

In this work, we study the large-scale pretraining of BERT-Large with differentially private SGD (DP-SGD). We show that combined with a careful implementation, scaling up the batch size to millions (i.e., mega-batches) improves the utility of the DP-SGD step for BERT; we also enhance its efficiency by using an increasing batch size schedule. Our implementation builds on the recent work of [SVK20], who demonstrated that the overhead of a DP-SGD step is minimized with effective use of JAX [BFH+18, FJL18] primitives in conjunction with the XLA compiler [XLA17]. Our implementation achieves a masked language model accuracy of 60.5% at a batch size of 2M, for $\epsilon = 5.36$. To put this number in perspective, non-private BERT models achieve an accuracy of $\sim$70%.