A General Framework for Dynamic MAPF using Multi-Shot ASP and Tunnels

MAPF problem aims to find plans for multiple agents in an environment within a given time, such that the agents do not collide with each other or obstacles. Motivated by the execution and monitoring of these plans, we study Dynamic MAPF (D-MAPF) problem, which allows changes such as agents entering/leaving the environment or obstacles being removed/moved. Considering the requirements of real-world applications in warehouses with the presence of humans, we introduce 1) a general definition for D-MAPF (applicable to variations of D-MAPF), 2) a new framework to solve D-MAPF (utilizing multi-shot computation, and allowing different methods to solve D-MAPF), and 3) a new ASP-based method to solve D-MAPF (combining advantages of replanning and repairing methods, with a novel concept of tunnels to specify where agents can move). We have illustrated the strengths and weaknesses of this method by experimental evaluations, from the perspectives of computational performance and quality of solutions.

Flexible and Explainable Solutions for Multi-Agent Path Finding Problems

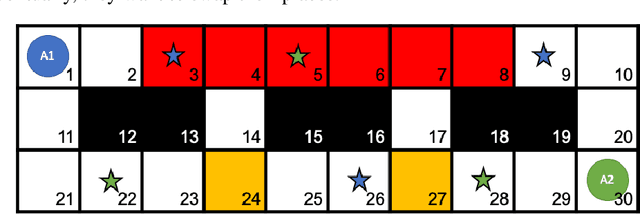
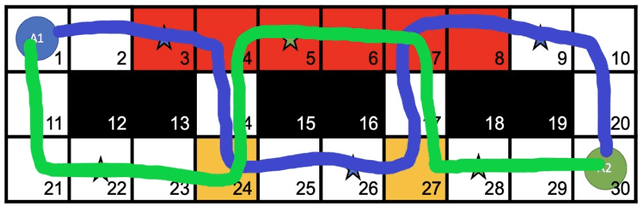
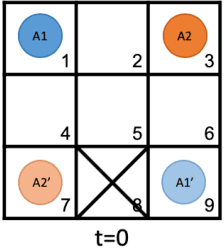
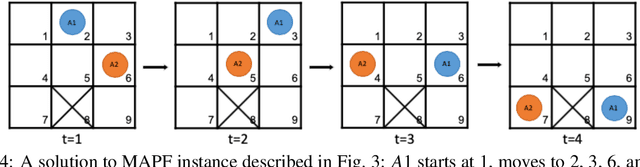
The multi-agent path finding (MAPF) problem is a combinatorial search problem that aims at finding paths for multiple agents (e.g., robots) in an environment (e.g., an autonomous warehouse) such that no two agents collide with each other, and subject to some constraints on the lengths of paths. The real-world applications of MAPF require flexibility (e.g., solving variations of MAPF) as well as explainability. In this study, both of these challenges are addressed and some flexible and explainable solutions for MAPF and its variants are introduced.

Explanation Generation for Multi-Modal Multi-Agent Path Finding with Optimal Resource Utilization using Answer Set Programming

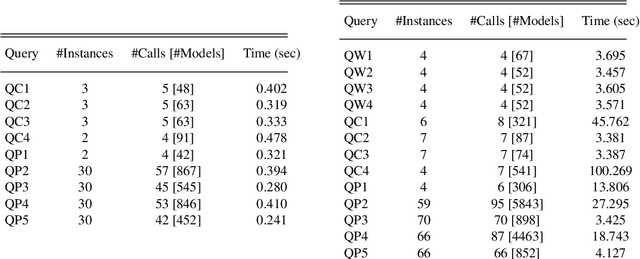
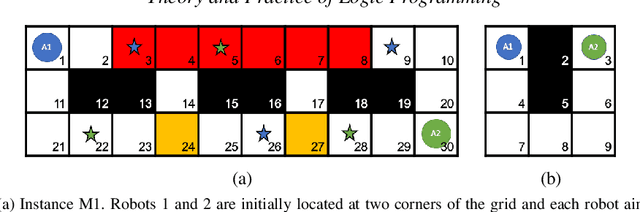
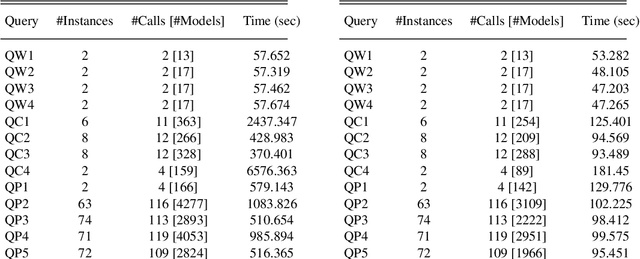
The multi-agent path finding (MAPF) problem is a combinatorial search problem that aims at finding paths for multiple agents (e.g., robots) in an environment (e.g., an autonomous warehouse) such that no two agents collide with each other, and subject to some constraints on the lengths of paths. We consider a general version of MAPF, called mMAPF, that involves multi-modal transportation modes (e.g., due to velocity constraints) and consumption of different types of resources (e.g., batteries). The real-world applications of mMAPF require flexibility (e.g., solving variations of mMAPF) as well as explainability. Our earlier studies on mMAPF have focused on the former challenge of flexibility. In this study, we focus on the latter challenge of explainability, and introduce a method for generating explanations for queries regarding the feasibility and optimality of solutions, the nonexistence of solutions, and the observations about solutions. Our method is based on answer set programming. This paper is under consideration for acceptance in TPLP.