Theoretical Guarantees for LT-TTD: A Unified Transformer-based Architecture for Two-Level Ranking Systems

Modern recommendation and search systems typically employ multi-stage ranking architectures to efficiently handle billions of candidates. The conventional approach uses distinct L1 (candidate retrieval) and L2 (re-ranking) models with different optimization objectives, introducing critical limitations including irreversible error propagation and suboptimal ranking. This paper identifies and analyzes the fundamental limitations of this decoupled paradigm and proposes LT-TTD (Listwise Transformer with Two-Tower Distillation), a novel unified architecture that bridges retrieval and ranking phases. Our approach combines the computational efficiency of two-tower models with the expressivity of transformers in a unified listwise learning framework. We provide a comprehensive theoretical analysis of our architecture and establish formal guarantees regarding error propagation mitigation, ranking quality improvements, and optimization convergence. We derive theoretical bounds showing that LT-TTD reduces the upper limit on irretrievable relevant items by a factor that depends on the knowledge distillation strength, and prove that our multi-objective optimization framework achieves a provably better global optimum than disjoint training. Additionally, we analyze the computational complexity of our approach, demonstrating that the asymptotic complexity remains within practical bounds for real-world applications. We also introduce UPQE, a novel evaluation metric specifically designed for unified ranking architectures that holistically captures retrieval quality, ranking performance, and computational efficiency.

TV-SurvCaus: Dynamic Representation Balancing for Causal Survival Analysis

Estimating the causal effect of time-varying treatments on survival outcomes is a challenging task in many domains, particularly in medicine where treatment protocols adapt over time. While recent advances in representation learning have improved causal inference for static treatments, extending these methods to dynamic treatment regimes with survival outcomes remains under-explored. In this paper, we introduce TV-SurvCaus, a novel framework that extends representation balancing techniques to the time-varying treatment setting for survival analysis. We provide theoretical guarantees through (1) a generalized bound for time-varying precision in estimation of heterogeneous effects, (2) variance control via sequential balancing weights, (3) consistency results for dynamic treatment regimes, (4) convergence rates for representation learning with temporal dependencies, and (5) a formal bound on the bias due to treatment-confounder feedback. Our neural architecture incorporates sequence modeling to handle temporal dependencies while balancing time-dependent representations. Through extensive experiments on both synthetic and real-world datasets, we demonstrate that TV-SurvCaus outperforms existing methods in estimating individualized treatment effects with time-varying covariates and treatments. Our framework advances the field of causal inference by enabling more accurate estimation of treatment effects in dynamic, longitudinal settings with survival outcomes.

SurvCaus : Representation Balancing for Survival Causal Inference

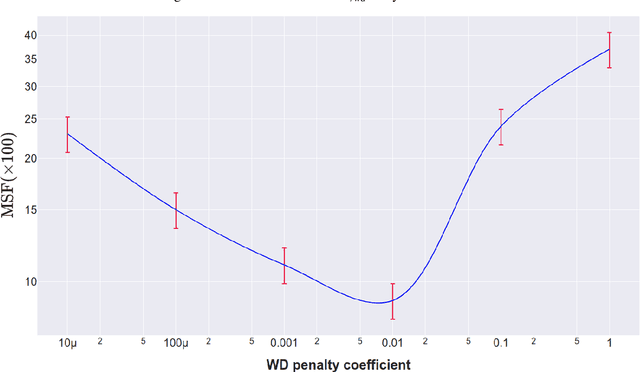
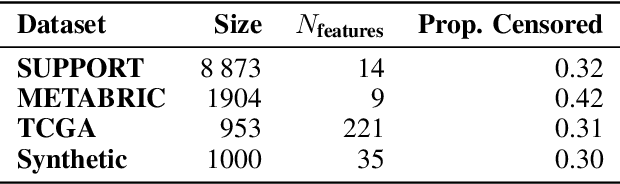
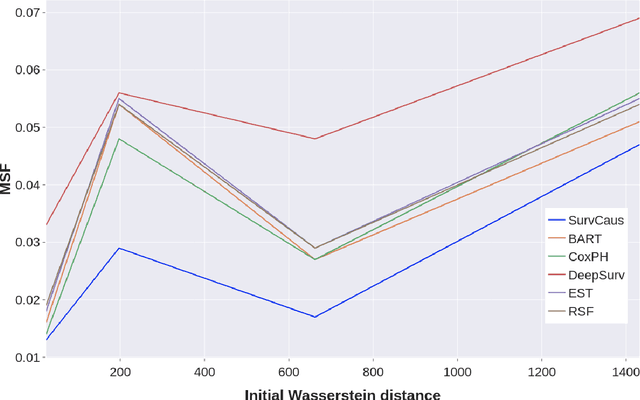
Individual Treatment Effects (ITE) estimation methods have risen in popularity in the last years. Most of the time, individual effects are better presented as Conditional Average Treatment Effects (CATE). Recently, representation balancing techniques have gained considerable momentum in causal inference from observational data, still limited to continuous (and binary) outcomes. However, in numerous pathologies, the outcome of interest is a (possibly censored) survival time. Our paper proposes theoretical guarantees for a representation balancing framework applied to counterfactual inference in a survival setting using a neural network capable of predicting the factual and counterfactual survival functions (and then the CATE), in the presence of censorship, at the individual level. We also present extensive experiments on synthetic and semisynthetic datasets that show that the proposed extensions outperform baseline methods.