Asymptotic breakdown point analysis of the minimum density power divergence estimator under independent non-homogeneous setups

The minimum density power divergence estimator (MDPDE) has gained significant attention in the literature of robust inference due to its strong robustness properties and high asymptotic efficiency; it is relatively easy to compute and can be interpreted as a generalization of the classical maximum likelihood estimator. It has been successfully applied in various setups, including the case of independent and non-homogeneous (INH) observations that cover both classification and regression-type problems with a fixed design. While the local robustness of this estimator has been theoretically validated through the bounded influence function, no general result is known about the global reliability or the breakdown behavior of this estimator under the INH setup, except for the specific case of location-type models. In this paper, we extend the notion of asymptotic breakdown point from the case of independent and identically distributed data to the INH setup and derive a theoretical lower bound for the asymptotic breakdown point of the MDPDE, under some easily verifiable assumptions. These results are further illustrated with applications to some fixed design regression models and corroborated through extensive simulation studies.

Robust Principal Component Analysis using Density Power Divergence

Principal component analysis (PCA) is a widely employed statistical tool used primarily for dimensionality reduction. However, it is known to be adversely affected by the presence of outlying observations in the sample, which is quite common. Robust PCA methods using M-estimators have theoretical benefits, but their robustness drop substantially for high dimensional data. On the other end of the spectrum, robust PCA algorithms solving principal component pursuit or similar optimization problems have high breakdown, but lack theoretical richness and demand high computational power compared to the M-estimators. We introduce a novel robust PCA estimator based on the minimum density power divergence estimator. This combines the theoretical strength of the M-estimators and the minimum divergence estimators with a high breakdown guarantee regardless of data dimension. We present a computationally efficient algorithm for this estimate. Our theoretical findings are supported by extensive simulations and comparisons with existing robust PCA methods. We also showcase the proposed algorithm's applicability on two benchmark datasets and a credit card transactions dataset for fraud detection.

A New Robust Scalable Singular Value Decomposition Algorithm for Video Surveillance Background Modelling

A basic algorithmic task in automated video surveillance is to separate background and foreground objects. Camera tampering, noisy videos, low frame rate, etc., pose difficulties in solving the problem. A general approach which classifies the tampered frames, and performs subsequent analysis on the remaining frames after discarding the tampered ones, results in loss of information. We propose a robust singular value decomposition (SVD) approach based on the density power divergence to perform background separation robustly even in the presence of tampered frames. We also provide theoretical results and perform simulations to validate the superiority of the proposed method over the few existing robust SVD methods. Finally, we indicate several other use-cases of the proposed method to show its general applicability to a large range of problems.

A Novel Minimum Divergence Approach to Robust Speaker Identification

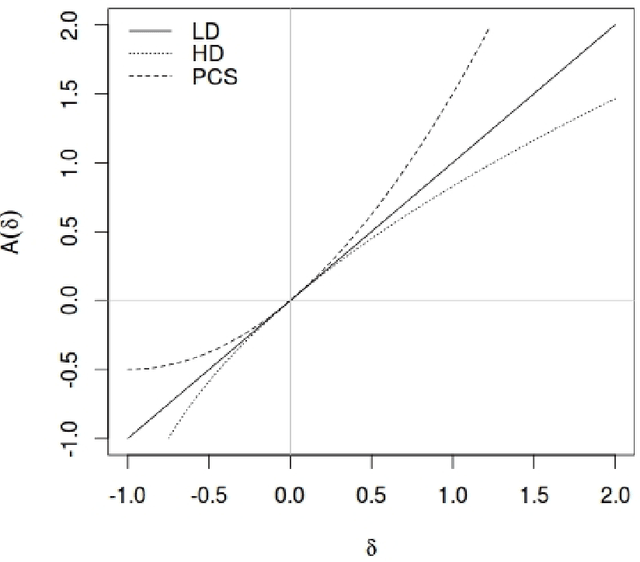
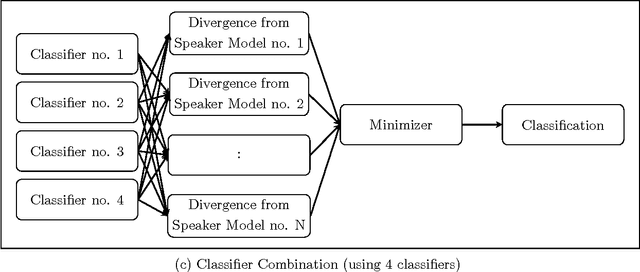
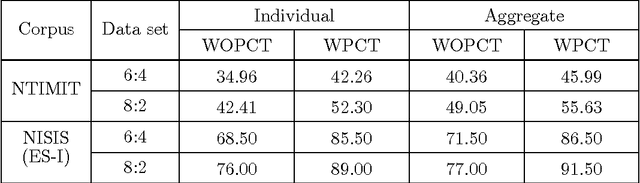
In this work, a novel solution to the speaker identification problem is proposed through minimization of statistical divergences between the probability distribution (g). of feature vectors from the test utterance and the probability distributions of the feature vector corresponding to the speaker classes. This approach is made more robust to the presence of outliers, through the use of suitably modified versions of the standard divergence measures. The relevant solutions to the minimum distance methods are referred to as the minimum rescaled modified distance estimators (MRMDEs). Three measures were considered - the likelihood disparity, the Hellinger distance and Pearson's chi-square distance. The proposed approach is motivated by the observation that, in the case of the likelihood disparity, when the empirical distribution function is used to estimate g, it becomes equivalent to maximum likelihood classification with Gaussian Mixture Models (GMMs) for speaker classes, a highly effective approach used, for example, by Reynolds [22] based on Mel Frequency Cepstral Coefficients (MFCCs) as features. Significant improvement in classification accuracy is observed under this approach on the benchmark speech corpus NTIMIT and a new bilingual speech corpus NISIS, with MFCC features, both in isolation and in combination with delta MFCC features. Moreover, the ubiquitous principal component transformation, by itself and in conjunction with the principle of classifier combination, is found to further enhance the performance.