Fast computation of the TGOSPA metric for multiple target tracking via unbalanced optimal transport

In multiple target tracking, it is important to be able to evaluate the performance of different tracking algorithms. The trajectory generalized optimal sub-pattern assignment metric (TGOSPA) is a recently proposed metric for such evaluations. The TGOSPA metric is computed as the solution to an optimization problem, but for large tracking scenarios, solving this problem becomes computationally demanding. In this paper, we present an approximation algorithm for evaluating the TGOSPA metric, based on casting the TGOSPA problem as an unbalanced multimarginal optimal transport problem. Following recent advances in computational optimal transport, we introduce an entropy regularization and derive an iterative scheme for solving the Lagrangian dual of the regularized problem. Numerical results suggest that our proposed algorithm is more computationally efficient than the alternative of computing the exact metric using a linear programming solver, while still providing an adequate approximation of the metric.

Learning to solve inverse problems using Wasserstein loss

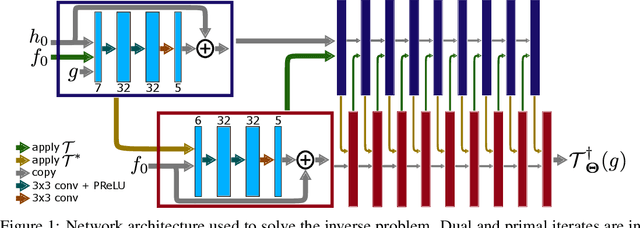
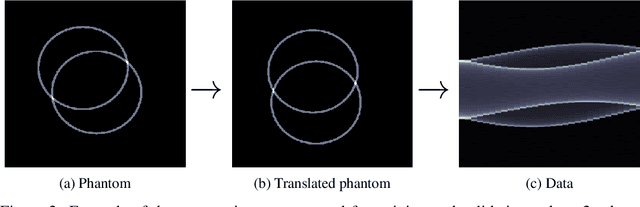
We propose using the Wasserstein loss for training in inverse problems. In particular, we consider a learned primal-dual reconstruction scheme for ill-posed inverse problems using the Wasserstein distance as loss function in the learning. This is motivated by miss-alignments in training data, which when using standard mean squared error loss could severely degrade reconstruction quality. We prove that training with the Wasserstein loss gives a reconstruction operator that correctly compensates for miss-alignments in certain cases, whereas training with the mean squared error gives a smeared reconstruction. Moreover, we demonstrate these effects by training a reconstruction algorithm using both mean squared error and optimal transport loss for a problem in computerized tomography.