Avraham A. Melkman
On the Trade-off between the Number of Nodes and the Number of Trees in a Random Forest
Dec 16, 2023Abstract:In this paper, we focus on the prediction phase of a random forest and study the problem of representing a bag of decision trees using a smaller bag of decision trees, where we only consider binary decision problems on the binary domain and simple decision trees in which an internal node is limited to querying the Boolean value of a single variable. As a main result, we show that the majority function of $n$ variables can be represented by a bag of $T$ ($< n$) decision trees each with polynomial size if $n-T$ is a constant, where $n$ and $T$ must be odd (in order to avoid the tie break). We also show that a bag of $n$ decision trees can be represented by a bag of $T$ decision trees each with polynomial size if $n-T$ is a constant and a small classification error is allowed. A related result on the $k$-out-of-$n$ functions is presented too.
On the Size and Width of the Decoder of a Boolean Threshold Autoencoder
Dec 21, 2021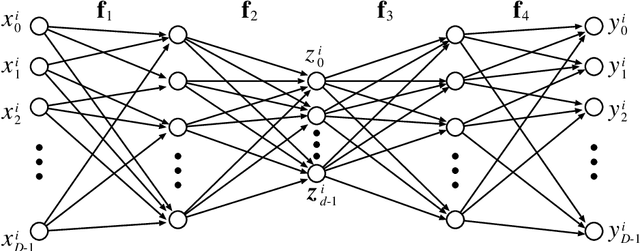
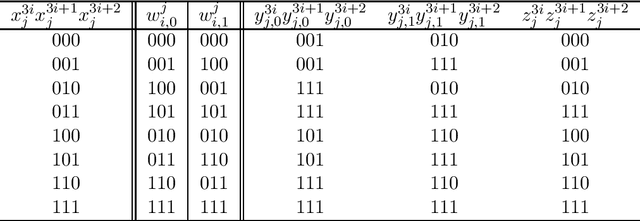
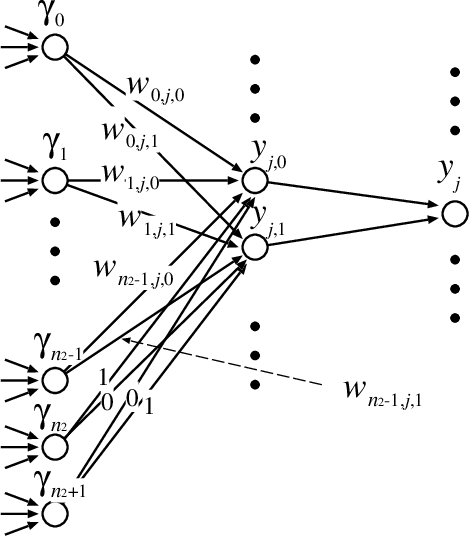
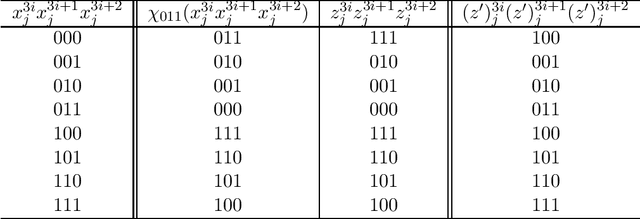
Abstract:In this paper, we study the size and width of autoencoders consisting of Boolean threshold functions, where an autoencoder is a layered neural network whose structure can be viewed as consisting of an encoder, which compresses an input vector to a lower dimensional vector, and a decoder which transforms the low-dimensional vector back to the original input vector exactly (or approximately). We focus on the decoder part, and show that $\Omega(\sqrt{Dn/d})$ and $O(\sqrt{Dn})$ nodes are required to transform $n$ vectors in $d$-dimensional binary space to $D$-dimensional binary space. We also show that the width can be reduced if we allow small errors, where the error is defined as the average of the Hamming distance between each vector input to the encoder part and the resulting vector output by the decoder.
On the Compressive Power of Boolean Threshold Autoencoders
Apr 21, 2020
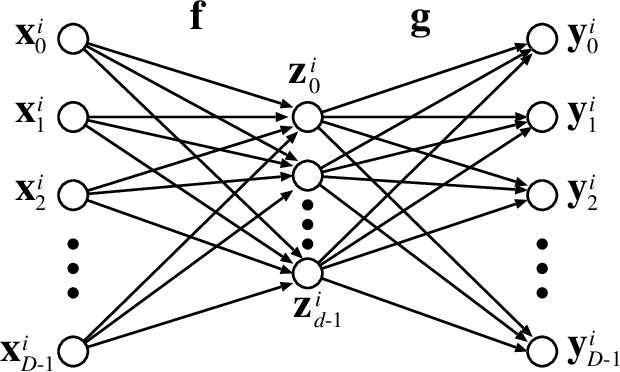
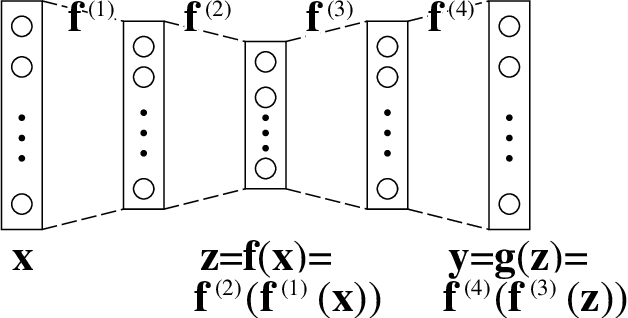
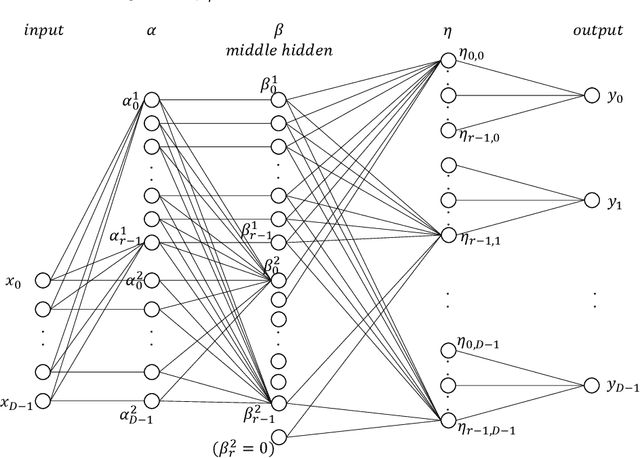
Abstract:An autoencoder is a layered neural network whose structure can be viewed as consisting of an encoder, which compresses an input vector of dimension $D$ to a vector of low dimension $d$, and a decoder which transforms the low-dimensional vector back to the original input vector (or one that is very similar). In this paper we explore the compressive power of autoencoders that are Boolean threshold networks by studying the numbers of nodes and layers that are required to ensure that the numbers of nodes and layers that are required to ensure that each vector in a given set of distinct input binary vectors is transformed back to its original. We show that for any set of $n$ distinct vectors there exists a seven-layer autoencoder with the smallest possible middle layer, (i.e., its size is logarithmic in $n$), but that there is a set of $n$ vectors for which there is no three-layer autoencoder with a middle layer of the same size. In addition we present a kind of trade-off: if a considerably larger middle layer is permissible then a five-layer autoencoder does exist. We also study encoding by itself. The results we obtain suggest that it is the decoding that constitutes the bottleneck of autoencoding. For example, there always is a three-layer Boolean threshold encoder that compresses $n$ vectors into a dimension that is reduced to twice the logarithm of $n$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge