Learning normalizing flows from Entropy-Kantorovich potentials

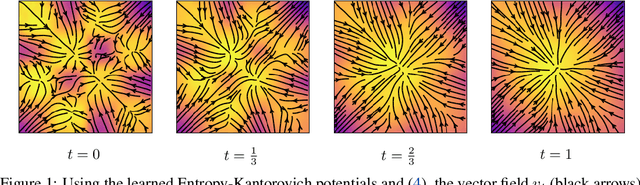
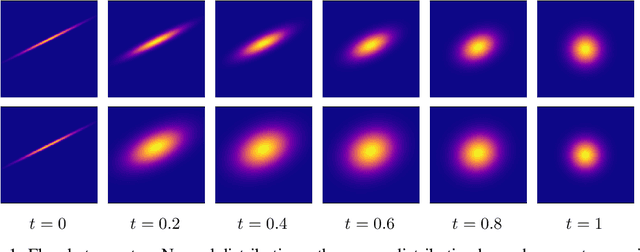
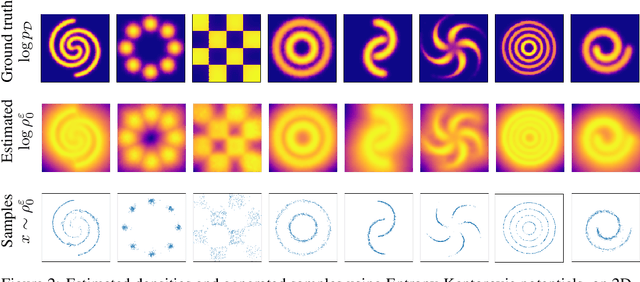
We approach the problem of learning continuous normalizing flows from a dual perspective motivated by entropy-regularized optimal transport, in which continuous normalizing flows are cast as gradients of scalar potential functions. This formulation allows us to train a dual objective comprised only of the scalar potential functions, and removes the burden of explicitly computing normalizing flows during training. After training, the normalizing flow is easily recovered from the potential functions.

Entropy-Regularized $2$-Wasserstein Distance between Gaussian Measures

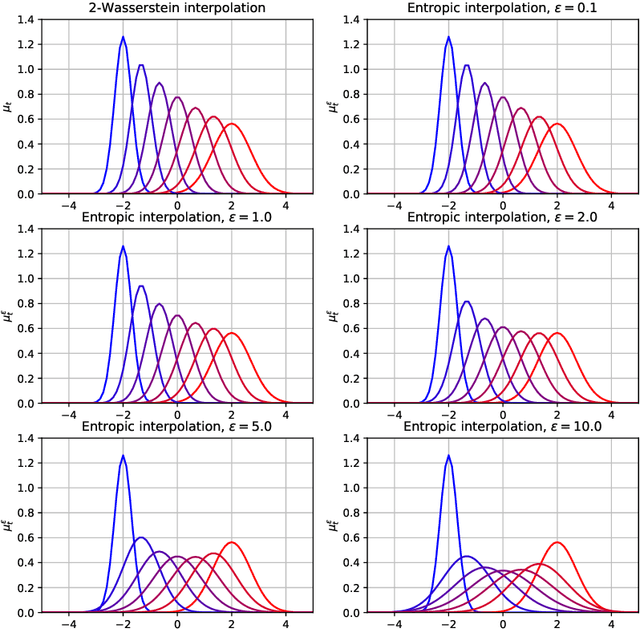
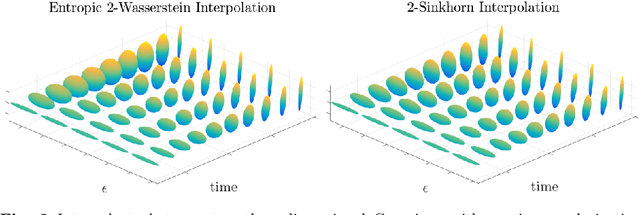
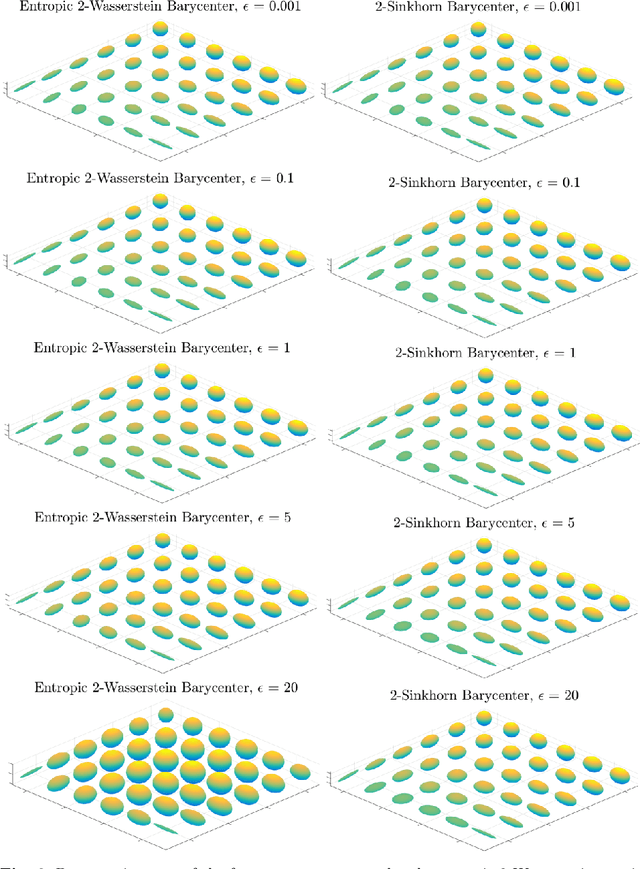
Gaussian distributions are plentiful in applications dealing in uncertainty quantification and diffusivity. They furthermore stand as important special cases for frameworks providing geometries for probability measures, as the resulting geometry on Gaussians is often expressible in closed-form under the frameworks. In this work, we study the Gaussian geometry under the entropy-regularized 2-Wasserstein distance, by providing closed-form solutions for the distance and interpolations between elements. Furthermore, we provide a fixed-point characterization of a population barycenter when restricted to the manifold of Gaussians, which allows computations through the fixed-point iteration algorithm. As a consequence, the results yield closed-form expressions for the 2-Sinkhorn divergence. As the geometries change by varying the regularization magnitude, we study the limiting cases of vanishing and infinite magnitudes, reconfirming well-known results on the limits of the Sinkhorn divergence. Finally, we illustrate the resulting geometries with a numerical study.

How Well Do WGANs Estimate the Wasserstein Metric?

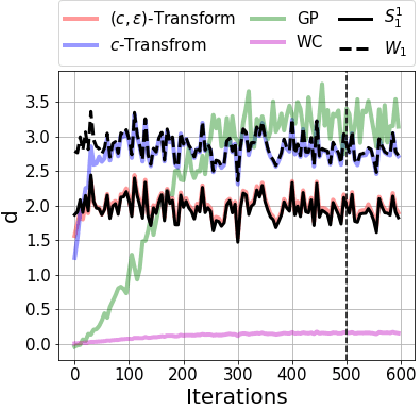
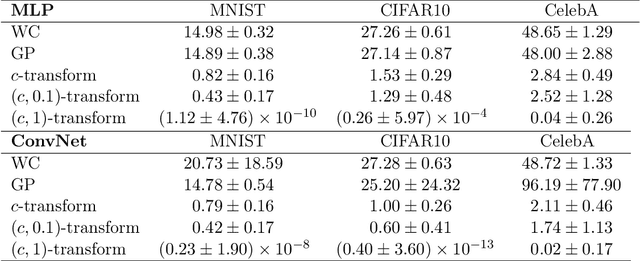
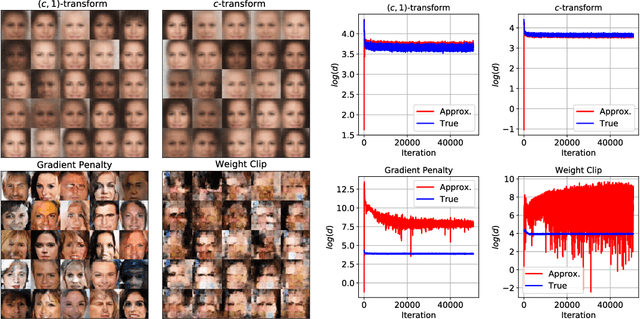
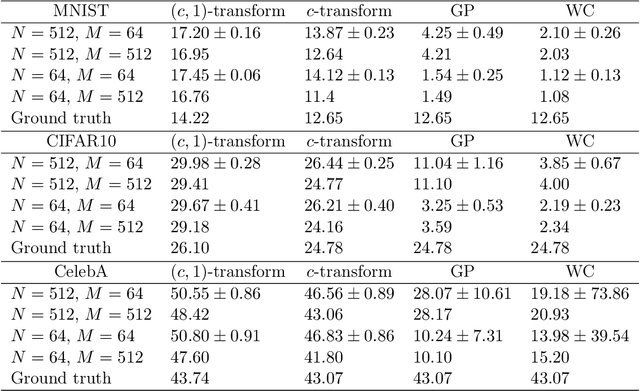
Generative modelling is often cast as minimizing a similarity measure between a data distribution and a model distribution. Recently, a popular choice for the similarity measure has been the Wasserstein metric, which can be expressed in the Kantorovich duality formulation as the optimum difference of the expected values of a potential function under the real data distribution and the model hypothesis. In practice, the potential is approximated with a neural network and is called the discriminator. Duality constraints on the function class of the discriminator are enforced approximately, and the expectations are estimated from samples. This gives at least three sources of errors: the approximated discriminator and constraints, the estimation of the expectation value, and the optimization required to find the optimal potential. In this work, we study how well the methods, that are used in generative adversarial networks to approximate the Wasserstein metric, perform. We consider, in particular, the $c$-transform formulation, which eliminates the need to enforce the constraints explicitly. We demonstrate that the $c$-transform allows for a more accurate estimation of the true Wasserstein metric from samples, but surprisingly, does not perform the best in the generative setting.