Cumulative Learning Rate Adaptation: Revisiting Path-Based Schedules for SGD and Adam

The learning rate is a crucial hyperparameter in deep learning, with its ideal value depending on the problem and potentially changing during training. In this paper, we investigate the practical utility of adaptive learning rate mechanisms that adjust step sizes dynamically in response to the loss landscape. We revisit a cumulative path-based adaptation scheme proposed in 2017, which adjusts the learning rate based on the discrepancy between the observed path length, computed as a time-discounted sum of normalized gradient steps, and the expected length of a random walk. While the original approach offers a compelling intuition, we show that its adaptation mechanism for Adam is conceptually inconsistent due to the optimizer's internal preconditioning. We propose a corrected variant that better reflects Adam's update dynamics. To assess the practical value of online learning rate adaptation, we benchmark SGD and Adam, with and without cumulative adaptation, and compare them to a recent alternative method. Our results aim to clarify when and why such adaptive strategies offer practical benefits.

Solving a Real-World Optimization Problem Using Proximal Policy Optimization with Curriculum Learning and Reward Engineering

We present a proximal policy optimization (PPO) agent trained through curriculum learning (CL) principles and meticulous reward engineering to optimize a real-world high-throughput waste sorting facility. Our work addresses the challenge of effectively balancing the competing objectives of operational safety, volume optimization, and minimizing resource usage. A vanilla agent trained from scratch on these multiple criteria fails to solve the problem due to its inherent complexities. This problem is particularly difficult due to the environment's extremely delayed rewards with long time horizons and class (or action) imbalance, with important actions being infrequent in the optimal policy. This forces the agent to anticipate long-term action consequences and prioritize rare but rewarding behaviours, creating a non-trivial reinforcement learning task. Our five-stage CL approach tackles these challenges by gradually increasing the complexity of the environmental dynamics during policy transfer while simultaneously refining the reward mechanism. This iterative and adaptable process enables the agent to learn a desired optimal policy. Results demonstrate that our approach significantly improves inference-time safety, achieving near-zero safety violations in addition to enhancing waste sorting plant efficiency.

ContainerGym: A Real-World Reinforcement Learning Benchmark for Resource Allocation

We present ContainerGym, a benchmark for reinforcement learning inspired by a real-world industrial resource allocation task. The proposed benchmark encodes a range of challenges commonly encountered in real-world sequential decision making problems, such as uncertainty. It can be configured to instantiate problems of varying degrees of difficulty, e.g., in terms of variable dimensionality. Our benchmark differs from other reinforcement learning benchmarks, including the ones aiming to encode real-world difficulties, in that it is directly derived from a real-world industrial problem, which underwent minimal simplification and streamlining. It is sufficiently versatile to evaluate reinforcement learning algorithms on any real-world problem that fits our resource allocation framework. We provide results of standard baseline methods. Going beyond the usual training reward curves, our results and the statistical tools used to interpret them allow to highlight interesting limitations of well-known deep reinforcement learning algorithms, namely PPO, TRPO and DQN.

Convex Optimization with an Interpolation-based Projection and its Application to Deep Learning

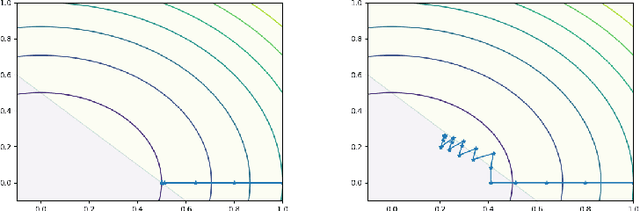
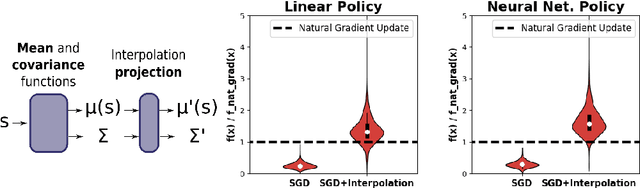
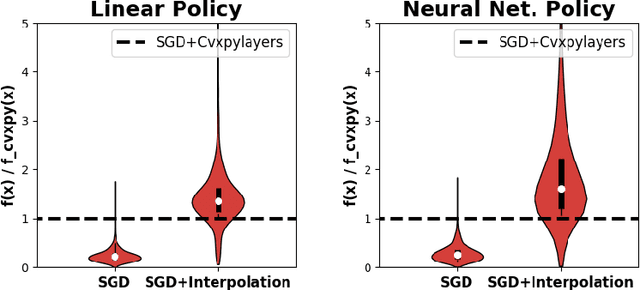
Convex optimizers have known many applications as differentiable layers within deep neural architectures. One application of these convex layers is to project points into a convex set. However, both forward and backward passes of these convex layers are significantly more expensive to compute than those of a typical neural network. We investigate in this paper whether an inexact, but cheaper projection, can drive a descent algorithm to an optimum. Specifically, we propose an interpolation-based projection that is computationally cheap and easy to compute given a convex, domain defining, function. We then propose an optimization algorithm that follows the gradient of the composition of the objective and the projection and prove its convergence for linear objectives and arbitrary convex and Lipschitz domain defining inequality constraints. In addition to the theoretical contributions, we demonstrate empirically the practical interest of the interpolation projection when used in conjunction with neural networks in a reinforcement learning and a supervised learning setting.