Near-Efficient and Non-Asymptotic Multiway Inference

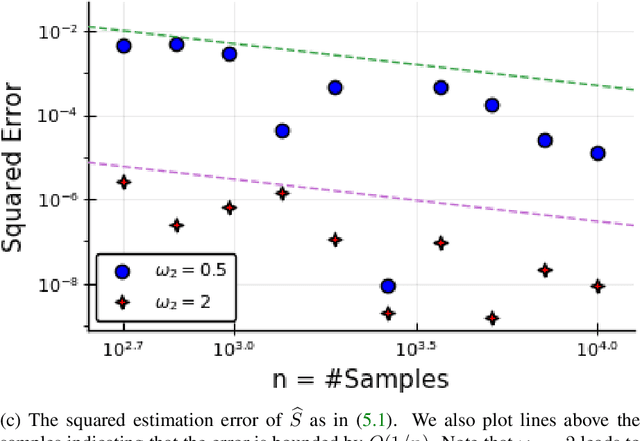
We establish non-asymptotic efficiency guarantees for tensor decomposition-based inference in count data models. Under a Poisson framework, we consider two related goals: (i) parametric inference, the estimation of the full distributional parameter tensor, and (ii) multiway analysis, the recovery of its canonical polyadic (CP) decomposition factors. Our main result shows that in the rank-one setting, a rank-constrained maximum-likelihood estimator achieves multiway analysis with variance matching the Cram\'{e}r-Rao Lower Bound (CRLB) up to absolute constants and logarithmic factors. This provides a general framework for studying "near-efficient" multiway estimators in finite-sample settings. For higher ranks, we illustrate that our multiway estimator may not attain the CRLB; nevertheless, CP-based parametric inference remains nearly minimax optimal, with error bounds that improve on prior work by offering more favorable dependence on the CP rank. Numerical experiments corroborate near-efficiency in the rank-one case and highlight the efficiency gap in higher-rank scenarios.

A Latent-Variable Formulation of the Poisson Canonical Polyadic Tensor Model: Maximum Likelihood Estimation and Fisher Information

We establish parameter inference for the Poisson canonical polyadic (PCP) tensor model through a latent-variable formulation. Our approach exploits the observation that any random PCP tensor can be derived by marginalizing an unobservable random tensor of one dimension larger. The loglikelihood of this larger dimensional tensor, referred to as the "complete" loglikelihood, is comprised of multiple rank one PCP loglikelihoods. Using this methodology, we first derive non-iterative maximum likelihood estimators for the PCP model and demonstrate that several existing algorithms for fitting non-negative matrix and tensor factorizations are Expectation-Maximization algorithms. Next, we derive the observed and expected Fisher information matrices for the PCP model. The Fisher information provides us crucial insights into the well-posedness of the tensor model, such as the role that tensor rank plays in identifiability and indeterminacy. For the special case of rank one PCP models, we demonstrate that these results are greatly simplified.

Sliding Window Informative Canonical Correlation Analysis

Canonical correlation analysis (CCA) is a technique for finding correlated sets of features between two datasets. In this paper, we propose a novel extension of CCA to the online, streaming data setting: Sliding Window Informative Canonical Correlation Analysis (SWICCA). Our method uses a streaming principal component analysis (PCA) algorithm as a backend and uses these outputs combined with a small sliding window of samples to estimate the CCA components in real time. We motivate and describe our algorithm, provide numerical simulations to characterize its performance, and provide a theoretical performance guarantee. The SWICCA method is applicable and scalable to extremely high dimensions, and we provide a real-data example that demonstrates this capability.

Sparse Equisigned PCA: Algorithms and Performance Bounds in the Noisy Rank-1 Setting

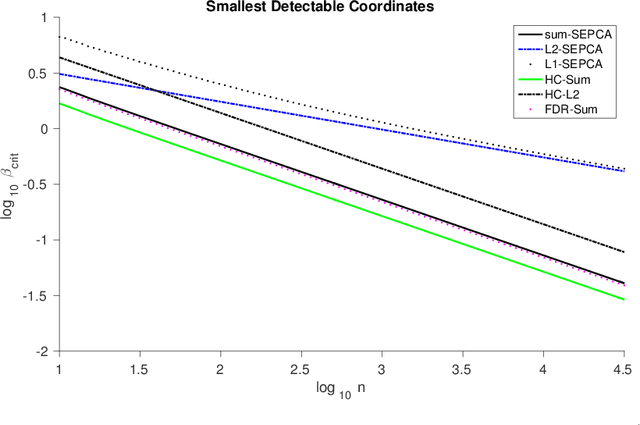
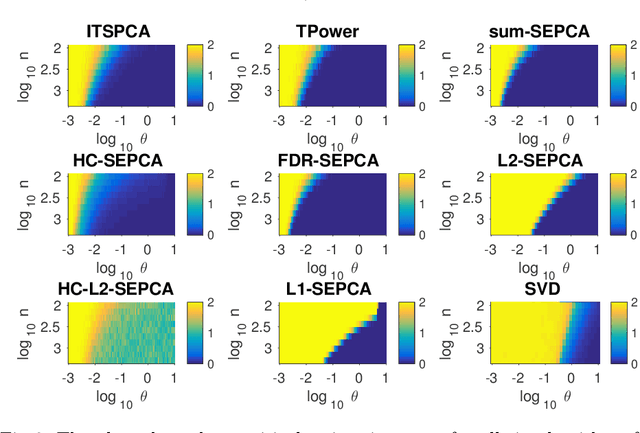
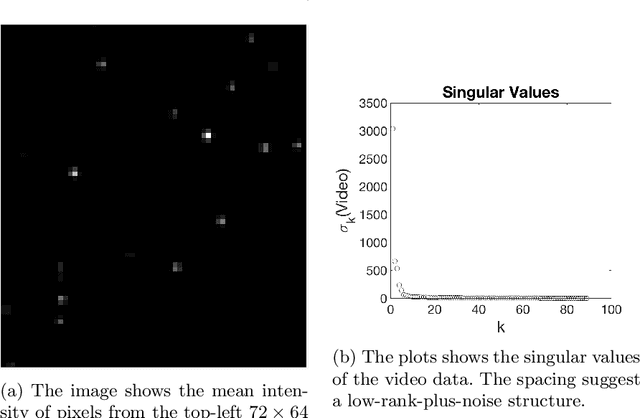
Singular value decomposition (SVD) based principal component analysis (PCA) breaks down in the high-dimensional and limited sample size regime below a certain critical eigen-SNR that depends on the dimensionality of the system and the number of samples. Below this critical eigen-SNR, the estimates returned by the SVD are asymptotically uncorrelated with the latent principal components. We consider a setting where the left singular vector of the underlying rank one signal matrix is assumed to be sparse and the right singular vector is assumed to be equisigned, that is, having either only nonnegative or only nonpositive entries. We consider six different algorithms for estimating the sparse principal component based on different statistical criteria and prove that by exploiting sparsity, we recover consistent estimates in the low eigen-SNR regime where the SVD fails. Our analysis reveals conditions under which a coordinate selection scheme based on a \textit{sum-type decision statistic} outperforms schemes that utilize the $\ell_1$ and $\ell_2$ norm-based statistics. We derive lower bounds on the size of detectable coordinates of the principal left singular vector and utilize these lower bounds to derive lower bounds on the worst-case risk. Finally, we verify our findings with numerical simulations and illustrate the performance with a video data example, where the interest is in identifying objects.

Time Series Source Separation using Dynamic Mode Decomposition

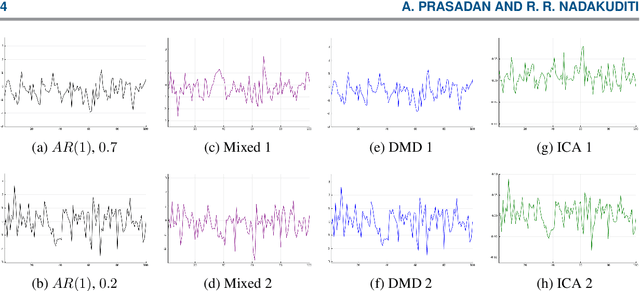
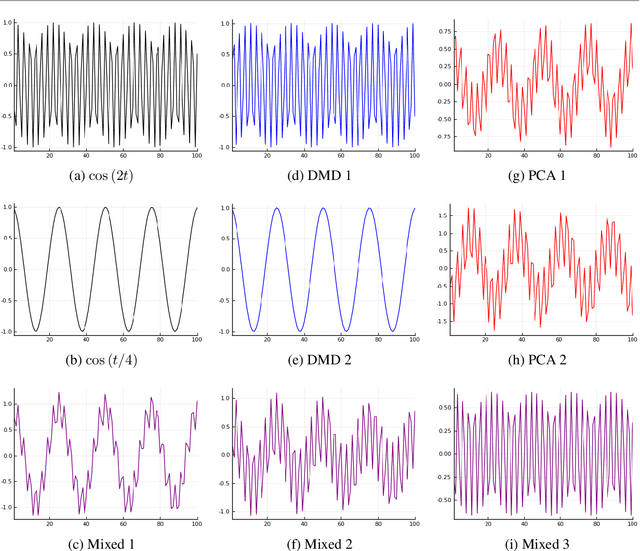
The dynamic mode decomposition (DMD) extracted dynamic modes are the non-orthogonal eigenvectors of the matrix that best approximates the one-step temporal evolution of the multivariate samples. In the context of dynamic system analysis, the extracted dynamic modes are a generalization of global stability modes. We apply DMD to a data matrix whose rows are linearly independent, additive mixtures of latent time series. We show that when the latent time series are uncorrelated at a lag of one time-step then, in the large sample limit, the recovered dynamic modes will approximate, up to a column-wise normalization, the columns of the mixing matrix. Thus, DMD is a time series blind source separation algorithm in disguise, but is different from closely related second order algorithms such as SOBI and AMUSE. All can unmix mixed ergodic Gaussian time series in a way that ICA fundamentally cannot. We use our insights on single lag DMD to develop a higher-lag extension, analyze the finite sample performance with and without randomly missing data, and identify settings where the higher lag variant can outperform the conventional single lag variant. We validate our results with numerical simulations, and highlight how DMD can be used in change point detection.