Quantum Sparse Recovery and Quantum Orthogonal Matching Pursuit

We study quantum sparse recovery in non-orthogonal, overcomplete dictionaries: given coherent quantum access to a state and a dictionary of vectors, the goal is to reconstruct the state up to $\ell_2$ error using as few vectors as possible. We first show that the general recovery problem is NP-hard, ruling out efficient exact algorithms in full generality. To overcome this, we introduce Quantum Orthogonal Matching Pursuit (QOMP), the first quantum analogue of the classical OMP greedy algorithm. QOMP combines quantum subroutines for inner product estimation, maximum finding, and block-encoded projections with an error-resetting design that avoids iteration-to-iteration error accumulation. Under standard mutual incoherence and well-conditioned sparsity assumptions, QOMP provably recovers the exact support of a $K$-sparse state in polynomial time. As an application, we give the first framework for sparse quantum tomography with non-orthogonal dictionaries in $\ell_2$ norm, achieving query complexity $\widetilde{O}(\sqrt{N}/\epsilon)$ in favorable regimes and reducing tomography to estimating only $K$ coefficients instead of $N$ amplitudes. In particular, for pure-state tomography with $m=O(N)$ dictionary vectors and sparsity $K=\widetilde{O}(1)$ on a well-conditioned subdictionary, this circumvents the $\widetilde{\Omega}(N/\epsilon)$ lower bound that holds in the dense, orthonormal-dictionary setting, without contradiction, by leveraging sparsity together with non-orthogonality. Beyond tomography, we analyze QOMP in the QRAM model, where it yields polynomial speedups over classical OMP implementations, and provide a quantum algorithm to estimate the mutual incoherence of a dictionary of $m$ vectors in $O(m/\epsilon)$ queries, improving over both deterministic and quantum-inspired classical methods.

The Generalized Skew Spectrum of Graphs

This paper proposes a family of permutation-invariant graph embeddings, generalizing the Skew Spectrum of graphs of Kondor & Borgwardt (2008). Grounded in group theory and harmonic analysis, our method introduces a new class of graph invariants that are isomorphism-invariant and capable of embedding richer graph structures - including attributed graphs, multilayer graphs, and hypergraphs - which the Skew Spectrum could not handle. Our generalization further defines a family of functions that enables a trade-off between computational complexity and expressivity. By applying generalization-preserving heuristics to this family, we improve the Skew Spectrum's expressivity at the same computational cost. We formally prove the invariance of our generalization, demonstrate its improved expressiveness through experiments, and discuss its efficient computation.

Quantum Algorithms for Data Representation and Analysis

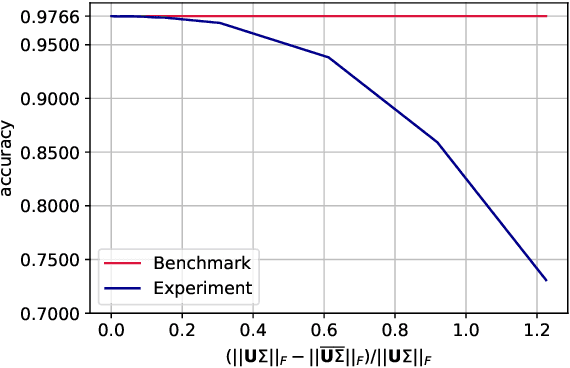
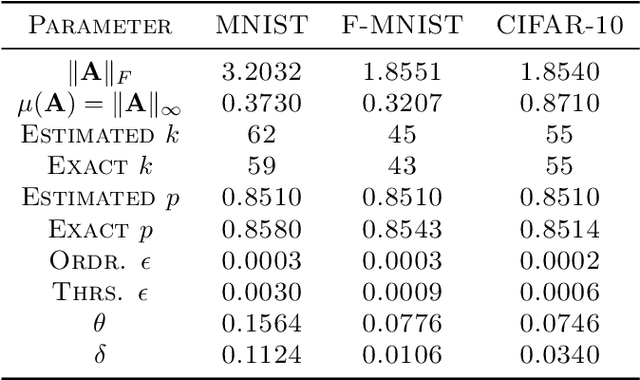
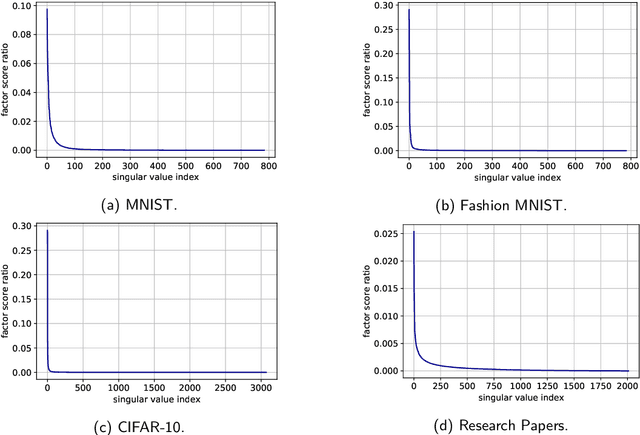
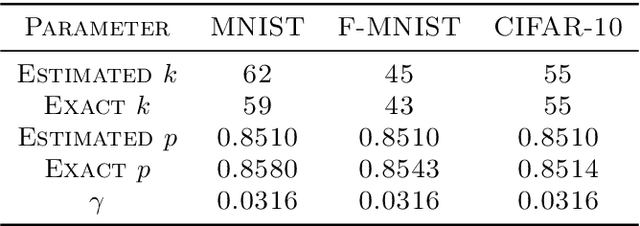
We narrow the gap between previous literature on quantum linear algebra and useful data analysis on a quantum computer, providing quantum procedures that speed-up the solution of eigenproblems for data representation in machine learning. The power and practical use of these subroutines is shown through new quantum algorithms, sublinear in the input matrix's size, for principal component analysis, correspondence analysis, and latent semantic analysis. We provide a theoretical analysis of the run-time and prove tight bounds on the randomized algorithms' error. We run experiments on multiple datasets, simulating PCA's dimensionality reduction for image classification with the novel routines. The results show that the run-time parameters that do not depend on the input's size are reasonable and that the error on the computed model is small, allowing for competitive classification performances.