The Differentiable Feasibility Pump

Although nearly 20 years have passed since its conception, the feasibility pump algorithm remains a widely used heuristic to find feasible primal solutions to mixed-integer linear problems. Many extensions of the initial algorithm have been proposed. Yet, its core algorithm remains centered around two key steps: solving the linear relaxation of the original problem to obtain a solution that respects the constraints, and rounding it to obtain an integer solution. This paper shows that the traditional feasibility pump and many of its follow-ups can be seen as gradient-descent algorithms with specific parameters. A central aspect of this reinterpretation is observing that the traditional algorithm differentiates the solution of the linear relaxation with respect to its cost. This reinterpretation opens many opportunities for improving the performance of the original algorithm. We study how to modify the gradient-update step as well as extending its loss function. We perform extensive experiments on MIPLIB instances and show that these modifications can substantially reduce the number of iterations needed to find a solution.

The Algorithm Configuration Problem

The field of algorithmic optimization has significantly advanced with the development of methods for the automatic configuration of algorithmic parameters. This article delves into the Algorithm Configuration Problem, focused on optimizing parametrized algorithms for solving specific instances of decision/optimization problems. We present a comprehensive framework that not only formalizes the Algorithm Configuration Problem, but also outlines different approaches for its resolution, leveraging machine learning models and heuristic strategies. The article categorizes existing methodologies into per-instance and per-problem approaches, distinguishing between offline and online strategies for model construction and deployment. By synthesizing these approaches, we aim to provide a clear pathway for both understanding and addressing the complexities inherent in algorithm configuration.

Learning to Configure Mathematical Programming Solvers by Mathematical Programming

We discuss the issue of finding a good mathematical programming solver configuration for a particular instance of a given problem, and we propose a two-phase approach to solve it. In the first phase we learn the relationships between the instance, the configuration and the performance of the configured solver on the given instance. A specific difficulty of learning a good solver configuration is that parameter settings may not all be independent; this requires enforcing (hard) constraints, something that many widely used supervised learning methods cannot natively achieve. We tackle this issue in the second phase of our approach, where we use the learnt information to construct and solve an optimization problem having an explicit representation of the dependency/consistency constraints on the configuration parameter settings. We discuss computational results for two different instantiations of this approach on a unit commitment problem arising in the short-term planning of hydro valleys. We use logistic regression as the supervised learning methodology and consider CPLEX as the solver of interest.

A learning-based mathematical programming formulation for the automatic configuration of optimization solvers

We propose a methodology, based on machine learning and optimization, for selecting a solver configuration for a given instance. First, we employ a set of solved instances and configurations in order to learn a performance function of the solver. Secondly, we formulate a mixed-integer nonlinear program where the objective/constraints explicitly encode the learnt information, and which we solve, upon the arrival of an unknown instance, to find the best solver configuration for that instance, based on the performance function. The main novelty of our approach lies in the fact that the configuration set search problem is formulated as a mathematical program, which allows us to a) enforce hard dependence and compatibility constraints on the configurations, and b) solve it efficiently with off-the-shelf optimization tools.

Structured Pruning of Neural Networks for Constraints Learning

In recent years, the integration of Machine Learning (ML) models with Operation Research (OR) tools has gained popularity across diverse applications, including cancer treatment, algorithmic configuration, and chemical process optimization. In this domain, the combination of ML and OR often relies on representing the ML model output using Mixed Integer Programming (MIP) formulations. Numerous studies in the literature have developed such formulations for many ML predictors, with a particular emphasis on Artificial Neural Networks (ANNs) due to their significant interest in many applications. However, ANNs frequently contain a large number of parameters, resulting in MIP formulations that are impractical to solve, thereby impeding scalability. In fact, the ML community has already introduced several techniques to reduce the parameter count of ANNs without compromising their performance, since the substantial size of modern ANNs presents challenges for ML applications as it significantly impacts computational efforts during training and necessitates significant memory resources for storage. In this paper, we showcase the effectiveness of pruning, one of these techniques, when applied to ANNs prior to their integration into MIPs. By pruning the ANN, we achieve significant improvements in the speed of the solution process. We discuss why pruning is more suitable in this context compared to other ML compression techniques, and we identify the most appropriate pruning strategies. To highlight the potential of this approach, we conduct experiments using feed-forward neural networks with multiple layers to construct adversarial examples. Our results demonstrate that pruning offers remarkable reductions in solution times without hindering the quality of the final decision, enabling the resolution of previously unsolvable instances.

On the Convergence of Stochastic Gradient Descent in Low-precision Number Formats

Deep learning models are dominating almost all artificial intelligence tasks such as vision, text, and speech processing. Stochastic Gradient Descent (SGD) is the main tool for training such models, where the computations are usually performed in single-precision floating-point number format. The convergence of single-precision SGD is normally aligned with the theoretical results of real numbers since they exhibit negligible error. However, the numerical error increases when the computations are performed in low-precision number formats. This provides compelling reasons to study the SGD convergence adapted for low-precision computations. We present both deterministic and stochastic analysis of the SGD algorithm, obtaining bounds that show the effect of number format. Such bounds can provide guidelines as to how SGD convergence is affected when constraints render the possibility of performing high-precision computations remote.

Deep Neural Networks pruning via the Structured Perspective Regularization

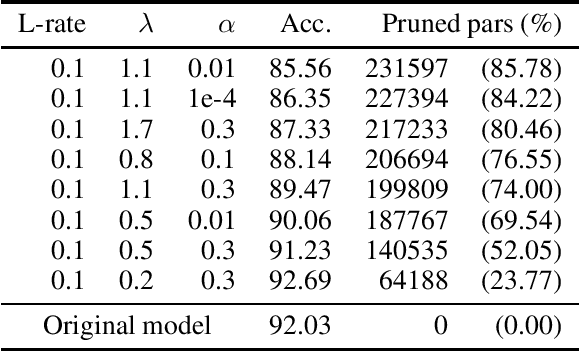
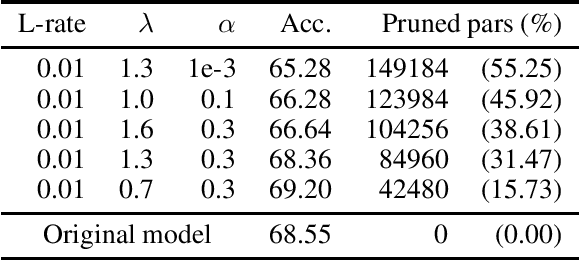
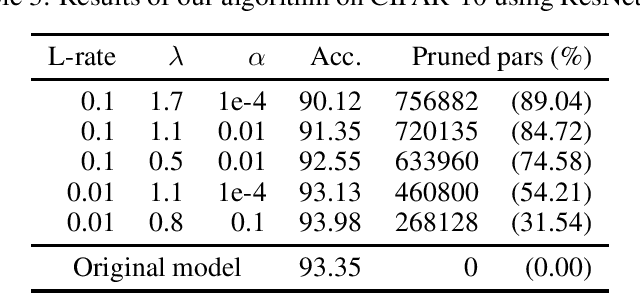
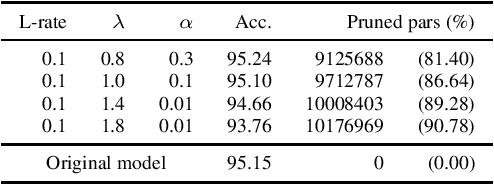
In Machine Learning, Artificial Neural Networks (ANNs) are a very powerful tool, broadly used in many applications. Often, the selected (deep) architectures include many layers, and therefore a large amount of parameters, which makes training, storage and inference expensive. This motivated a stream of research about compressing the original networks into smaller ones without excessively sacrificing performances. Among the many proposed compression approaches, one of the most popular is \emph{pruning}, whereby entire elements of the ANN (links, nodes, channels, \ldots) and the corresponding weights are deleted. Since the nature of the problem is inherently combinatorial (what elements to prune and what not), we propose a new pruning method based on Operational Research tools. We start from a natural Mixed-Integer-Programming model for the problem, and we use the Perspective Reformulation technique to strengthen its continuous relaxation. Projecting away the indicator variables from this reformulation yields a new regularization term, which we call the Structured Perspective Regularization, that leads to structured pruning of the initial architecture. We test our method on some ResNet architectures applied to CIFAR-10, CIFAR-100 and ImageNet datasets, obtaining competitive performances w.r.t.~the state of the art for structured pruning.