MF-OML: Online Mean-Field Reinforcement Learning with Occupation Measures for Large Population Games

Reinforcement learning for multi-agent games has attracted lots of attention recently. However, given the challenge of solving Nash equilibria for large population games, existing works with guaranteed polynomial complexities either focus on variants of zero-sum and potential games, or aim at solving (coarse) correlated equilibria, or require access to simulators, or rely on certain assumptions that are hard to verify. This work proposes MF-OML (Mean-Field Occupation-Measure Learning), an online mean-field reinforcement learning algorithm for computing approximate Nash equilibria of large population sequential symmetric games. MF-OML is the first fully polynomial multi-agent reinforcement learning algorithm for provably solving Nash equilibria (up to mean-field approximation gaps that vanish as the number of players $N$ goes to infinity) beyond variants of zero-sum and potential games. When evaluated by the cumulative deviation from Nash equilibria, the algorithm is shown to achieve a high probability regret bound of $\tilde{O}(M^{3/4}+N^{-1/2}M)$ for games with the strong Lasry-Lions monotonicity condition, and a regret bound of $\tilde{O}(M^{11/12}+N^{- 1/6}M)$ for games with only the Lasry-Lions monotonicity condition, where $M$ is the total number of episodes and $N$ is the number of agents of the game. As a byproduct, we also obtain the first tractable globally convergent computational algorithm for computing approximate Nash equilibria of monotone mean-field games.

Theoretical Guarantees of Fictitious Discount Algorithms for Episodic Reinforcement Learning and Global Convergence of Policy Gradient Methods

When designing algorithms for finite-time-horizon episodic reinforcement learning problems, a common approach is to introduce a fictitious discount factor and use stationary policies for approximations. Empirically, it has been shown that the fictitious discount factor helps reduce variance, and stationary policies serve to save the per-iteration computational cost. Theoretically, however, there is no existing work on convergence analysis for algorithms with this fictitious discount recipe. This paper takes the first step towards analyzing these algorithms. It focuses on two vanilla policy gradient (VPG) variants: the first being a widely used variant with discounted advantage estimations (DAE), the second with an additional fictitious discount factor in the score functions of the policy gradient estimators. Non-asymptotic convergence guarantees are established for both algorithms, and the additional discount factor is shown to reduce the bias introduced in DAE and thus improve the algorithm convergence asymptotically. A key ingredient of our analysis is to connect three settings of Markov decision processes (MDPs): the finite-time-horizon, the average reward and the discounted settings. To our best knowledge, this is the first theoretical guarantee on fictitious discount algorithms for the episodic reinforcement learning of finite-time-horizon MDPs, which also leads to the (first) global convergence of policy gradient methods for finite-time-horizon episodic reinforcement learning.

Reinforcement learning for linear-convex models with jumps via stability analysis of feedback controls

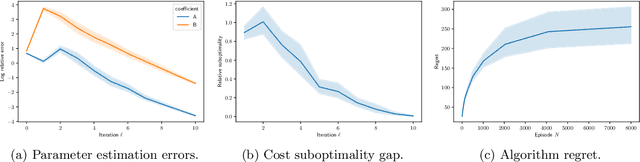
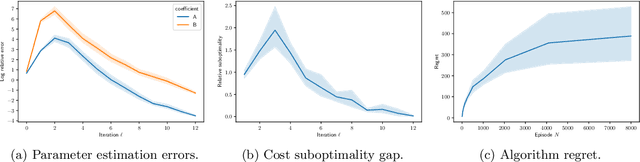
We study finite-time horizon continuous-time linear-convex reinforcement learning problems in an episodic setting. In this problem, the unknown linear jump-diffusion process is controlled subject to nonsmooth convex costs. We show that the associated linear-convex control problems admit Lipchitz continuous optimal feedback controls and further prove the Lipschitz stability of the feedback controls, i.e., the performance gap between applying feedback controls for an incorrect model and for the true model depends Lipschitz-continuously on the magnitude of perturbations in the model coefficients; the proof relies on a stability analysis of the associated forward-backward stochastic differential equation. We then propose a novel least-squares algorithm which achieves a regret of the order $O(\sqrt{N\ln N})$ on linear-convex learning problems with jumps, where $N$ is the number of learning episodes; the analysis leverages the Lipschitz stability of feedback controls and concentration properties of sub-Weibull random variables.

A General Framework for Learning Mean-Field Games

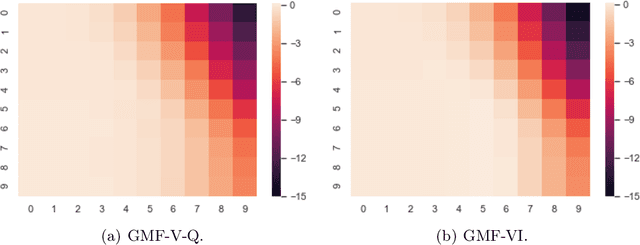
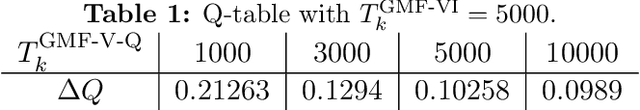
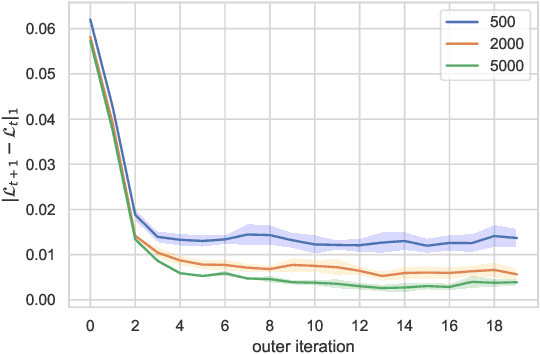
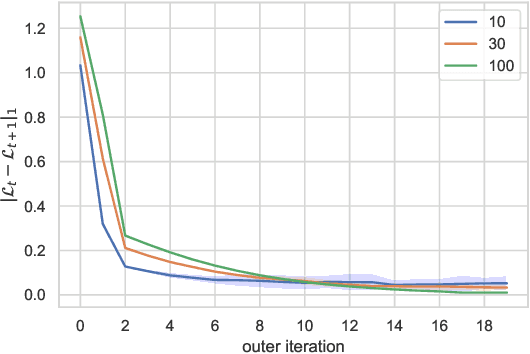
This paper presents a general mean-field game (GMFG) framework for simultaneous learning and decision-making in stochastic games with a large population. It first establishes the existence of a unique Nash Equilibrium to this GMFG, and demonstrates that naively combining Q-learning with the fixed-point approach in classical MFGs yields unstable algorithms. It then proposes value-based and policy-based reinforcement learning algorithms (GMF-P and GMF-P respectively) with smoothed policies, with analysis of convergence property and computational complexity. The experiments on repeated Ad auction problems demonstrate that GMF-V-Q, a specific GMF-V algorithm based on Q-learning, is efficient and robust in terms of convergence and learning accuracy. Moreover, its performance is superior in convergence, stability, and learning ability, when compared with existing algorithms for multi-agent reinforcement learning.