Expressive Priors in Bayesian Neural Networks: Kernel Combinations and Periodic Functions

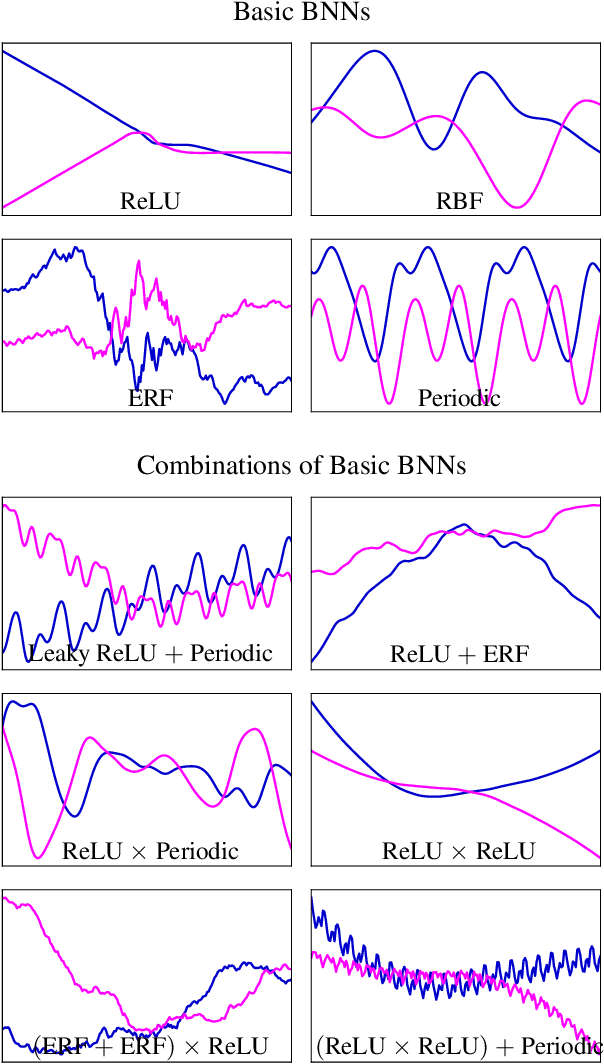
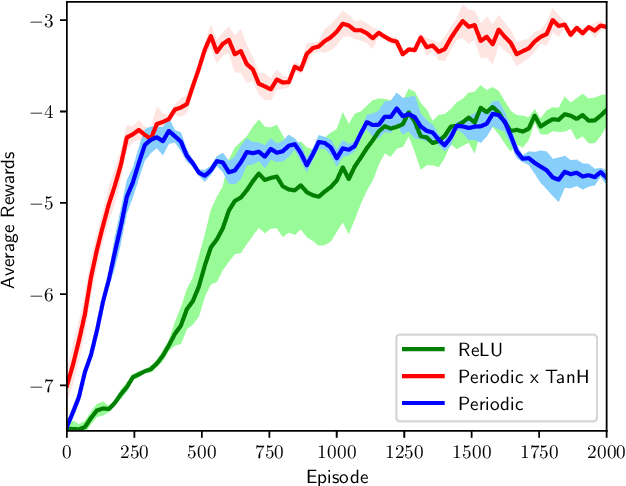
A simple, flexible approach to creating expressive priors in Gaussian process (GP) models makes new kernels from a combination of basic kernels, e.g. summing a periodic and linear kernel can capture seasonal variation with a long term trend. Despite a well-studied link between GPs and Bayesian neural networks (BNNs), the BNN analogue of this has not yet been explored. This paper derives BNN architectures mirroring such kernel combinations. Furthermore, it shows how BNNs can produce periodic kernels, which are often useful in this context. These ideas provide a principled approach to designing BNNs that incorporate prior knowledge about a function. We showcase the practical value of these ideas with illustrative experiments in supervised and reinforcement learning settings.

Bayesian Neural Network Ensembles

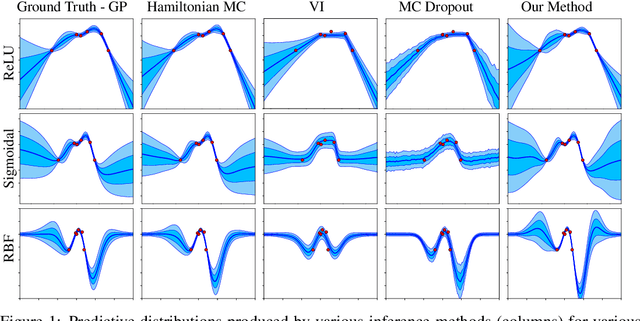
Ensembles of neural networks (NNs) have long been used to estimate predictive uncertainty; a small number of NNs are trained from different initialisations and sometimes on differing versions of the dataset. The variance of the ensemble's predictions is interpreted as its epistemic uncertainty. The appeal of ensembling stems from being a collection of regular NNs - this makes them both scalable and easily implementable. They have achieved strong empirical results in recent years, often presented as a practical alternative to more costly Bayesian NNs (BNNs). The departure from Bayesian methodology is of concern since the Bayesian framework provides a principled, widely-accepted approach to handling uncertainty. In this extended abstract we derive and implement a modified NN ensembling scheme, which provides a consistent estimator of the Bayesian posterior in wide NNs - regularising parameters about values drawn from a prior distribution.

Bayesian Inference with Anchored Ensembles of Neural Networks, and Application to Exploration in Reinforcement Learning

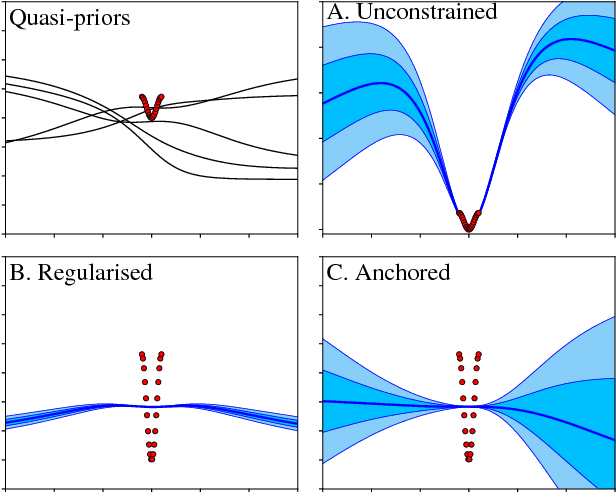
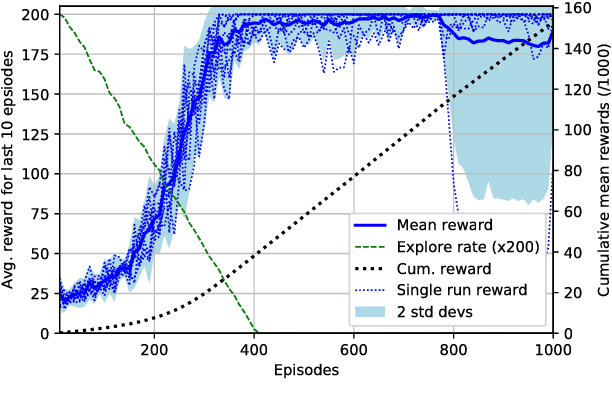
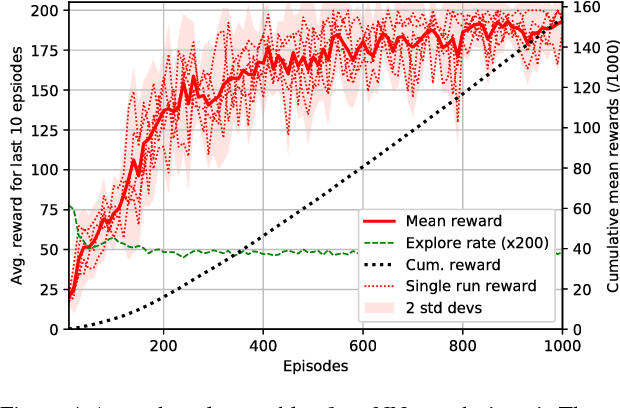
The use of ensembles of neural networks (NNs) for the quantification of predictive uncertainty is widespread. However, the current justification is intuitive rather than analytical. This work proposes one minor modification to the normal ensembling methodology, which we prove allows the ensemble to perform Bayesian inference, hence converging to the corresponding Gaussian Process as both the total number of NNs, and the size of each, tend to infinity. This working paper provides early-stage results in a reinforcement learning setting, analysing the practicality of the technique for an ensemble of small, finite number. Using the uncertainty estimates produced by anchored ensembles to govern the exploration-exploitation process results in steadier, more stable learning.

High-Quality Prediction Intervals for Deep Learning: A Distribution-Free, Ensembled Approach

This paper considers the generation of prediction intervals (PIs) by neural networks for quantifying uncertainty in regression tasks. It is axiomatic that high-quality PIs should be as narrow as possible, whilst capturing a specified portion of data. We derive a loss function directly from this axiom that requires no distributional assumption. We show how its form derives from a likelihood principle, that it can be used with gradient descent, and that model uncertainty is accounted for in ensembled form. Benchmark experiments show the method outperforms current state-of-the-art uncertainty quantification methods, reducing average PI width by over 10%.