Learning optimal wavelet bases using a neural network approach

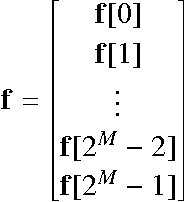
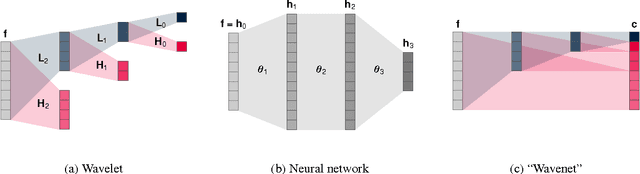
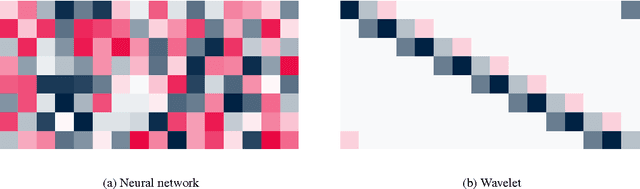
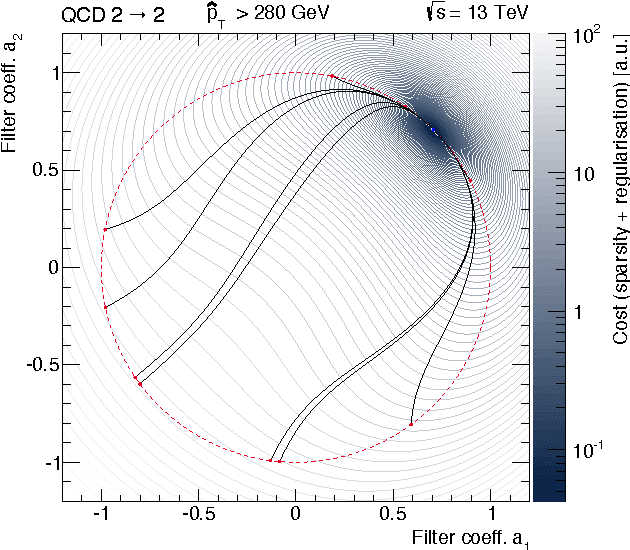
A novel method for learning optimal, orthonormal wavelet bases for representing 1- and 2D signals, based on parallels between the wavelet transform and fully connected artificial neural networks, is described. The structural similarities between these two concepts are reviewed and combined to a "wavenet", allowing for the direct learning of optimal wavelet filter coefficient through stochastic gradient descent with back-propagation over ensembles of training inputs, where conditions on the filter coefficients for constituting orthonormal wavelet bases are cast as quadratic regularisations terms. We describe the practical implementation of this method, and study its performance for high-energy physics collision events for QCD $2 \to 2$ processes. It is shown that an optimal solution is found, even in a high-dimensional search space, and the implications of the result are discussed.

Decorrelated Jet Substructure Tagging using Adversarial Neural Networks

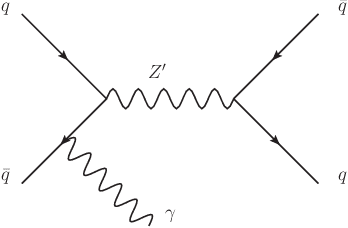
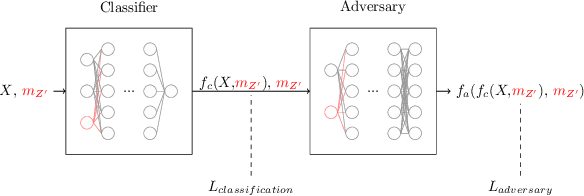
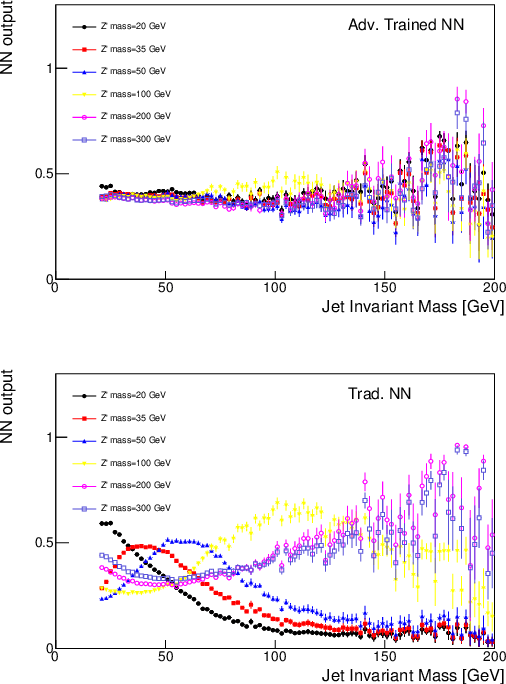
We describe a strategy for constructing a neural network jet substructure tagger which powerfully discriminates boosted decay signals while remaining largely uncorrelated with the jet mass. This reduces the impact of systematic uncertainties in background modeling while enhancing signal purity, resulting in improved discovery significance relative to existing taggers. The network is trained using an adversarial strategy, resulting in a tagger that learns to balance classification accuracy with decorrelation. As a benchmark scenario, we consider the case where large-radius jets originating from a boosted resonance decay are discriminated from a background of nonresonant quark and gluon jets. We show that in the presence of systematic uncertainties on the background rate, our adversarially-trained, decorrelated tagger considerably outperforms a conventionally trained neural network, despite having a slightly worse signal-background separation power. We generalize the adversarial training technique to include a parametric dependence on the signal hypothesis, training a single network that provides optimized, interpolatable decorrelated jet tagging across a continuous range of hypothetical resonance masses, after training on discrete choices of the signal mass.