Interpretability Needs a New Paradigm

Interpretability is the study of explaining models in understandable terms to humans. At present, interpretability is divided into two paradigms: the intrinsic paradigm, which believes that only models designed to be explained can be explained, and the post-hoc paradigm, which believes that black-box models can be explained. At the core of this debate is how each paradigm ensures its explanations are faithful, i.e., true to the model's behavior. This is important, as false but convincing explanations lead to unsupported confidence in artificial intelligence (AI), which can be dangerous. This paper's position is that we should think about new paradigms while staying vigilant regarding faithfulness. First, by examining the history of paradigms in science, we see that paradigms are constantly evolving. Then, by examining the current paradigms, we can understand their underlying beliefs, the value they bring, and their limitations. Finally, this paper presents 3 emerging paradigms for interpretability. The first paradigm designs models such that faithfulness can be easily measured. Another optimizes models such that explanations become faithful. The last paradigm proposes to develop models that produce both a prediction and an explanation.

Are self-explanations from Large Language Models faithful?

Instruction-tuned large language models (LLMs) excel at many tasks, and will even provide explanations for their behavior. Since these models are directly accessible to the public, there is a risk that convincing and wrong explanations can lead to unsupported confidence in LLMs. Therefore, interpretability-faithfulness of self-explanations is an important consideration for AI Safety. Assessing the interpretability-faithfulness of these explanations, termed self-explanations, is challenging as the models are too complex for humans to annotate what is a correct explanation. To address this, we propose employing self-consistency checks as a measure of faithfulness. For example, if an LLM says a set of words is important for making a prediction, then it should not be able to make the same prediction without these words. While self-consistency checks are a common approach to faithfulness, they have not previously been applied to LLM's self-explanations. We apply self-consistency checks to three types of self-explanations: counterfactuals, importance measures, and redactions. Our work demonstrate that faithfulness is both task and model dependent, e.g., for sentiment classification, counterfactual explanations are more faithful for Llama2, importance measures for Mistral, and redaction for Falcon 40B. Finally, our findings are robust to prompt-variations.

Faithfulness Measurable Masked Language Models

A common approach to explain NLP models, is to use importance measures that express which tokens are important for a prediction. Unfortunately, such explanations are often wrong despite being persuasive. Therefore, it is essential to measure their faithfulness. One such metric is if tokens are truly important, then masking them should result in worse model performance. However, token masking introduces out-of-distribution issues and existing solutions are computationally expensive and employ proxy-models. Furthermore, other metrics are very limited in scope. In this work, we propose an inherently faithfulness measurable model that addresses these challenges. This is achieved by using a novel fine-tuning method that incorporates masking, such that masking tokens become in-distribution by design. This differs from existing approaches, which are completely model-agnostic but are inapplicable in practice. We demonstrate the generality of our approach by applying it to various tasks and validate it using statistical in-distribution tests. Additionally, because masking is in-distribution, importance measures which themselves use masking become more faithful, thus our model becomes more explainable.

Evaluating the Faithfulness of Importance Measures in NLP by Recursively Masking Allegedly Important Tokens and Retraining

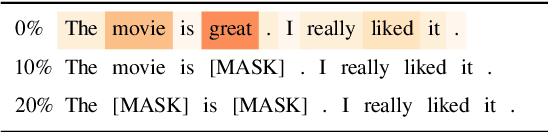
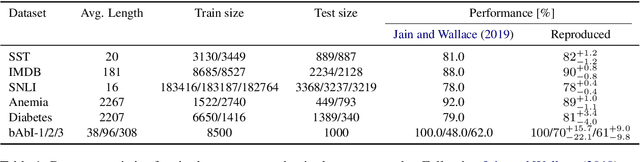
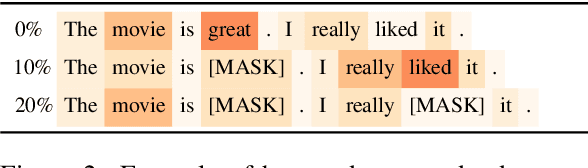
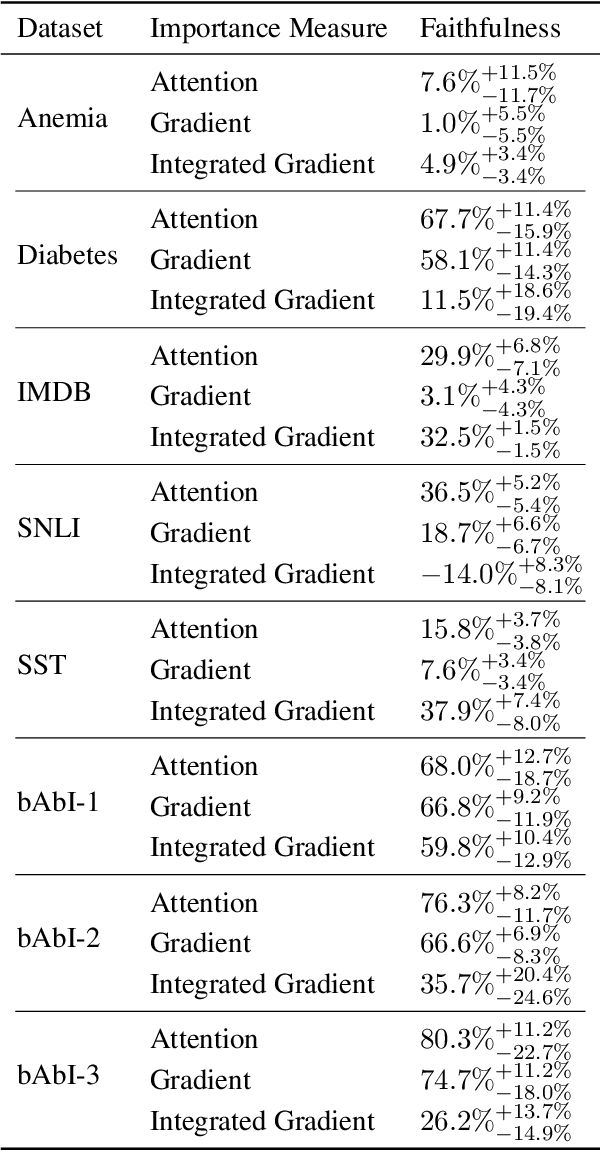
To explain NLP models, many methods inform which inputs tokens are important for a prediction. However, an open question is if these methods accurately reflect the model's logic, a property often called faithfulness. In this work, we adapt and improve a recently proposed faithfulness benchmark from computer vision called ROAR (RemOve And Retrain), by Hooker et al. (2019). We improve ROAR by recursively removing dataset redundancies, which otherwise interfere with ROAR. We adapt and apply ROAR, to popular NLP importance measures, namely attention, gradient, and integrated gradients. Additionally, we use mutual information as an additional baseline. Evaluation is done on a suite of classification tasks often used in the faithfulness of attention literature. Finally, we propose a scalar faithfulness metric, which makes it easy to compare results across papers. We find that, importance measures considered to be unfaithful for computer vision tasks perform favorably for NLP tasks, the faithfulness of an importance measure is task-dependent, and the computational overhead of integrated gradient is rarely justified.

Post-hoc Interpretability for Neural NLP: A Survey

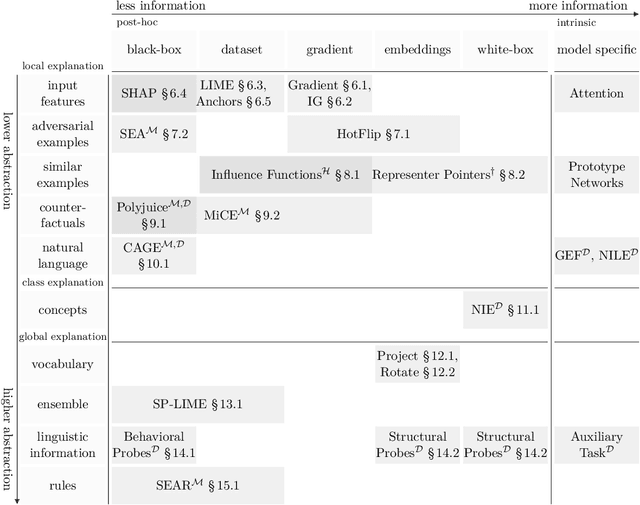
Natural Language Processing (NLP) models have become increasingly more complex and widespread. With recent developments in neural networks, a growing concern is whether it is responsible to use these models. Concerns such as safety and ethics can be partially addressed by providing explanations. Furthermore, when models do fail, providing explanations is paramount for accountability purposes. To this end, interpretability serves to provide these explanations in terms that are understandable to humans. Central to what is understandable is how explanations are communicated. Therefore, this survey provides a categorization of how recent interpretability methods communicate explanations and discusses the methods in depth. Furthermore, the survey focuses on post-hoc methods, which provide explanations after a model is learned and generally model-agnostic. A common concern for this class of methods is whether they accurately reflect the model. Hence, how these post-hoc methods are evaluated is discussed throughout the paper.

Neural Arithmetic Units

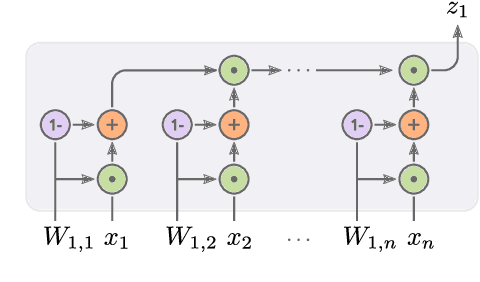
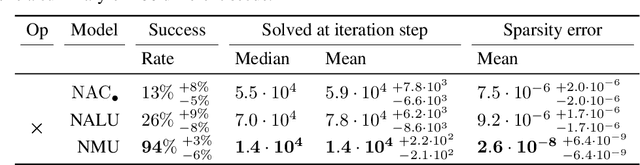
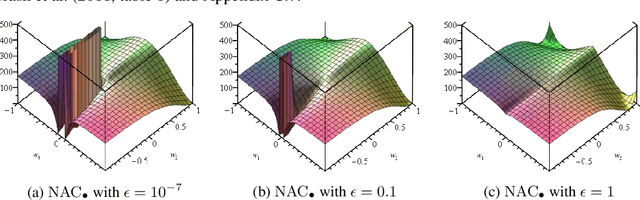
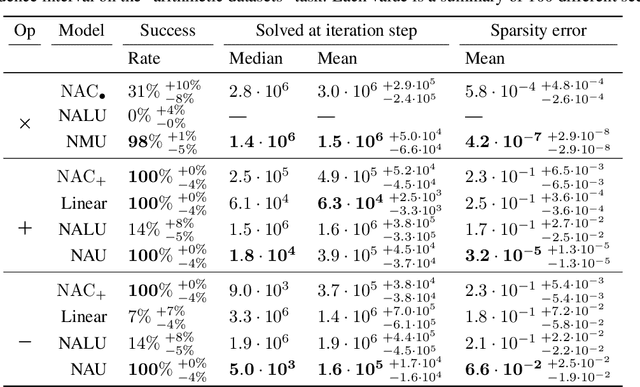
Neural networks can approximate complex functions, but they struggle to perform exact arithmetic operations over real numbers. The lack of inductive bias for arithmetic operations leaves neural networks without the underlying logic necessary to extrapolate on tasks such as addition, subtraction, and multiplication. We present two new neural network components: the Neural Addition Unit (NAU), which can learn exact addition and subtraction; and the Neural Multiplication Unit (NMU) that can multiply subsets of a vector. The NMU is, to our knowledge, the first arithmetic neural network component that can learn to multiply elements from a vector, when the hidden size is large. The two new components draw inspiration from a theoretical analysis of recently proposed arithmetic components. We find that careful initialization, restricting parameter space, and regularizing for sparsity is important when optimizing the NAU and NMU. Our proposed units NAU and NMU, compared with previous neural units, converge more consistently, have fewer parameters, learn faster, can converge for larger hidden sizes, obtain sparse and meaningful weights, and can extrapolate to negative and small values.

Measuring Arithmetic Extrapolation Performance

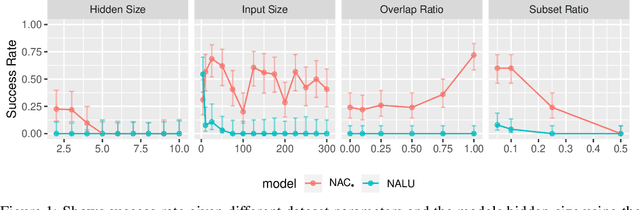
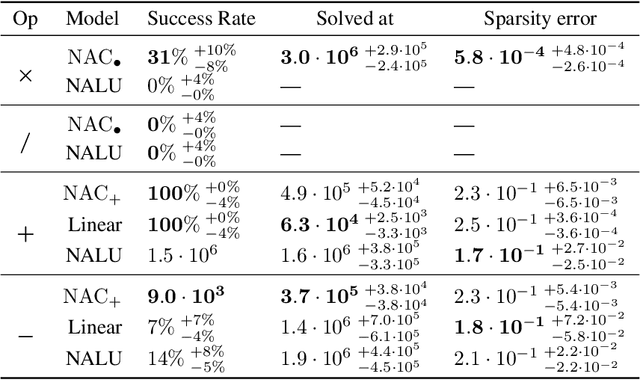
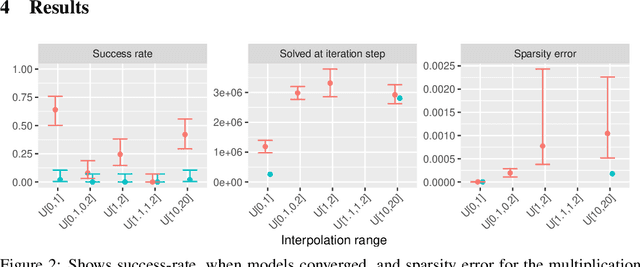
The Neural Arithmetic Logic Unit (NALU) is a neural network layer that can learn exact arithmetic operations between the elements of a hidden state. The goal of NALU is to learn perfect extrapolation, which requires learning the exact underlying logic of an unknown arithmetic problem. Evaluating the performance of the NALU is non-trivial as one arithmetic problem might have many solutions. As a consequence, single-instance MSE has been used to evaluate and compare performance between models. However, it can be hard to interpret what magnitude of MSE represents a correct solution and models sensitivity to initialization. We propose using a success-criterion to measure if and when a model converges. Using a success-criterion we can summarize success-rate over many initialization seeds and calculate confidence intervals. We contribute a generalized version of the previous arithmetic benchmark to measure models sensitivity under different conditions. This is, to our knowledge, the first extensive evaluation with respect to convergence of the NALU and its sub-units. Using a success-criterion to summarize 4800 experiments we find that consistently learning arithmetic extrapolation is challenging, in particular for multiplication.