RIP sensing matrices construction for sparsifying dictionaries with application to MRI imaging

Practical applications of compressed sensing often restrict the choice of its two main ingredients. They may (i) prescribe using particular redundant dictionaries for certain classes of signals to become sparsely represented, or (ii) dictate specific measurement mechanisms which exploit certain physical principles. On the problem of RIP measurement matrix design in compressed sensing with redundant dictionaries, we give a simple construction to derive sensing matrices whose compositions with a prescribed dictionary have a high probability of the RIP in the $k \log(n/k)$ regime. Our construction thus provides recovery guarantees usually only attainable for sensing matrices from random ensembles with sparsifying orthonormal bases. Moreover, we use the dictionary factorization idea that our construction rests on in the application of magnetic resonance imaging, in which also the sensing matrix is prescribed by quantum mechanical principles. We propose a recovery algorithm based on transforming the acquired measurements such that the compressed sensing theory for RIP embeddings can be utilized to recover wavelet coefficients of the target image, and show its performance on examples from the fastMRI dataset.

Unsupervised Statistical Learning for Die Analysis in Ancient Numismatics

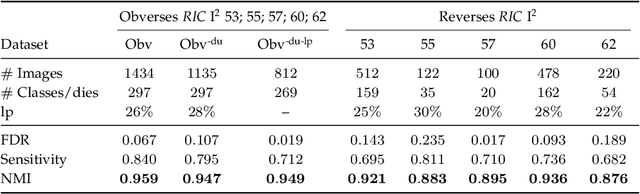
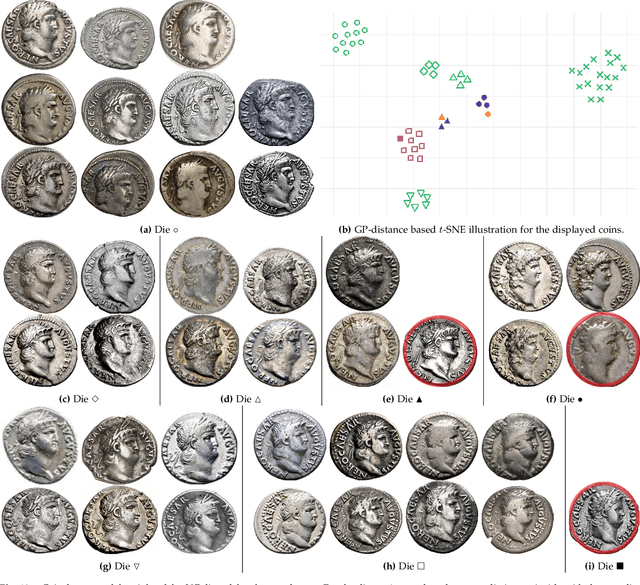
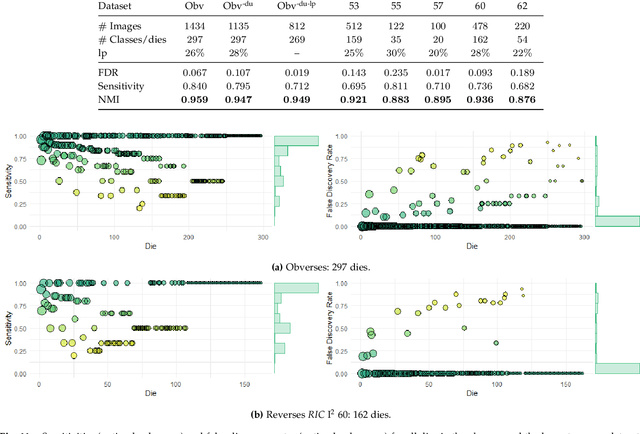
Die analysis is an essential numismatic method, and an important tool of ancient economic history. Yet, manual die studies are too labor-intensive to comprehensively study large coinages such as those of the Roman Empire. We address this problem by proposing a model for unsupervised computational die analysis, which can reduce the time investment necessary for large-scale die studies by several orders of magnitude, in many cases from years to weeks. From a computer vision viewpoint, die studies present a challenging unsupervised clustering problem, because they involve an unknown and large number of highly similar semantic classes of imbalanced sizes. We address these issues through determining dissimilarities between coin faces derived from specifically devised Gaussian process-based keypoint features in a Bayesian distance clustering framework. The efficacy of our method is demonstrated through an analysis of 1135 Roman silver coins struck between 64-66 C.E..

Deep Representation with ReLU Neural Networks

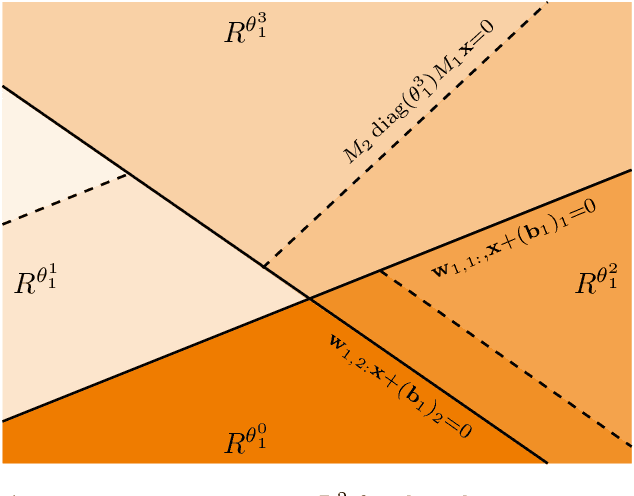
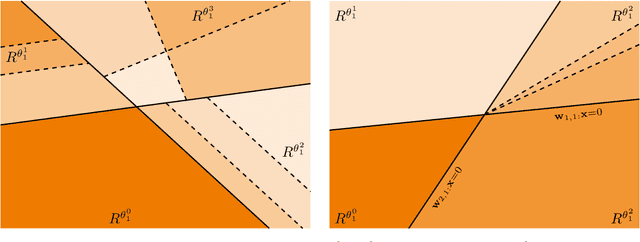
We consider deep feedforward neural networks with rectified linear units from a signal processing perspective. In this view, such representations mark the transition from using a single (data-driven) linear representation to utilizing a large collection of affine linear representations tailored to particular regions of the signal space. This paper provides a precise description of the individual affine linear representations and corresponding domain regions that the (data-driven) neural network associates to each signal of the input space. In particular, we describe atomic decompositions of the representations and, based on estimating their Lipschitz regularity, suggest some conditions that can stabilize learning independent of the network depth. Such an analysis may promote further theoretical insight from both the signal processing and machine learning communities.