A Systematic Framework to Test the Resilience of Three-Fold Redundant Sparse Arrays Against Two Sensor Failures and Some Never-Before Findings

As the field of sparse arrays progressed, numerous array designs have been introduced with a focus on larger apertures and higher degrees of freedom (DOFs), resulting in maximally economic sparse arrays (MESAs) that operate with the least number of sensors required to provide a given aperture while ensuring a hole-free difference coarray (DCA). Consequently, MESAs are least robust to sensor failures and cannot afford the failure of even a single sensor. Multifold redundant sparse arrays (MFRSAs) provide a practical solution to the problem of sensor failures in sparse arrays by making sure that the array contains enough sensor pairs necessary to produce each spatial lag multiple times. Owing to this property, a \b{eta}-fold redundant array can withstand simultaneous failure of at least \b{eta}-1 sensors without losing the hole-free DCA property. Nevertheless, MFRSAs are also prone to hidden dependencies that prevent them from being fully robust. In this work, we present a systematic framework to evaluate the robustness of triple redundant sparse linear arrays (TRSLAs) against all possible two-sensor failures. After detailing the proposed approach, we present the failure analysis of representative TRSLAs available in existing literature. It is found that existing TRSLAs have some hidden vulnerabilities against the failure of some peculiar sensor pairs. Corresponding MATLAB programs and numerical simulations are provided for evaluation and use by the array processing community. The proposed approach has a great archival value as it can evaluate the robustness of any present or future TRSLAs through objective means.

Stochastic Phased Array Performance Indicators for Quality-of-Service-Enhanced Massive MIMO

In this paper, we show that the signal-to-interference-plus-noise ratio (SINR) at a base station (BS) equipped with an arbitrary physical array antenna can be expressed as a function of two fundamental figures-of-merit (FoMs): (I) the instantaneous effective gain (IEG), and (II) the beamforming-channel correlation (BCC). These two FoMs are functions of the array antenna layout, the antenna elements, the propagation channel and the applied signal processing algorithms, and hence they are random variables (RVs) in general. We illustrate that both FoMs provide essential insights for quality-of-service (QoS)-based phased array design by investigating their statistics for BSs applying full-digital (FD) zero forcing (ZF) beamforming. We evaluate various array designs and show that arrays with higher IEGs and a reduced probability of low BCCs can increase the ergodic sum rate and reduce the need for scheduling.

A Supervised Learning Framework for Joint Angle-of-Arrival and Source Number Estimation

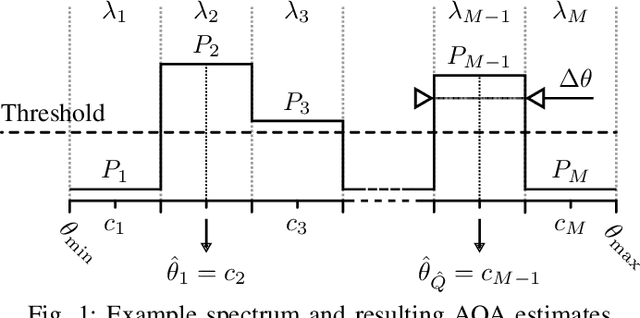
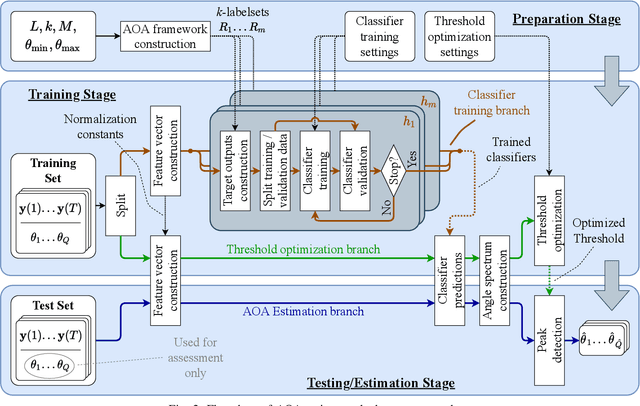
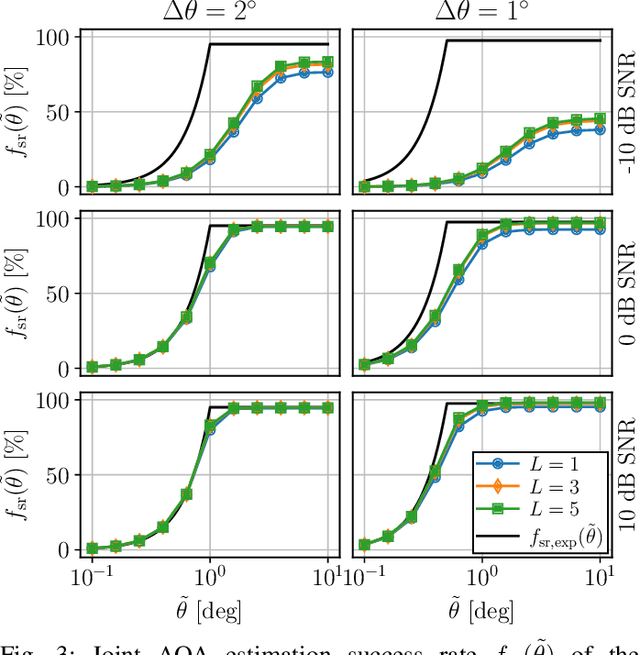
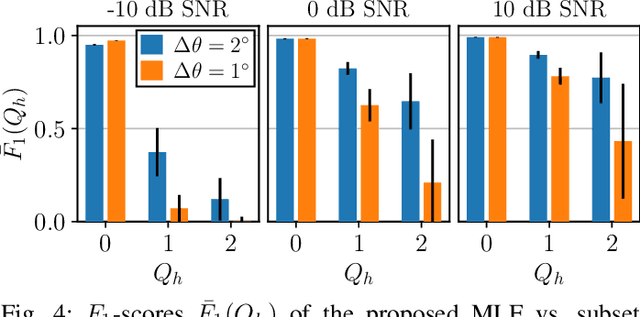
Machine learning is a promising technique for angle-of-arrival (AOA) estimation of waves impinging a sensor array. However, the majority of the methods proposed so far only consider a known, fixed number of impinging waves, i.e., a fixed source number. This paper proposes a machine-learning-based estimator designed for the case when the source number is variable and hence unknown a priori. The proposed estimator comprises a framework of single-label classifiers. Each classifier predicts if waves are present within certain randomly selected segments of the array's field of view (FOV), resulting from discretising the FOV with a certain (FOV) resolution. The classifiers' predictions are combined into a probabilistic angle spectrum, whereupon the source number and the AOAs are estimated jointly by applying a probability threshold whose optimal level is learned from data. The estimator's performance is assessed using a new performance metric: the joint AOA estimation success rate. Numerical simulations show that for low SNR (-10 dB), a low FOV resolution (2$^\circ$) yields a higher success rate than a high resolution (1$^\circ$), whereas the opposite applies for mid (0 dB) and high (10 dB) SNRs. In nearly all simulations, except one at low SNR and a high FOV resolution, the proposed estimator outperforms the MUSIC algorithm if the maximum allowed AOA estimation error is approximately equal to (or larger than) the FOV resolution.