Hybrid quantum-classical algorithm for near-optimal planning in POMDPs

Reinforcement learning (RL) provides a principled framework for decision-making in partially observable environments, which can be modeled as Markov decision processes and compactly represented through dynamic decision Bayesian networks. Recent advances demonstrate that inference on sparse Bayesian networks can be accelerated using quantum rejection sampling combined with amplitude amplification, leading to a computational speedup in estimating acceptance probabilities.\\ Building on this result, we introduce Quantum Bayesian Reinforcement Learning (QBRL), a hybrid quantum-classical look-ahead algorithm for model-based RL in partially observable environments. We present a rigorous, oracle-free time complexity analysis under fault-tolerant assumptions for the quantum device. Unlike standard treatments that assume a black-box oracle, we explicitly specify the inference process, allowing our bounds to more accurately reflect the true computational cost. We show that, for environments whose dynamics form a sparse Bayesian network, horizon-based near-optimal planning can be achieved sub-quadratically faster through quantum-enhanced belief updates. Furthermore, we present numerical experiments benchmarking QBRL against its classical counterpart on simple yet illustrative decision-making tasks. Our results offer a detailed analysis of how the quantum computational advantage translates into decision-making performance, highlighting that the magnitude of the advantage can vary significantly across different deployment settings.

Trainability issues in quantum policy gradients

This research explores the trainability of Parameterized Quantum circuit-based policies in Reinforcement Learning, an area that has recently seen a surge in empirical exploration. While some studies suggest improved sample complexity using quantum gradient estimation, the efficient trainability of these policies remains an open question. Our findings reveal significant challenges, including standard Barren Plateaus with exponentially small gradients and gradient explosion. These phenomena depend on the type of basis-state partitioning and mapping these partitions onto actions. For a polynomial number of actions, a trainable window can be ensured with a polynomial number of measurements if a contiguous-like partitioning of basis-states is employed. These results are empirically validated in a multi-armed bandit environment.

VQC-Based Reinforcement Learning with Data Re-uploading: Performance and Trainability

Reinforcement Learning (RL) consists of designing agents that make intelligent decisions without human supervision. When used alongside function approximators such as Neural Networks (NNs), RL is capable of solving extremely complex problems. Deep Q-Learning, a RL algorithm that uses Deep NNs, achieved super-human performance in some specific tasks. Nonetheless, it is also possible to use Variational Quantum Circuits (VQCs) as function approximators in RL algorithms. This work empirically studies the performance and trainability of such VQC-based Deep Q-Learning models in classic control benchmark environments. More specifically, we research how data re-uploading affects both these metrics. We show that the magnitude and the variance of the gradients of these models remain substantial throughout training due to the moving targets of Deep Q-Learning. Moreover, we empirically show that increasing the number of qubits does not lead to an exponential vanishing behavior of the magnitude and variance of the gradients for a PQC approximating a 2-design, unlike what was expected due to the Barren Plateau Phenomenon. This hints at the possibility of VQCs being specially adequate for being used as function approximators in such a context.

On Quantum Natural Policy Gradients

This research delves into the role of the quantum Fisher Information Matrix (FIM) in enhancing the performance of Parameterized Quantum Circuit (PQC)-based reinforcement learning agents. While previous studies have highlighted the effectiveness of PQC-based policies preconditioned with the quantum FIM in contextual bandits, its impact in broader reinforcement learning contexts, such as Markov Decision Processes, is less clear. Through a detailed analysis of L\"owner inequalities between quantum and classical FIMs, this study uncovers the nuanced distinctions and implications of using each type of FIM. Our results indicate that a PQC-based agent using the quantum FIM without additional insights typically incurs a larger approximation error and does not guarantee improved performance compared to the classical FIM. Empirical evaluations in classic control benchmarks suggest even though quantum FIM preconditioning outperforms standard gradient ascent, in general it is not superior to classical FIM preconditioning.

Variational Quantum Policy Gradients with an Application to Quantum Control

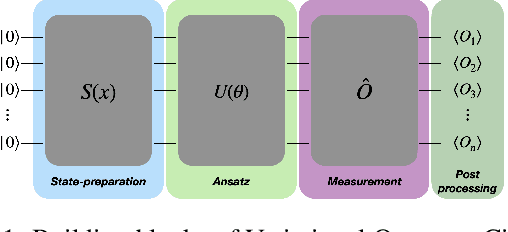
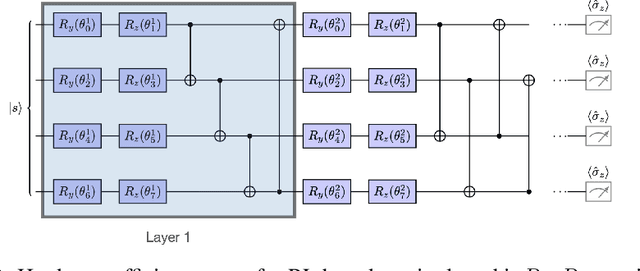
Quantum Machine Learning models are composed by Variational Quantum Circuits (VQCs) in a very natural way. There are already some empirical results proving that such models provide an advantage in supervised/unsupervised learning tasks. However, when applied to Reinforcement Learning (RL), less is known. In this work, we consider Policy Gradients using a hardware-efficient ansatz. We prove that the complexity of obtaining an {\epsilon}-approximation of the gradient using quantum hardware scales only logarithmically with the number of parameters, considering the number of quantum circuits executions. We test the performance of such models in benchmarking environments and verify empirically that such quantum models outperform typical classical neural networks used in those environments, using a fraction of the number of parameters. Moreover, we propose the utilization of the Fisher Information spectrum to show that the quantum model is less prone to barren plateaus than its classical counterpart. As a different use case, we consider the application of such variational quantum models to the problem of quantum control and show its feasibility in the quantum-quantum domain.