Conditional Optimal Transport on Function Spaces

We present a systematic study of conditional triangular transport maps in function spaces from the perspective of optimal transportation and with a view towards amortized Bayesian inference. More specifically, we develop a theory of constrained optimal transport problems that describe block-triangular Monge maps that characterize conditional measures along with their Kantorovich relaxations. This generalizes the theory of optimal triangular transport to separable infinite-dimensional function spaces with general cost functions. We further tailor our results to the case of Bayesian inference problems and obtain regularity estimates on the conditioning maps from the prior to the posterior. Finally, we present numerical experiments that demonstrate the computational applicability of our theoretical results for amortized and likelihood-free inference of functional parameters.

Optimal Transport-based Nonlinear Filtering in High-dimensional Settings

This paper addresses the problem of nonlinear filtering, i.e., computing the conditional distribution of the state of a stochastic dynamical system given a history of noisy partial observations. The primary focus is on scenarios involving degenerate likelihoods or high-dimensional states, where traditional sequential importance resampling (SIR) particle filters face the weight degeneracy issue. Our proposed method builds on an optimal transport interpretation of nonlinear filtering, leading to a simulation-based and likelihood-free algorithm that estimates the Brenier optimal transport map from the current distribution of the state to the distribution at the next time step. Our formulation allows us to harness the approximation power of neural networks to model complex and multi-modal distributions and employ stochastic optimization algorithms to enhance scalability. Extensive numerical experiments are presented that compare our method to the SIR particle filter and the ensemble Kalman filter, demonstrating the superior performance of our method in terms of sample efficiency, high-dimensional scalability, and the ability to capture complex and multi-modal distributions.

Duality-Based Stochastic Policy Optimization for Estimation with Unknown Noise Covariances

Duality of control and estimation allows mapping recent advances in data-guided control to the estimation setup. This paper formalizes and utilizes such a mapping by considering learning the optimal (steady-state) Kalman gain when process and measurement noise statistics are unknown. Specifically, building on the duality between synthesizing optimal control and estimation gains, the filter design problem is formalized as direct policy learning; subsequently, a Stochastic Gradient Descent (SGD) approach is adopted to learn the optimal filter gain. In this direction, control and estimation duality is also used to extend existing theoretical results for direct policy updates for Linear Quadratic Regulator (LQR) to establish convergence of the proposed algorithm-while addressing subtle differences between the two synthesis problems. The results are illustrated via several numerical examples.

An Optimal Transport Formulation of Bayes' Law for Nonlinear Filtering Algorithms

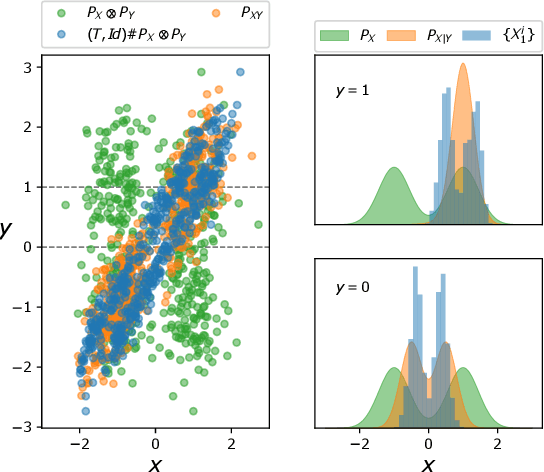
This paper presents a variational representation of the Bayes' law using optimal transportation theory. The variational representation is in terms of the optimal transportation between the joint distribution of the (state, observation) and their independent coupling. By imposing certain structure on the transport map, the solution to the variational problem is used to construct a Brenier-type map that transports the prior distribution to the posterior distribution for any value of the observation signal. The new formulation is used to derive the optimal transport form of the Ensemble Kalman filter (EnKF) for the discrete-time filtering problem and propose a novel extension of EnKF to the non-Gaussian setting utilizing input convex neural networks. Finally, the proposed methodology is used to derive the optimal transport form of the feedback particle filler (FPF) in the continuous-time limit, which constitutes its first variational construction without explicitly using the nonlinear filtering equation or Bayes' law.

Variational Wasserstein gradient flow

The gradient flow of a function over the space of probability densities with respect to the Wasserstein metric often exhibits nice properties and has been utilized in several machine learning applications. The standard approach to compute the Wasserstein gradient flow is the finite difference which discretizes the underlying space over a grid, and is not scalable. In this work, we propose a scalable proximal gradient type algorithm for Wasserstein gradient flow. The key of our method is a variational formulation of the objective function, which makes it possible to realize the JKO proximal map through a primal-dual optimization. This primal-dual problem can be efficiently solved by alternatively updating the parameters in the inner and outer loops. Our framework covers all the classical Wasserstein gradient flows including the heat equation and the porous medium equation. We demonstrate the performance and scalability of our algorithm with several numerical examples.

Deep FPF: Gain function approximation in high-dimensional setting

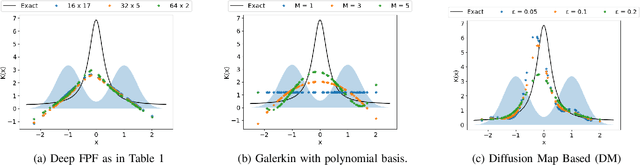
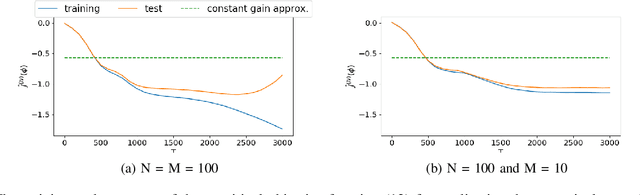
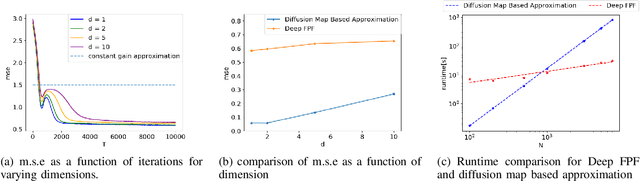
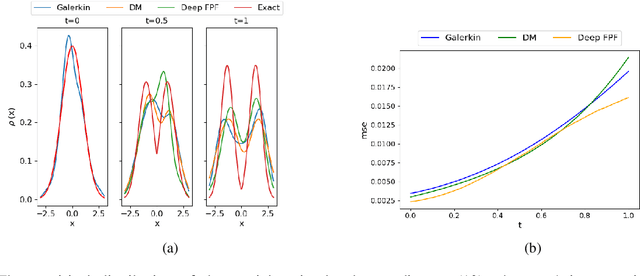
In this paper, we present a novel approach to approximate the gain function of the feedback particle filter (FPF). The exact gain function is the solution of a Poisson equation involving a probability-weighted Laplacian. The numerical problem is to approximate the exact gain function using only finitely many particles sampled from the probability distribution. Inspired by the recent success of the deep learning methods, we represent the gain function as a gradient of the output of a neural network. Thereupon considering a certain variational formulation of the Poisson equation, an optimization problem is posed for learning the weights of the neural network. A stochastic gradient algorithm is described for this purpose. The proposed approach has two significant properties/advantages: (i) The stochastic optimization algorithm allows one to process, in parallel, only a batch of samples (particles) ensuring good scaling properties with the number of particles; (ii) The remarkable representation power of neural networks means that the algorithm is potentially applicable and useful to solve high-dimensional problems. We numerically establish these two properties and provide extensive comparison to the existing approaches.

Scalable Computations of Wasserstein Barycenter via Input Convex Neural Networks

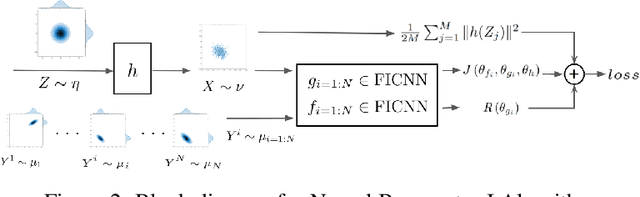
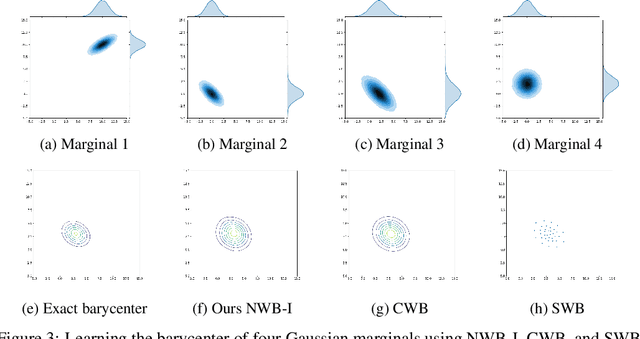
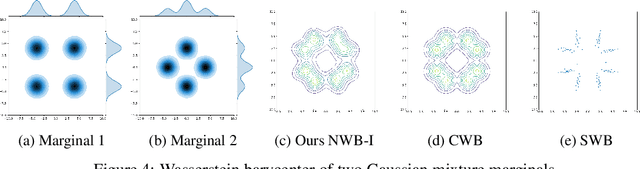
Wasserstein Barycenter is a principled approach to represent the weighted mean of a given set of probability distributions, utilizing the geometry induced by optimal transport. In this work, we present a novel scalable algorithm to approximate the Wasserstein Barycenters aiming at high-dimensional applications in machine learning. Our proposed algorithm is based on the Kantorovich dual formulation of the 2-Wasserstein distance as well as a recent neural network architecture, input convex neural network, that is known to parametrize convex functions. The distinguishing features of our method are: i) it only requires samples from the marginal distributions; ii) unlike the existing semi-discrete approaches, it represents the Barycenter with a generative model; iii) it allows to compute the barycenter with arbitrary weights after one training session. We demonstrate the efficacy of our algorithm by comparing it with the state-of-art methods in multiple experiments.

An Optimal Transport Formulation of the Ensemble Kalman Filter

Controlled interacting particle systems such as the ensemble Kalman filter (EnKF) and the feedback particle filter (FPF) are numerical algorithms to approximate the solution of the nonlinear filtering problem in continuous time. The distinguishing feature of these algorithms is that the Bayesian update step is implemented using a feedback control law. It has been noted in the literature that the control law is not unique. This is the main problem addressed in this paper. To obtain a unique control law, the filtering problem is formulated here as an optimal transportation problem. An explicit formula for the (mean-field type) optimal control law is derived in the linear Gaussian setting. Comparisons are made with the control laws for different types of EnKF algorithms described in the literature. Via empirical approximation of the mean-field control law, a finite-$N$ controlled interacting particle algorithm is obtained. For this algorithm, the equations for empirical mean and covariance are derived and shown to be identical to the Kalman filter. This allows strong conclusions on convergence and error properties based on the classical filter stability theory for the Kalman filter. It is shown that, under certain technical conditions, the mean squared error (m.s.e.) converges to zero even with a finite number of particles. A detailed propagation of chaos analysis is carried out for the finite-$N$ algorithm. The analysis is used to prove weak convergence of the empirical distribution as $N\rightarrow\infty$. For a certain simplified filtering problem, analytical comparison of the m.s.e. with the importance sampling-based algorithms is described. The analysis helps explain the favorable scaling properties of the control-based algorithms reported in several numerical studies in recent literature.

Optimal transport mapping via input convex neural networks

In this paper, we present a novel and principled approach to learn the optimal transport between two distributions, from samples. Guided by the optimal transport theory, we learn the optimal Kantorovich potential which induces the optimal transport map. This involves learning two convex functions, by solving a novel minimax optimization. Building upon recent advances in the field of input convex neural networks, we propose a new framework where the gradient of one convex function represents the optimal transport mapping. Numerical experiments confirm that we learn the optimal transport mapping. This approach ensures that the transport mapping we find is optimal independent of how we initialize the neural networks. Further, target distributions from a discontinuous support can be easily captured, as gradient of a convex function naturally models a {\em discontinuous} transport mapping.

2-Wasserstein Approximation via Restricted Convex Potentials with Application to Improved Training for GANs

We provide a framework to approximate the 2-Wasserstein distance and the optimal transport map, amenable to efficient training as well as statistical and geometric analysis. With the quadratic cost and considering the Kantorovich dual form of the optimal transportation problem, the Brenier theorem states that the optimal potential function is convex and the optimal transport map is the gradient of the optimal potential function. Using this geometric structure, we restrict the optimization problem to different parametrized classes of convex functions and pay special attention to the class of input-convex neural networks. We analyze the statistical generalization and the discriminative power of the resulting approximate metric, and we prove a restricted moment-matching property for the approximate optimal map. Finally, we discuss a numerical algorithm to solve the restricted optimization problem and provide numerical experiments to illustrate and compare the proposed approach with the established regularization-based approaches. We further discuss practical implications of our proposal in a modular and interpretable design for GANs which connects the generator training with discriminator computations to allow for learning an overall composite generator.