Biharmonic Distance of Graphs and its Higher-Order Variants: Theoretical Properties with Applications to Centrality and Clustering

Effective resistance is a distance between vertices of a graph that is both theoretically interesting and useful in applications. We study a variant of effective resistance called the biharmonic distance. While the effective resistance measures how well-connected two vertices are, we prove several theoretical results supporting the idea that the biharmonic distance measures how important an edge is to the global topology of the graph. Our theoretical results connect the biharmonic distance to well-known measures of connectivity of a graph like its total resistance and sparsity. Based on these results, we introduce two clustering algorithms using the biharmonic distance. Finally, we introduce a further generalization of the biharmonic distance that we call the $k$-harmonic distance. We empirically study the utility of biharmonic and $k$-harmonic distance for edge centrality and graph clustering.

Comparing Graph Transformers via Positional Encodings

The distinguishing power of graph transformers is closely tied to the choice of positional encoding: features used to augment the base transformer with information about the graph. There are two primary types of positional encoding: absolute positional encodings (APEs) and relative positional encodings (RPEs). APEs assign features to each node and are given as input to the transformer. RPEs instead assign a feature to each pair of nodes, e.g., graph distance, and are used to augment the attention block. A priori, it is unclear which method is better for maximizing the power of the resulting graph transformer. In this paper, we aim to understand the relationship between these different types of positional encodings. Interestingly, we show that graph transformers using APEs and RPEs are equivalent in terms of distinguishing power. In particular, we demonstrate how to interchange APEs and RPEs while maintaining their distinguishing power in terms of graph transformers. Based on our theoretical results, we provide a study on several APEs and RPEs (including the resistance distance and the recently introduced stable and expressive positional encoding (SPE)) and compare their distinguishing power in terms of transformers. We believe our work will help navigate the huge number of choices of positional encoding and will provide guidance on the future design of positional encodings for graph transformers.

Understanding Oversquashing in GNNs through the Lens of Effective Resistance

Message passing graph neural networks are popular learning architectures for graph-structured data. However, it can be challenging for them to capture long range interactions in graphs. One of the potential reasons is the so-called oversquashing problem, first termed in [Alon and Yahav, 2020], that has recently received significant attention. In this paper, we analyze the oversquashing problem through the lens of effective resistance between nodes in the input graphs. The concept of effective resistance intuitively captures the "strength" of connection between two nodes by paths in the graph, and has a rich literature connecting spectral graph theory and circuit networks theory. We propose the use the concept of total effective resistance as a measure to quantify the total amount of oversquashing in a graph, and provide theoretical justification of its use. We further develop algorithms to identify edges to be added to an input graph so as to minimize the total effective resistance, thereby alleviating the oversquashing problem when using GNNs. We provide empirical evidence of the effectiveness of our total effective resistance based rewiring strategies.

On Cyclic Solutions to the Min-Max Latency Multi-Robot Patrolling Problem

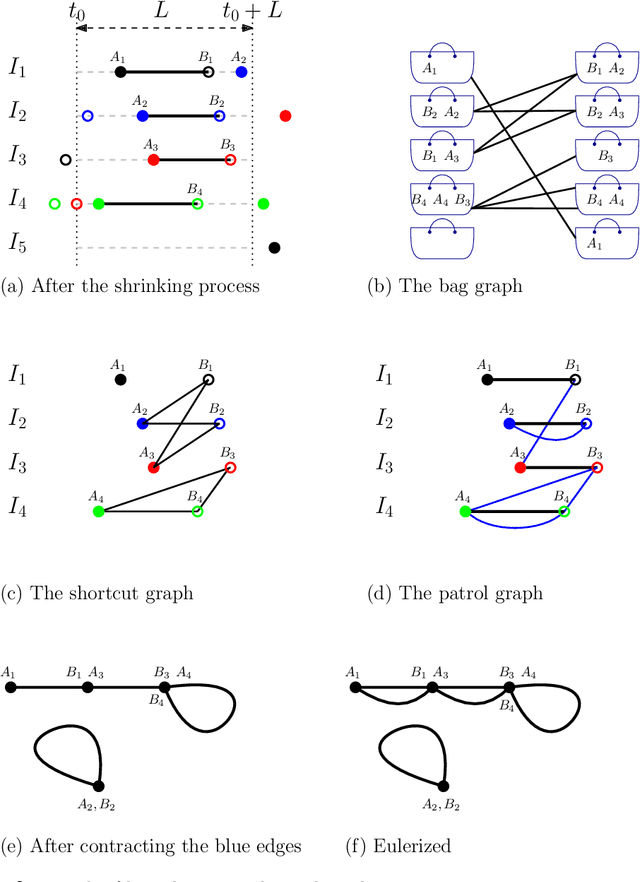
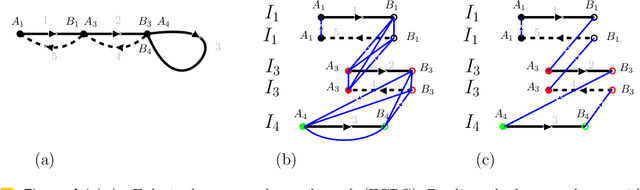
We consider the following surveillance problem: Given a set $P$ of $n$ sites in a metric space and a set of $k$ robots with the same maximum speed, compute a patrol schedule of minimum latency for the robots. Here a patrol schedule specifies for each robot an infinite sequence of sites to visit (in the given order) and the latency $L$ of a schedule is the maximum latency of any site, where the latency of a site $s$ is the supremum of the lengths of the time intervals between consecutive visits to $s$. When $k=1$ the problem is equivalent to the travelling salesman problem (TSP) and thus it is NP-hard. We have two main results. We consider cyclic solutions in which the set of sites must be partitioned into $\ell$ groups, for some~$\ell \leq k$, and each group is assigned a subset of the robots that move along the travelling salesman tour of the group at equal distance from each other. Our first main result is that approximating the optimal latency of the class of cyclic solutions can be reduced to approximating the optimal travelling salesman tour on some input, with only a $1+\varepsilon$ factor loss in the approximation factor and an $O\left(\left( k/\varepsilon \right)^k\right)$ factor loss in the runtime, for any $\varepsilon >0$. Our second main result shows that an optimal cyclic solution is a $2(1-1/k)$-approximation of the overall optimal solution. Note that for $k=2$ this implies that an optimal cyclic solution is optimal overall. The results have a number of consequences. For the Euclidean version of the problem, for instance, combining our results with known results on Euclidean TSP, yields a PTAS for approximating an optimal cyclic solution, and it yields a $(2(1-1/k)+\varepsilon)$-approximation of the optimal unrestricted solution. If the conjecture mentioned above is true, then our algorithm is actually a PTAS for the general problem in the Euclidean setting.

Approximation Algorithms for Multi-Robot Patrol-Scheduling with Min-Max Latency

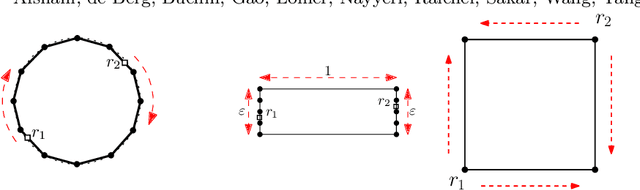
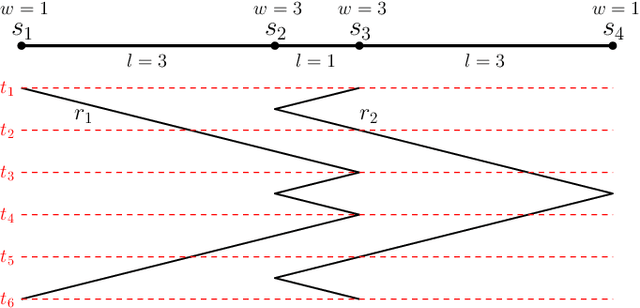
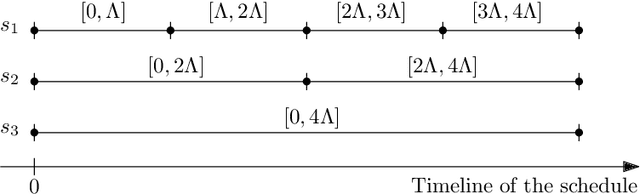
We consider the problem of finding patrol schedules for $k$ robots to visit a given set of $n$ sites in a metric space. Each robot has the same maximum speed and the goal is to minimize the weighted maximum latency of any site, where the latency of a site is defined as the maximum time duration between consecutive visits of that site. The problem is NP-hard, as it has the traveling salesman problem as a special case (when $k=1$ and all sites have the same weight). We present a polynomial-time algorithm with an approximation factor of $O(k^2 \log \frac{w_{\max}}{w_{\min}})$ to the optimal solution, where $w_{\max}$ and $w_{\min}$ are the maximum and minimum weight of the sites respectively. Further, we consider the special case where the sites are in 1D. When all sites have the same weight, we present a polynomial-time algorithm to solve the problem exactly. If the sites may have different weights, we present a $12$-approximate solution, which runs in polynomial time when the number of robots, $k$, is a constant.