A composable autoencoder-based iterative algorithm for accelerating numerical simulations

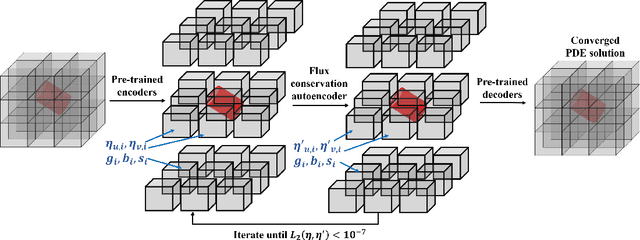
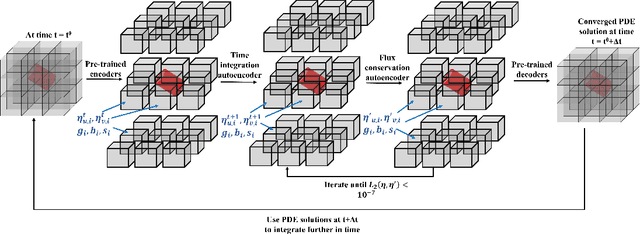
Numerical simulations for engineering applications solve partial differential equations (PDE) to model various physical processes. Traditional PDE solvers are very accurate but computationally costly. On the other hand, Machine Learning (ML) methods offer a significant computational speedup but face challenges with accuracy and generalization to different PDE conditions, such as geometry, boundary conditions, initial conditions and PDE source terms. In this work, we propose a novel ML-based approach, CoAE-MLSim (Composable AutoEncoder Machine Learning Simulation), which is an unsupervised, lower-dimensional, local method, that is motivated from key ideas used in commercial PDE solvers. This allows our approach to learn better with relatively fewer samples of PDE solutions. The proposed ML-approach is compared against commercial solvers for better benchmarks as well as latest ML-approaches for solving PDEs. It is tested for a variety of complex engineering cases to demonstrate its computational speed, accuracy, scalability, and generalization across different PDE conditions. The results show that our approach captures physics accurately across all metrics of comparison (including measures such as results on section cuts and lines).

OVERT: An Algorithm for Safety Verification of Neural Network Control Policies for Nonlinear Systems

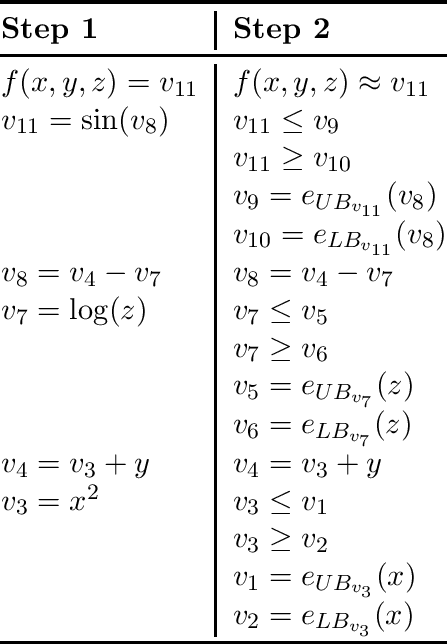
Deep learning methods can be used to produce control policies, but certifying their safety is challenging. The resulting networks are nonlinear and often very large. In response to this challenge, we present OVERT: a sound algorithm for safety verification of nonlinear discrete-time closed loop dynamical systems with neural network control policies. The novelty of OVERT lies in combining ideas from the classical formal methods literature with ideas from the newer neural network verification literature. The central concept of OVERT is to abstract nonlinear functions with a set of optimally tight piecewise linear bounds. Such piecewise linear bounds are designed for seamless integration into ReLU neural network verification tools. OVERT can be used to prove bounded-time safety properties by either computing reachable sets or solving feasibility queries directly. We demonstrate various examples of safety verification for several classical benchmark examples. OVERT compares favorably to existing methods both in computation time and in tightness of the reachable set.

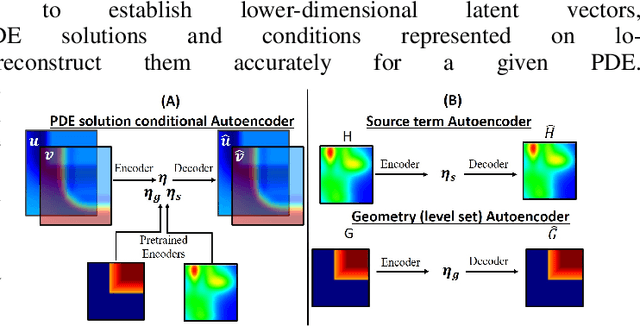
Geometry encoding for numerical simulations

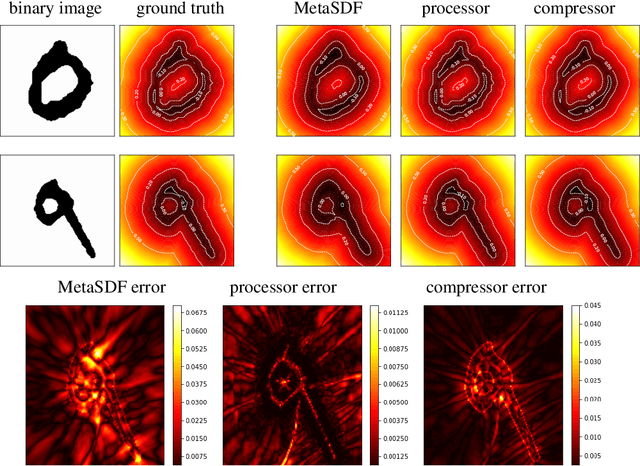
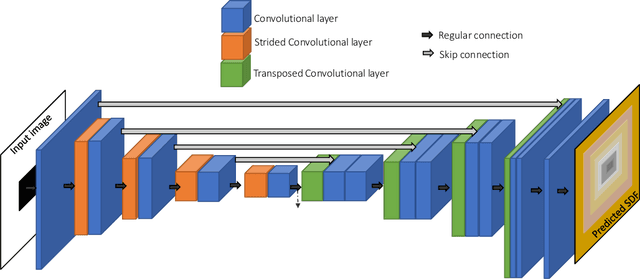
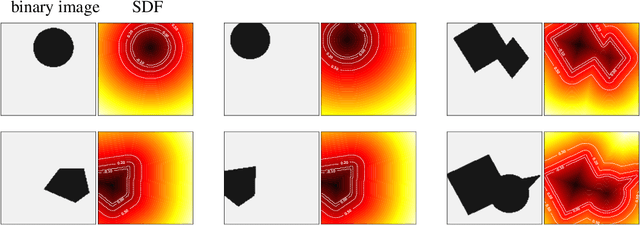
We present a notion of geometry encoding suitable for machine learning-based numerical simulation. In particular, we delineate how this notion of encoding is different than other encoding algorithms commonly used in other disciplines such as computer vision and computer graphics. We also present a model comprised of multiple neural networks including a processor, a compressor and an evaluator.These parts each satisfy a particular requirement of our encoding. We compare our encoding model with the analogous models in the literature

A Latent space solver for PDE generalization

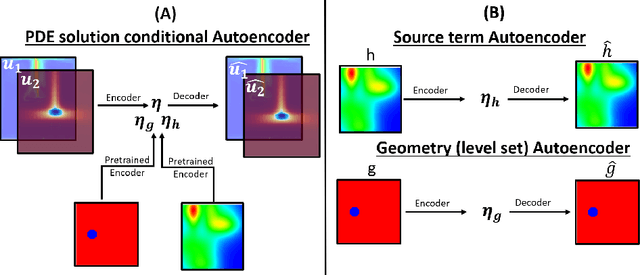
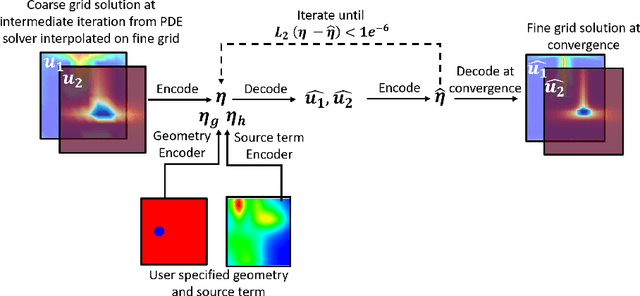
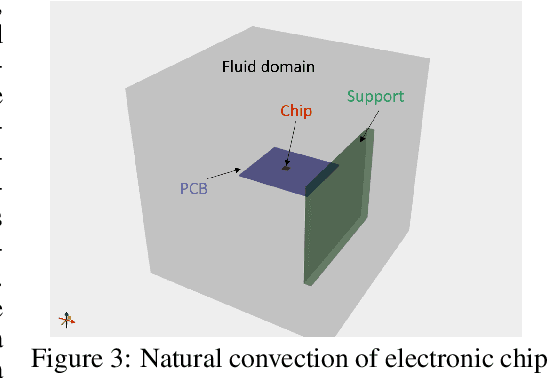
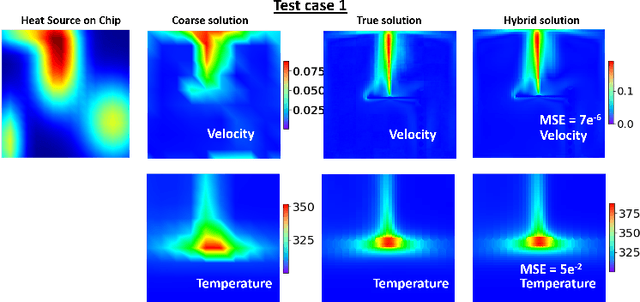
In this work we propose a hybrid solver to solve partial differential equation (PDE)s in the latent space. The solver uses an iterative inferencing strategy combined with solution initialization to improve generalization of PDE solutions. The solver is tested on an engineering case and the results show that it can generalize well to several PDE conditions.

Preference-based Learning of Reward Function Features

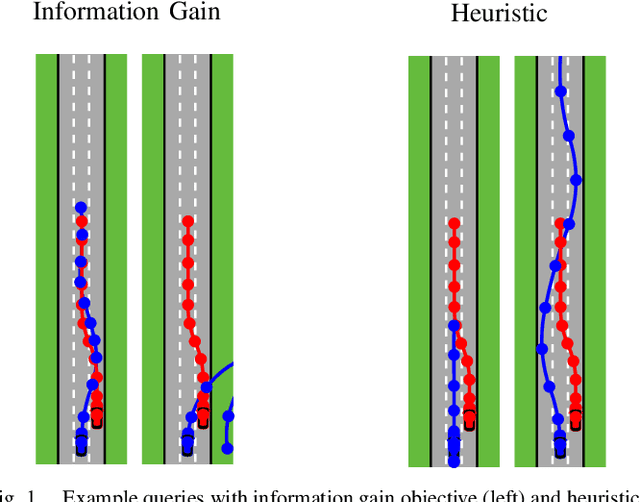
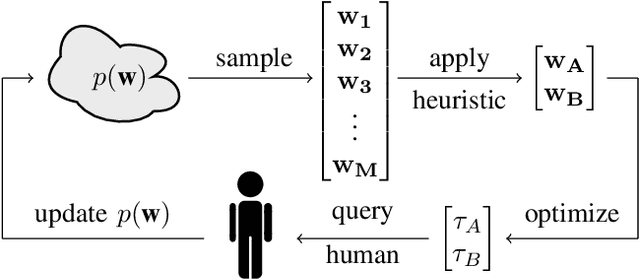
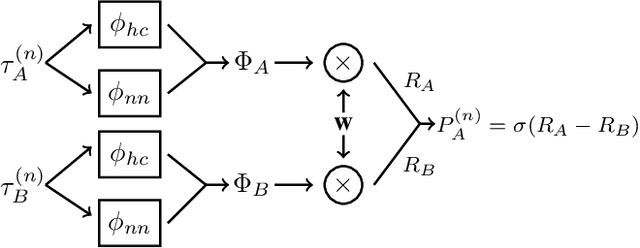
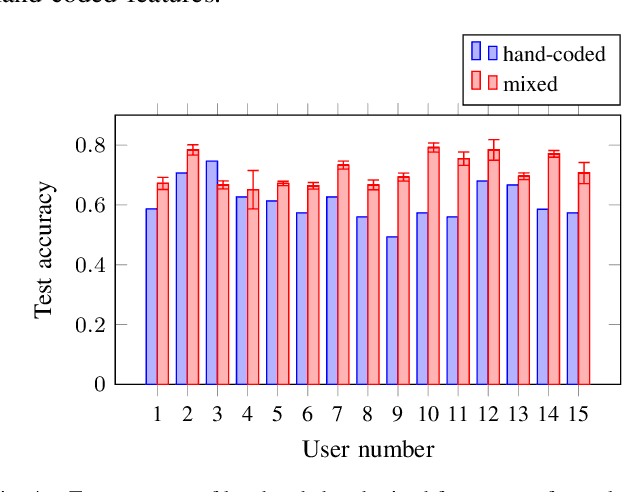
Preference-based learning of reward functions, where the reward function is learned using comparison data, has been well studied for complex robotic tasks such as autonomous driving. Existing algorithms have focused on learning reward functions that are linear in a set of trajectory features. The features are typically hand-coded, and preference-based learning is used to determine a particular user's relative weighting for each feature. Designing a representative set of features to encode reward is challenging and can result in inaccurate models that fail to model the users' preferences or perform the task properly. In this paper, we present a method to learn both the relative weighting among features as well as additional features that help encode a user's reward function. The additional features are modeled as a neural network that is trained on the data from pairwise comparison queries. We apply our methods to a driving scenario used in previous work and compare the predictive power of our method to that of only hand-coded features. We perform additional analysis to interpret the learned features and examine the optimal trajectories. Our results show that adding an additional learned feature to the reward model enhances both its predictive power and expressiveness, producing unique results for each user.