A Characterization of Online Multiclass Learnability

We consider the problem of online multiclass learning when the number of labels is unbounded. We show that the Multiclass Littlestone dimension, first introduced in \cite{DanielyERMprinciple}, continues to characterize online learnability in this setting. Our result complements the recent work by \cite{Brukhimetal2022} who give a characterization of batch multiclass learnability when the label space is unbounded.

Quantum Learning Theory Beyond Batch Binary Classification

Arunachalam and de Wolf (2018) showed that the sample complexity of quantum batch learning of boolean functions, in the realizable and agnostic settings, has the same form and order as the corresponding classical sample complexities. In this paper, we extend this, ostensibly surprising, message to batch multiclass learning, online boolean learning, and online multiclass learning. For our online learning results, we first consider an adaptive adversary variant of the classical model of Dawid and Tewari (2022). Then, we introduce the first (to the best of our knowledge) model of online learning with quantum examples.

An Asymptotically Optimal Algorithm for the One-Dimensional Convex Hull Feasibility Problem

This work studies the pure-exploration setting for the convex hull feasibility (CHF) problem where one aims to efficiently and accurately determine if a given point lies in the convex hull of means of a finite set of distributions. We give a complete characterization of the sample complexity of the CHF problem in the one-dimensional setting. We present the first asymptotically optimal algorithm called Thompson-CHF, whose modular design consists of a stopping rule and a sampling rule. In addition, we provide an extension of the algorithm that generalizes several important problems in the multi-armed bandit literature. Finally, we further investigate the Gaussian bandit case with unknown variances and address how the Thompson-CHF algorithm can be adjusted to be asymptotically optimal in this setting.

Tale of two c(omplex)ities

For decades, best subset selection (BSS) has eluded statisticians mainly due to its computational bottleneck. However, until recently, modern computational breakthroughs have rekindled theoretical interest in BSS and have led to new findings. Recently, Guo et al. (2020) showed that the model selection performance of BSS is governed by a margin quantity that is robust to the design dependence, unlike modern methods such as LASSO, SCAD, MCP, etc. Motivated by their theoretical results, in this paper, we also study the variable selection properties of best subset selection for high-dimensional sparse linear regression setup. We show that apart from the identifiability margin, the following two complexity measures play a fundamental role in characterizing the margin condition for model consistency: (a) complexity of residualized features, (b) complexity of spurious projections. In particular, we establish a simple margin condition that only depends only on the identifiability margin quantity and the dominating one of the two complexity measures. Furthermore, we show that a similar margin condition depending on similar margin quantity and complexity measures is also necessary for model consistency of BSS. For a broader understanding of the complexity measures, we also consider some simple illustrative examples to demonstrate the variation in the complexity measures which broadens our theoretical understanding of the model selection performance of BSS under different correlation structures.

A Characterization of Multilabel Learnability

We consider the problem of multilabel classification and investigate learnability in batch and online settings. In both settings, we show that a multilabel function class is learnable if and only if each single-label restriction of the function class is learnable. As extensions, we also study multioutput regression in the batch setting and bandit feedback in the online setting. For the former, we characterize learnability w.r.t. $L_p$ losses. For the latter, we show a similar characterization as in the full-feedback setting.

Offline Policy Evaluation and Optimization under Confounding

With a few exceptions, work in offline reinforcement learning (RL) has so far assumed that there is no confounding. In a classical regression setting, confounders introduce omitted variable bias and inhibit the identification of causal effects. In offline RL, they prevent the identification of a policy's value, and therefore make it impossible to perform policy improvement. Using conventional methods in offline RL in the presence of confounding can therefore not only lead to poor decisions and poor policies, but can also have disastrous effects in applications such as healthcare and education. We provide approaches for both off-policy evaluation (OPE) and local policy optimization in the settings of i.i.d. and global confounders. Theoretical and empirical results confirm the validity and viability of these methods.

Learning Mixtures of Markov Chains and MDPs

We present an algorithm for use in learning mixtures of both Markov chains (MCs) and Markov decision processes (offline latent MDPs) from trajectories, with roots dating back to the work of Vempala and Wang. This amounts to handling Markov chains with optional control input. The method is modular in nature and amounts to (1) a subspace estimation step, (2) spectral clustering of trajectories, and (3) a few iterations of the EM algorithm. We provide end-to-end performance guarantees where we only explicitly require the number of trajectories to be linear in states and the trajectory length to be linear in mixing time. Experimental results suggest it outperforms both EM (95.4% on average) and a previous method by Gupta et al. (54.1%), obtaining 100% permuted accuracy on an 8x8 gridworld.

Thompson Sampling for High-Dimensional Sparse Linear Contextual Bandits

We consider the stochastic linear contextual bandit problem with high-dimensional features. We analyze the Thompson sampling (TS) algorithm, using special classes of sparsity-inducing priors (e.g. spike-and-slab) to model the unknown parameter, and provide a nearly optimal upper bound on the expected cumulative regret. To the best of our knowledge, this is the first work that provides theoretical guarantees of Thompson sampling in high dimensional and sparse contextual bandits. For faster computation, we use spike-and-slab prior to model the unknown parameter and variational inference instead of MCMC to approximate the posterior distribution. Extensive simulations demonstrate improved performance of our proposed algorithm over existing ones.

Probabilistically Robust PAC Learning

Recently, Robey et al. propose a notion of probabilistic robustness, which, at a high-level, requires a classifier to be robust to most but not all perturbations. They show that for certain hypothesis classes where proper learning under worst-case robustness is \textit{not} possible, proper learning under probabilistic robustness \textit{is} possible with sample complexity exponentially smaller than in the worst-case robustness setting. This motivates the question of whether proper learning under probabilistic robustness is always possible. In this paper, we show that this is \textit{not} the case. We exhibit examples of hypothesis classes $\mathcal{H}$ with finite VC dimension that are \textit{not} probabilistically robustly PAC learnable with \textit{any} proper learning rule. However, if we compare the output of the learner to the best hypothesis for a slightly \textit{stronger} level of probabilistic robustness, we show that not only is proper learning \textit{always} possible, but it is possible via empirical risk minimization.

Adaptive Learning for Discovery

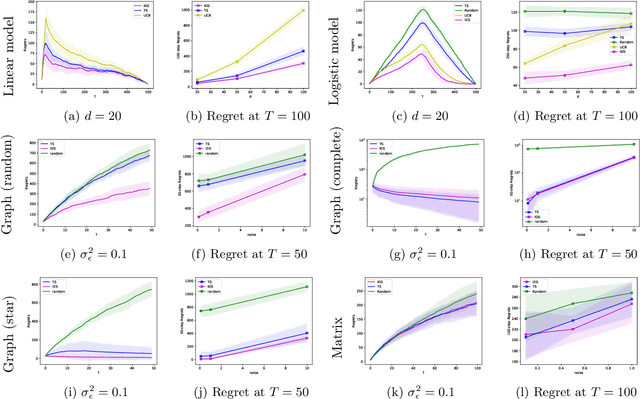
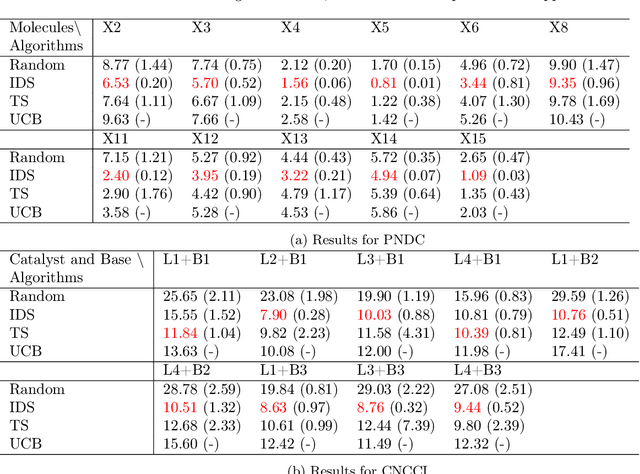
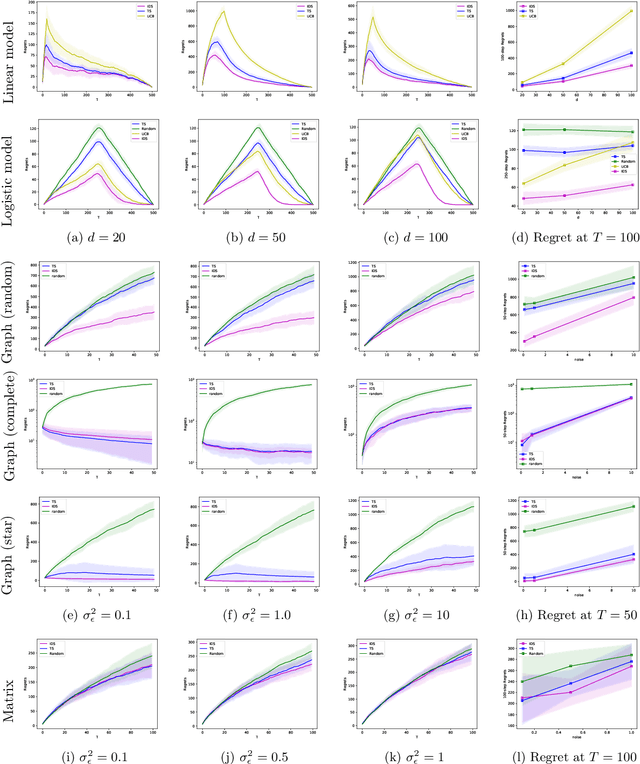
In this paper, we study a sequential decision-making problem, called Adaptive Sampling for Discovery (ASD). Starting with a large unlabeled dataset, algorithms for ASD adaptively label the points with the goal to maximize the sum of responses. This problem has wide applications to real-world discovery problems, for example drug discovery with the help of machine learning models. ASD algorithms face the well-known exploration-exploitation dilemma. The algorithm needs to choose points that yield information to improve model estimates but it also needs to exploit the model. We rigorously formulate the problem and propose a general information-directed sampling (IDS) algorithm. We provide theoretical guarantees for the performance of IDS in linear, graph and low-rank models. The benefits of IDS are shown in both simulation experiments and real-data experiments for discovering chemical reaction conditions.