Perceptron like Algorithms for Online Learning to Rank

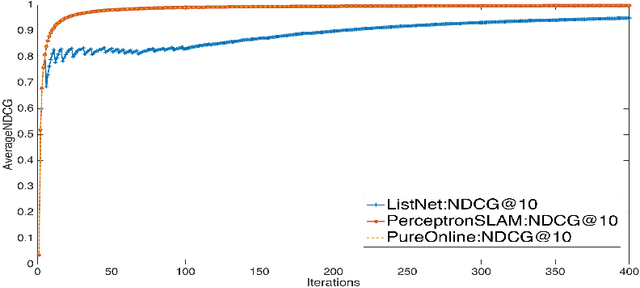
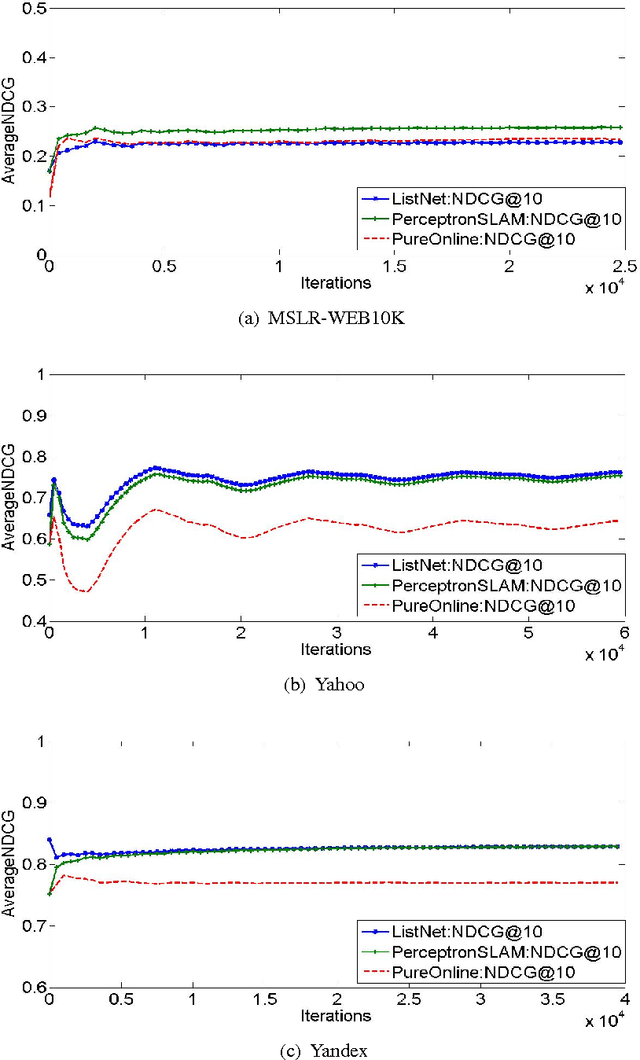
Perceptron is a classic online algorithm for learning a classification function. In this paper, we provide a novel extension of the perceptron algorithm to the learning to rank problem in information retrieval. We consider popular listwise performance measures such as Normalized Discounted Cumulative Gain (NDCG) and Average Precision (AP). A modern perspective on perceptron for classification is that it is simply an instance of online gradient descent (OGD), during mistake rounds, using the hinge loss function. Motivated by this interpretation, we propose a novel family of listwise, large margin ranking surrogates. Members of this family can be thought of as analogs of the hinge loss. Exploiting a certain self-bounding property of the proposed family, we provide a guarantee on the cumulative NDCG (or AP) induced loss incurred by our perceptron-like algorithm. We show that, if there exists a perfect oracle ranker which can correctly rank each instance in an online sequence of ranking data, with some margin, the cumulative loss of perceptron algorithm on that sequence is bounded by a constant, irrespective of the length of the sequence. This result is reminiscent of Novikoff's convergence theorem for the classification perceptron. Moreover, we prove a lower bound on the cumulative loss achievable by any deterministic algorithm, under the assumption of existence of perfect oracle ranker. The lower bound shows that our perceptron bound is not tight, and we propose another, \emph{purely online}, algorithm which achieves the lower bound. We provide empirical results on simulated and large commercial datasets to corroborate our theoretical results.

Mixture Proportion Estimation via Kernel Embedding of Distributions

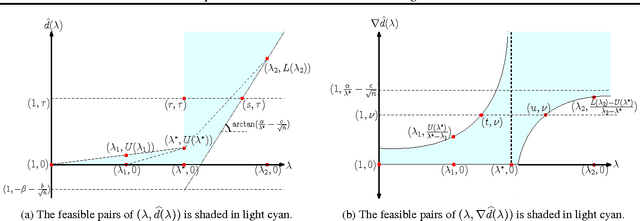
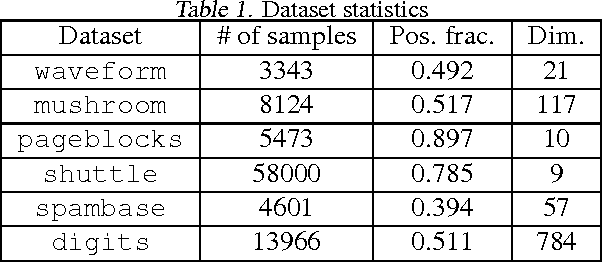
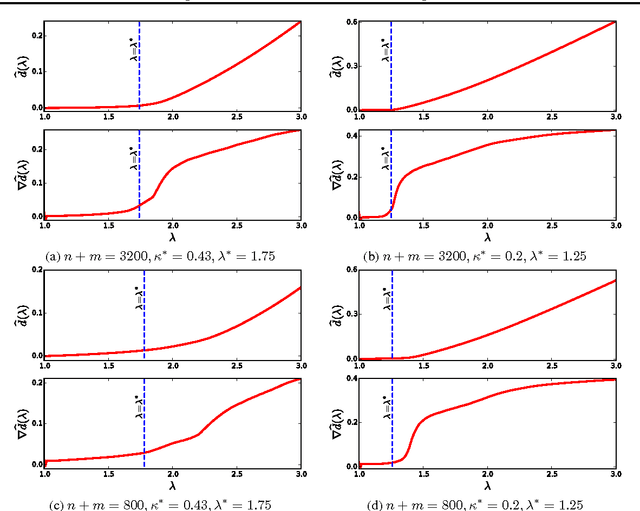
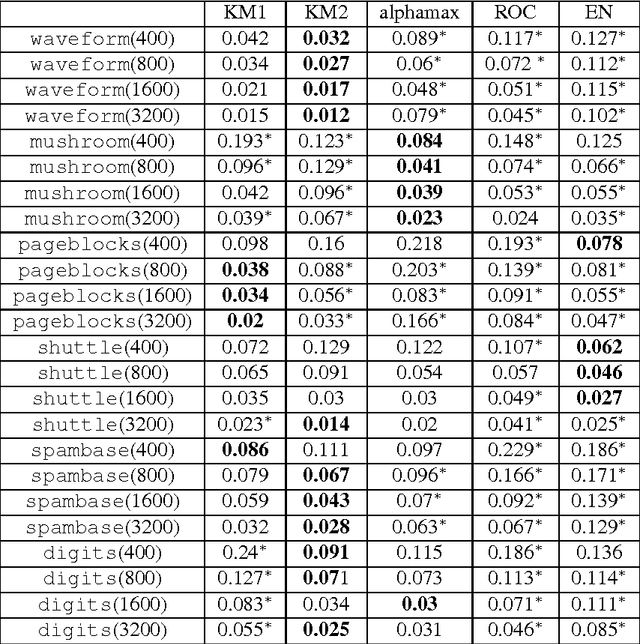
Mixture proportion estimation (MPE) is the problem of estimating the weight of a component distribution in a mixture, given samples from the mixture and component. This problem constitutes a key part in many "weakly supervised learning" problems like learning with positive and unlabelled samples, learning with label noise, anomaly detection and crowdsourcing. While there have been several methods proposed to solve this problem, to the best of our knowledge no efficient algorithm with a proven convergence rate towards the true proportion exists for this problem. We fill this gap by constructing a provably correct algorithm for MPE, and derive convergence rates under certain assumptions on the distribution. Our method is based on embedding distributions onto an RKHS, and implementing it only requires solving a simple convex quadratic programming problem a few times. We run our algorithm on several standard classification datasets, and demonstrate that it performs comparably to or better than other algorithms on most datasets.

Online Ranking with Top-1 Feedback

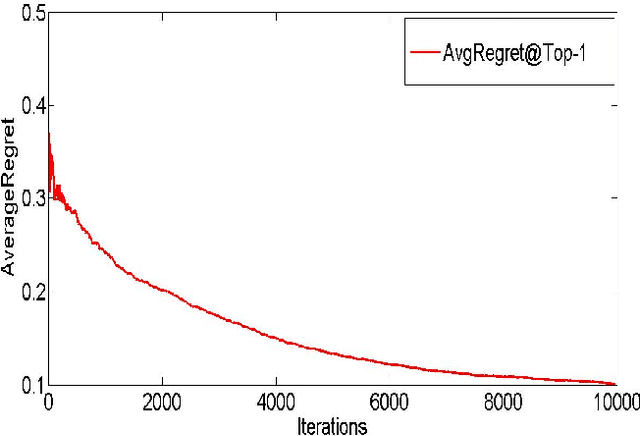
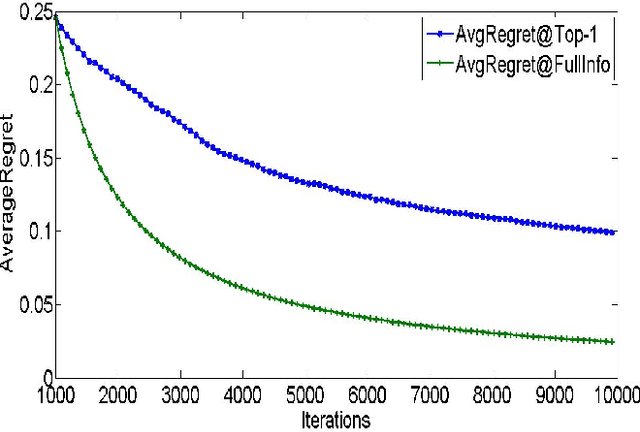
We consider a setting where a system learns to rank a fixed set of $m$ items. The goal is produce good item rankings for users with diverse interests who interact online with the system for $T$ rounds. We consider a novel top-$1$ feedback model: at the end of each round, the relevance score for only the top ranked object is revealed. However, the performance of the system is judged on the entire ranked list. We provide a comprehensive set of results regarding learnability under this challenging setting. For PairwiseLoss and DCG, two popular ranking measures, we prove that the minimax regret is $\Theta(T^{2/3})$. Moreover, the minimax regret is achievable using an efficient strategy that only spends $O(m \log m)$ time per round. The same efficient strategy achieves $O(T^{2/3})$ regret for Precision@$k$. Surprisingly, we show that for normalized versions of these ranking measures, i.e., AUC, NDCG \& MAP, no online ranking algorithm can have sublinear regret.

Generalization error bounds for learning to rank: Does the length of document lists matter?

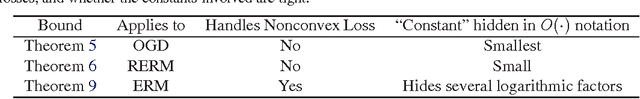
We consider the generalization ability of algorithms for learning to rank at a query level, a problem also called subset ranking. Existing generalization error bounds necessarily degrade as the size of the document list associated with a query increases. We show that such a degradation is not intrinsic to the problem. For several loss functions, including the cross-entropy loss used in the well known ListNet method, there is \emph{no} degradation in generalization ability as document lists become longer. We also provide novel generalization error bounds under $\ell_1$ regularization and faster convergence rates if the loss function is smooth.

Online Learning to Rank with Feedback at the Top

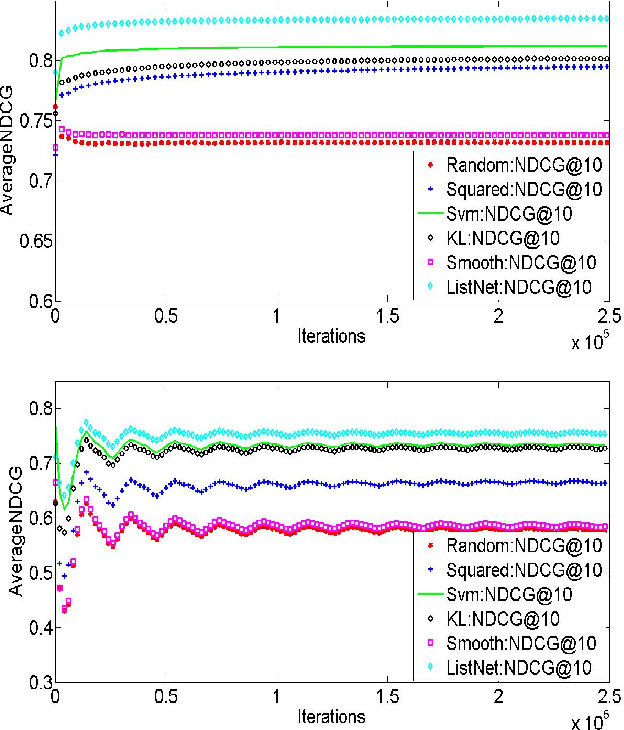
We consider an online learning to rank setting in which, at each round, an oblivious adversary generates a list of $m$ documents, pertaining to a query, and the learner produces scores to rank the documents. The adversary then generates a relevance vector and the learner updates its ranker according to the feedback received. We consider the setting where the feedback is restricted to be the relevance levels of only the top $k$ documents in the ranked list for $k \ll m$. However, the performance of learner is judged based on the unrevealed full relevance vectors, using an appropriate learning to rank loss function. We develop efficient algorithms for well known losses in the pointwise, pairwise and listwise families. We also prove that no online algorithm can have sublinear regret, with top-1 feedback, for any loss that is calibrated with respect to NDCG. We apply our algorithms on benchmark datasets demonstrating efficient online learning of a ranking function from highly restricted feedback.

Handling Class Imbalance in Link Prediction using Learning to Rank Techniques

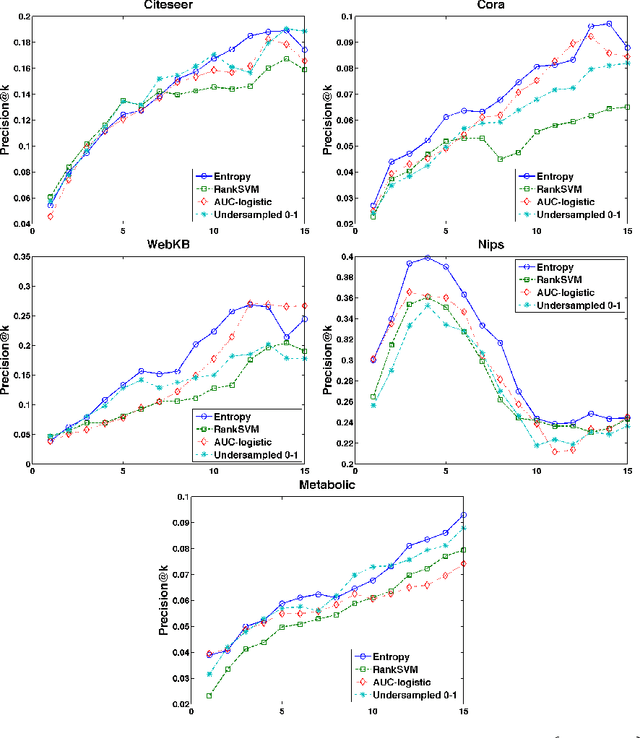
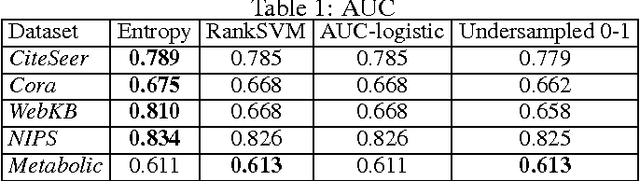
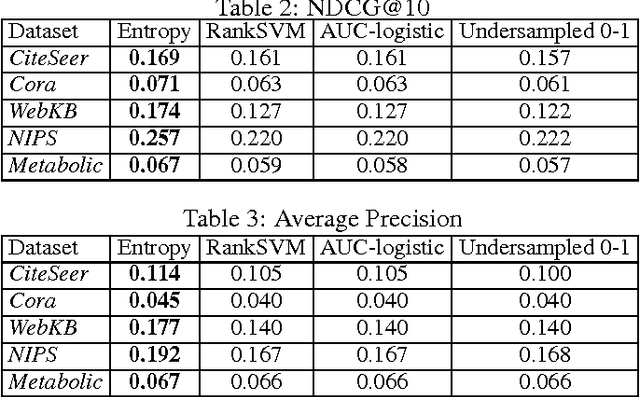
We consider the link prediction problem in a partially observed network, where the objective is to make predictions in the unobserved portion of the network. Many existing methods reduce link prediction to binary classification problem. However, the dominance of absent links in real world networks makes misclassification error a poor performance metric. Instead, researchers have argued for using ranking performance measures, like AUC, AP and NDCG, for evaluation. Our main contribution is to recast the link prediction problem as a learning to rank problem and use effective learning to rank techniques directly during training. This is in contrast to existing work that uses ranking measures only during evaluation. Our approach is able to deal with the class imbalance problem by using effective, scalable learning to rank techniques during training. Furthermore, our approach allows us to combine network topology and node features. As a demonstration of our general approach, we develop a link prediction method by optimizing the cross-entropy surrogate, originally used in the popular ListNet ranking algorithm. We conduct extensive experiments on publicly available co-authorship, citation and metabolic networks to demonstrate the merits of our method.

Spectral Smoothing via Random Matrix Perturbations

We consider stochastic smoothing of spectral functions of matrices using perturbations commonly studied in random matrix theory. We show that a spectral function remains spectral when smoothed using a unitarily invariant perturbation distribution. We then derive state-of-the-art smoothing bounds for the maximum eigenvalue function using the Gaussian Orthogonal Ensemble (GOE). Smoothing the maximum eigenvalue function is important for applications in semidefinite optimization and online learning. As a direct consequence of our GOE smoothing results, we obtain an $O((N \log N)^{1/4} \sqrt{T})$ expected regret bound for the online variance minimization problem using an algorithm that performs only a single maximum eigenvector computation per time step. Here $T$ is the number of rounds and $N$ is the matrix dimension. Our algorithm and its analysis also extend to the more general online PCA problem where the learner has to output a rank $k$ subspace. The algorithm just requires computing $k$ maximum eigenvectors per step and enjoys an $O(k (N \log N)^{1/4} \sqrt{T})$ expected regret bound.

Fighting Bandits with a New Kind of Smoothness

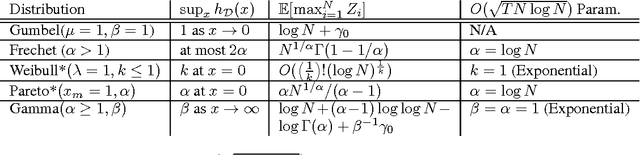
We define a novel family of algorithms for the adversarial multi-armed bandit problem, and provide a simple analysis technique based on convex smoothing. We prove two main results. First, we show that regularization via the \emph{Tsallis entropy}, which includes EXP3 as a special case, achieves the $\Theta(\sqrt{TN})$ minimax regret. Second, we show that a wide class of perturbation methods achieve a near-optimal regret as low as $O(\sqrt{TN \log N})$ if the perturbation distribution has a bounded hazard rate. For example, the Gumbel, Weibull, Frechet, Pareto, and Gamma distributions all satisfy this key property.

Learning Exponential Families in High-Dimensions: Strong Convexity and Sparsity

The versatility of exponential families, along with their attendant convexity properties, make them a popular and effective statistical model. A central issue is learning these models in high-dimensions, such as when there is some sparsity pattern of the optimal parameter. This work characterizes a certain strong convexity property of general exponential families, which allow their generalization ability to be quantified. In particular, we show how this property can be used to analyze generic exponential families under L_1 regularization.

Consistent Algorithms for Multiclass Classification with a Reject Option

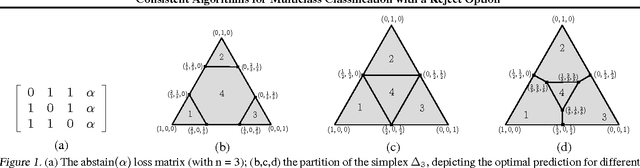
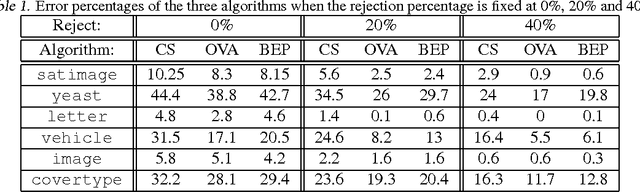
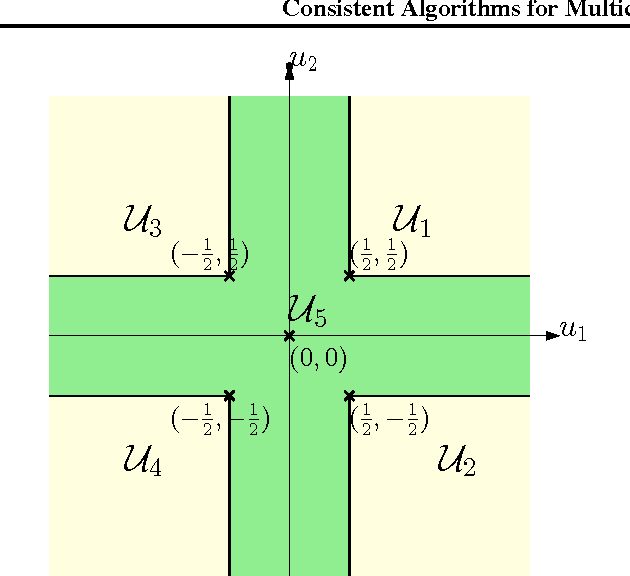
We consider the problem of $n$-class classification ($n\geq 2$), where the classifier can choose to abstain from making predictions at a given cost, say, a factor $\alpha$ of the cost of misclassification. Designing consistent algorithms for such $n$-class classification problems with a `reject option' is the main goal of this paper, thereby extending and generalizing previously known results for $n=2$. We show that the Crammer-Singer surrogate and the one vs all hinge loss, albeit with a different predictor than the standard argmax, yield consistent algorithms for this problem when $\alpha=\frac{1}{2}$. More interestingly, we design a new convex surrogate that is also consistent for this problem when $\alpha=\frac{1}{2}$ and operates on a much lower dimensional space ($\log(n)$ as opposed to $n$). We also generalize all three surrogates to be consistent for any $\alpha\in[0, \frac{1}{2}]$.