Learning to fail: Predicting fracture evolution in brittle materials using recurrent graph convolutional neural networks

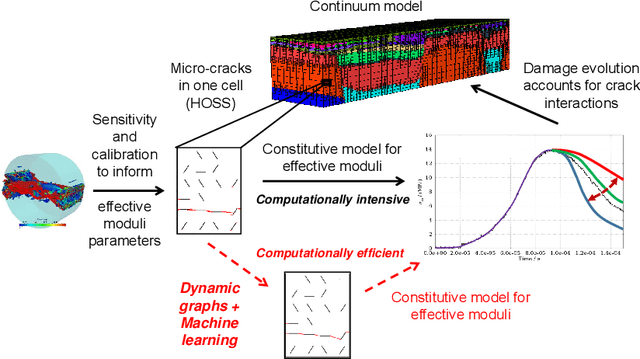
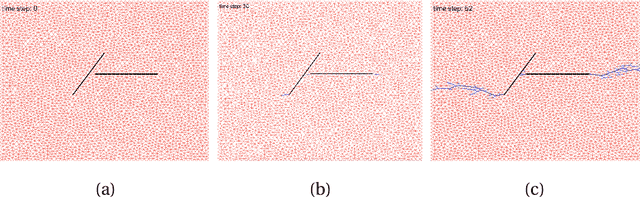
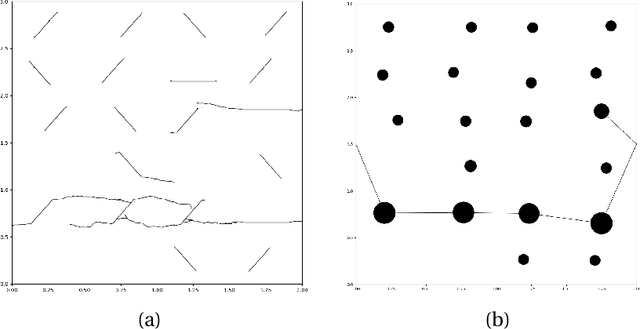
Understanding dynamic fracture propagation is essential to predicting how brittle materials fail. Various mathematical models and computational applications have been developed to predict fracture evolution and coalescence, including finite-discrete element methods such as the Hybrid Optimization Software Suite (HOSS). While such methods achieve high fidelity results, they can be computationally prohibitive: a single simulation takes hours to run, and thousands of simulations are required for a statistically meaningful ensemble. We propose a machine learning approach that, once trained on data from HOSS simulations, can predict fracture growth statistics within seconds. Our method uses deep learning, exploiting the capabilities of a graph convolutional network to recognize features of the fracturing material, along with a recurrent neural network to model the evolution of these features. In this way, we simultaneously generate predictions for qualitatively distinct material properties. Our prediction for total damage in a coalesced fracture, at the final simulation time step, is within 3% of its actual value, and our prediction for total length of a coalesced fracture is within 2%. We also develop a novel form of data augmentation that compensates for the modest size of our training data, and an ensemble learning approach that enables us to predict when the material fails, with a mean absolute error of approximately 15%.

Unsupervised vehicle recognition using incremental reseeding of acoustic signatures

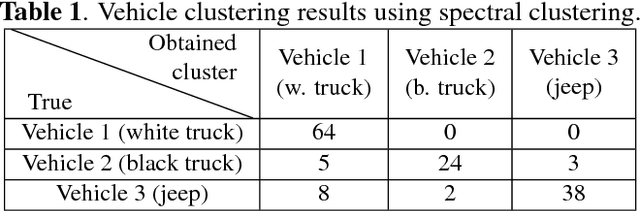
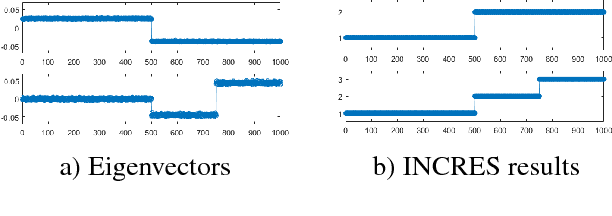
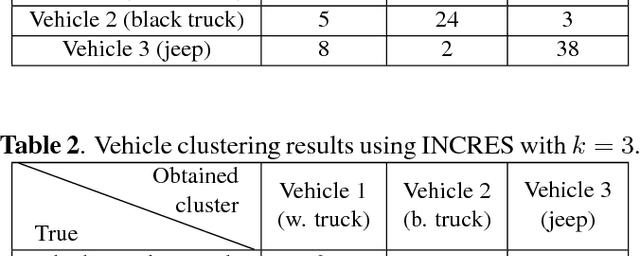
Vehicle recognition and classification have broad applications, ranging from traffic flow management to military target identification. We demonstrate an unsupervised method for automated identification of moving vehicles from roadside audio sensors. Using a short-time Fourier transform to decompose audio signals, we treat the frequency signature in each time window as an individual data point. We then use a spectral embedding for dimensionality reduction. Based on the leading eigenvectors, we relate the performance of an incremental reseeding algorithm to that of spectral clustering. We find that incremental reseeding accurately identifies individual vehicles using their acoustic signatures.

Dimensionality reduction for acoustic vehicle classification with spectral embedding

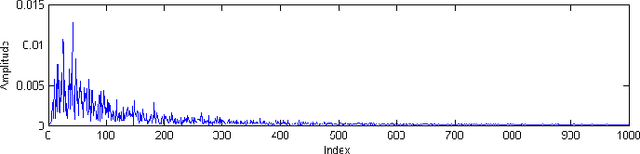
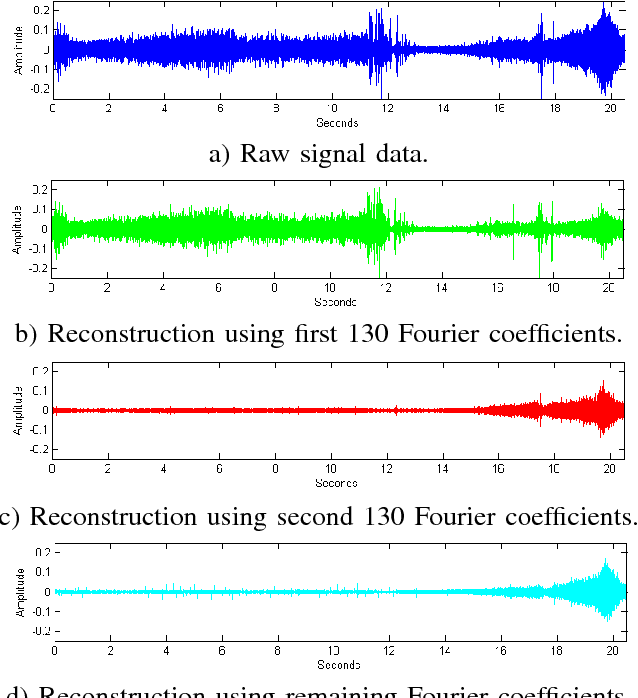
We propose a method for recognizing moving vehicles, using data from roadside audio sensors. This problem has applications ranging widely, from traffic analysis to surveillance. We extract a frequency signature from the audio signal using a short-time Fourier transform, and treat each time window as an individual data point to be classified. By applying a spectral embedding, we decrease the dimensionality of the data sufficiently for K-nearest neighbors to provide accurate vehicle identification.

Machine learning for graph-based representations of three-dimensional discrete fracture networks

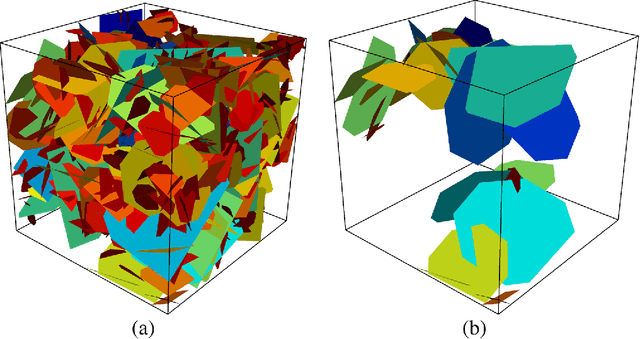
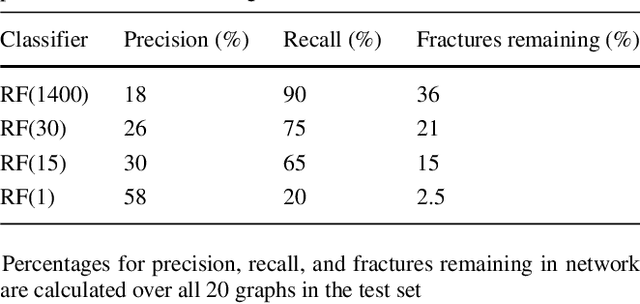
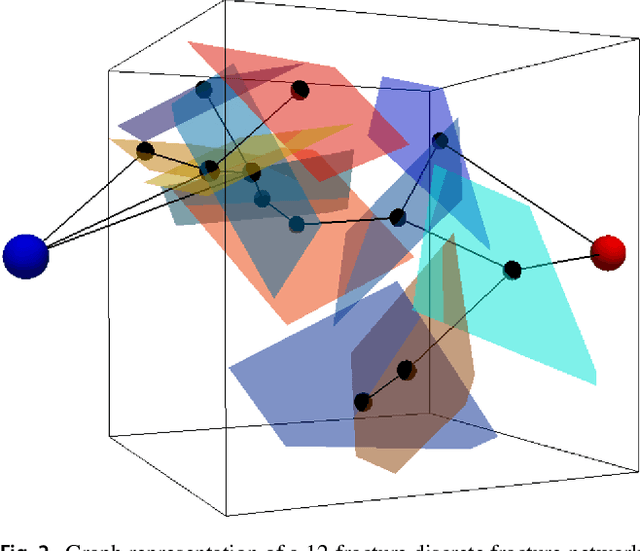
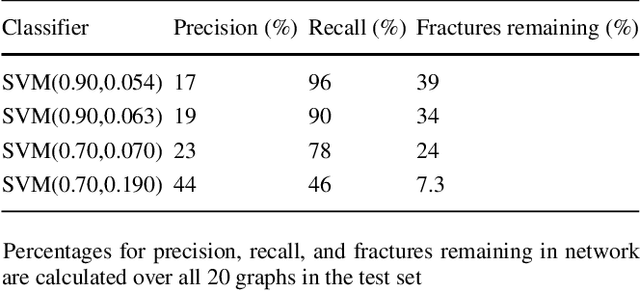
Structural and topological information play a key role in modeling flow and transport through fractured rock in the subsurface. Discrete fracture network (DFN) computational suites such as dfnWorks are designed to simulate flow and transport in such porous media. Flow and transport calculations reveal that a small backbone of fractures exists, where most flow and transport occurs. Restricting the flowing fracture network to this backbone provides a significant reduction in the network's effective size. However, the particle tracking simulations needed to determine the reduction are computationally intensive. Such methods may be impractical for large systems or for robust uncertainty quantification of fracture networks, where thousands of forward simulations are needed to bound system behavior. In this paper, we develop an alternative network reduction approach to characterizing transport in DFNs, by combining graph theoretical and machine learning methods. We consider a graph representation where nodes signify fractures and edges denote their intersections. Using random forest and support vector machines, we rapidly identify a subnetwork that captures the flow patterns of the full DFN, based primarily on node centrality features in the graph. Our supervised learning techniques train on particle-tracking backbone paths found by dfnWorks, but run in negligible time compared to those simulations. We find that our predictions can reduce the network to approximately 20% of its original size, while still generating breakthrough curves consistent with those of the original network.

Improving Image Clustering using Sparse Text and the Wisdom of the Crowds

We propose a method to improve image clustering using sparse text and the wisdom of the crowds. In particular, we present a method to fuse two different kinds of document features, image and text features, and use a common dictionary or "wisdom of the crowds" as the connection between the two different kinds of documents. With the proposed fusion matrix, we use topic modeling via non-negative matrix factorization to cluster documents.

Spectral Clustering with Epidemic Diffusion

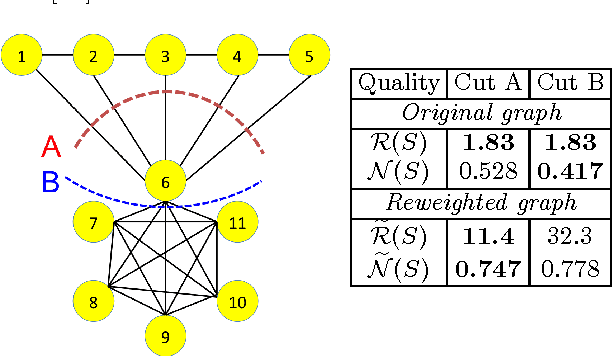
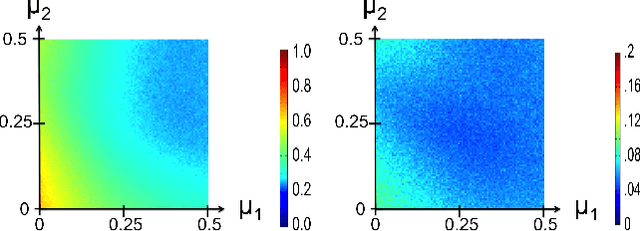
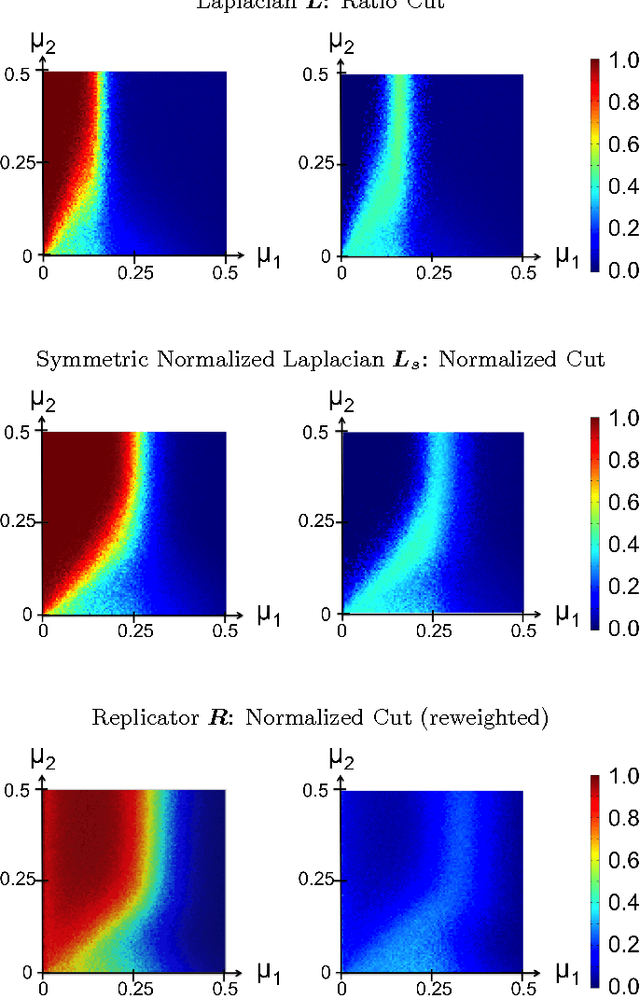
Spectral clustering is widely used to partition graphs into distinct modules or communities. Existing methods for spectral clustering use the eigenvalues and eigenvectors of the graph Laplacian, an operator that is closely associated with random walks on graphs. We propose a new spectral partitioning method that exploits the properties of epidemic diffusion. An epidemic is a dynamic process that, unlike the random walk, simultaneously transitions to all the neighbors of a given node. We show that the replicator, an operator describing epidemic diffusion, is equivalent to the symmetric normalized Laplacian of a reweighted graph with edges reweighted by the eigenvector centralities of their incident nodes. Thus, more weight is given to edges connecting more central nodes. We describe a method that partitions the nodes based on the componentwise ratio of the replicator's second eigenvector to the first, and compare its performance to traditional spectral clustering techniques on synthetic graphs with known community structure. We demonstrate that the replicator gives preference to dense, clique-like structures, enabling it to more effectively discover communities that may be obscured by dense intercommunity linking.

Multiclass Semi-Supervised Learning on Graphs using Ginzburg-Landau Functional Minimization

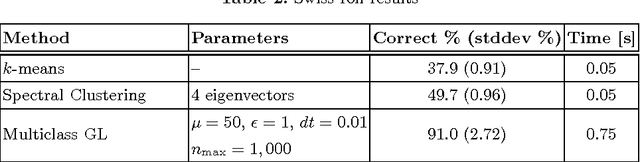
We present a graph-based variational algorithm for classification of high-dimensional data, generalizing the binary diffuse interface model to the case of multiple classes. Motivated by total variation techniques, the method involves minimizing an energy functional made up of three terms. The first two terms promote a stepwise continuous classification function with sharp transitions between classes, while preserving symmetry among the class labels. The third term is a data fidelity term, allowing us to incorporate prior information into the model in a semi-supervised framework. The performance of the algorithm on synthetic data, as well as on the COIL and MNIST benchmark datasets, is competitive with state-of-the-art graph-based multiclass segmentation methods.

Multiclass Diffuse Interface Models for Semi-Supervised Learning on Graphs

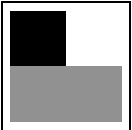
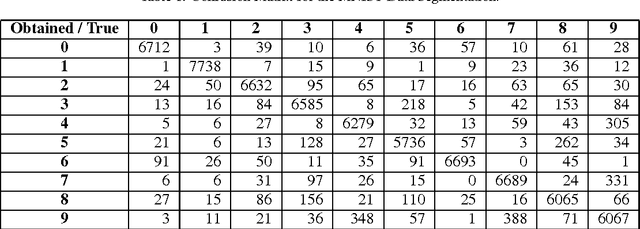
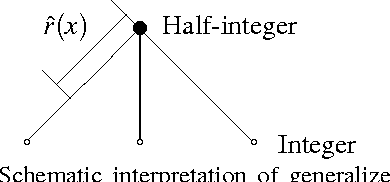
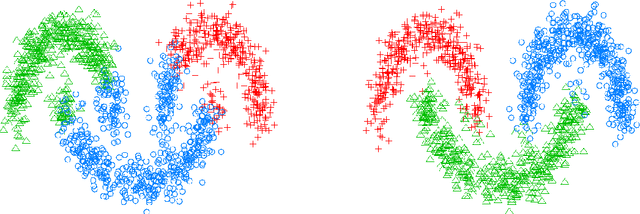
We present a graph-based variational algorithm for multiclass classification of high-dimensional data, motivated by total variation techniques. The energy functional is based on a diffuse interface model with a periodic potential. We augment the model by introducing an alternative measure of smoothness that preserves symmetry among the class labels. Through this modification of the standard Laplacian, we construct an efficient multiclass method that allows for sharp transitions between classes. The experimental results demonstrate that our approach is competitive with the state of the art among other graph-based algorithms.

Spines of Random Constraint Satisfaction Problems: Definition and Connection with Computational Complexity

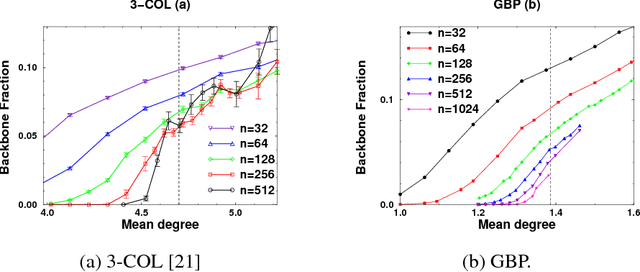
We study the connection between the order of phase transitions in combinatorial problems and the complexity of decision algorithms for such problems. We rigorously show that, for a class of random constraint satisfaction problems, a limited connection between the two phenomena indeed exists. Specifically, we extend the definition of the spine order parameter of Bollobas et al. to random constraint satisfaction problems, rigorously showing that for such problems a discontinuity of the spine is associated with a $2^{\Omega(n)}$ resolution complexity (and thus a $2^{\Omega(n)}$ complexity of DPLL algorithms) on random instances. The two phenomena have a common underlying cause: the emergence of ``large'' (linear size) minimally unsatisfiable subformulas of a random formula at the satisfiability phase transition. We present several further results that add weight to the intuition that random constraint satisfaction problems with a sharp threshold and a continuous spine are ``qualitatively similar to random 2-SAT''. Finally, we argue that it is the spine rather than the backbone parameter whose continuity has implications for the decision complexity of combinatorial problems, and we provide experimental evidence that the two parameters can behave in a different manner.

Extremal Optimization: an Evolutionary Local-Search Algorithm

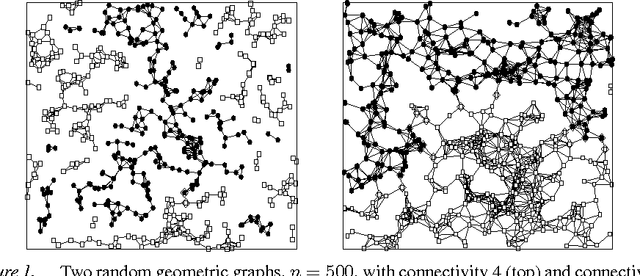
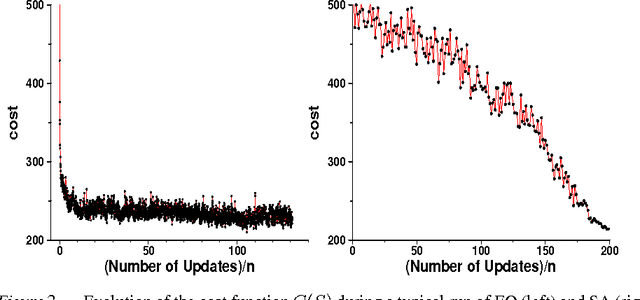
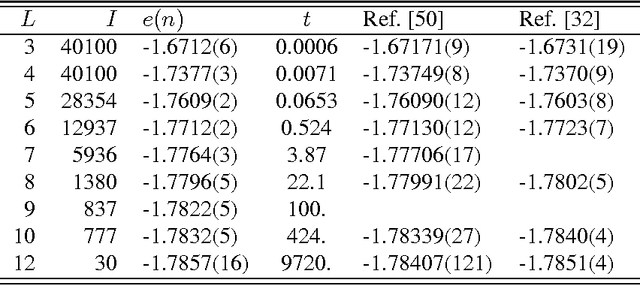
A recently introduced general-purpose heuristic for finding high-quality solutions for many hard optimization problems is reviewed. The method is inspired by recent progress in understanding far-from-equilibrium phenomena in terms of {\em self-organized criticality,} a concept introduced to describe emergent complexity in physical systems. This method, called {\em extremal optimization,} successively replaces the value of extremely undesirable variables in a sub-optimal solution with new, random ones. Large, avalanche-like fluctuations in the cost function self-organize from this dynamics, effectively scaling barriers to explore local optima in distant neighborhoods of the configuration space while eliminating the need to tune parameters. Drawing upon models used to simulate the dynamics of granular media, evolution, or geology, extremal optimization complements approximation methods inspired by equilibrium statistical physics, such as {\em simulated annealing}. It may be but one example of applying new insights into {\em non-equilibrium phenomena} systematically to hard optimization problems. This method is widely applicable and so far has proved competitive with -- and even superior to -- more elaborate general-purpose heuristics on testbeds of constrained optimization problems with up to $10^5$ variables, such as bipartitioning, coloring, and satisfiability. Analysis of a suitable model predicts the only free parameter of the method in accordance with all experimental results.