Shift Before You Learn: Enabling Low-Rank Representations in Reinforcement Learning

Low-rank structure is a common implicit assumption in many modern reinforcement learning (RL) algorithms. For instance, reward-free and goal-conditioned RL methods often presume that the successor measure admits a low-rank representation. In this work, we challenge this assumption by first remarking that the successor measure itself is not low-rank. Instead, we demonstrate that a low-rank structure naturally emerges in the shifted successor measure, which captures the system dynamics after bypassing a few initial transitions. We provide finite-sample performance guarantees for the entry-wise estimation of a low-rank approximation of the shifted successor measure from sampled entries. Our analysis reveals that both the approximation and estimation errors are primarily governed by the so-called spectral recoverability of the corresponding matrix. To bound this parameter, we derive a new class of functional inequalities for Markov chains that we call Type II Poincar\'e inequalities and from which we can quantify the amount of shift needed for effective low-rank approximation and estimation. This analysis shows in particular that the required shift depends on decay of the high-order singular values of the shifted successor measure and is hence typically small in practice. Additionally, we establish a connection between the necessary shift and the local mixing properties of the underlying dynamical system, which provides a natural way of selecting the shift. Finally, we validate our theoretical findings with experiments, and demonstrate that shifting the successor measure indeed leads to improved performance in goal-conditioned RL.

Nearly Optimal Latent State Decoding in Block MDPs

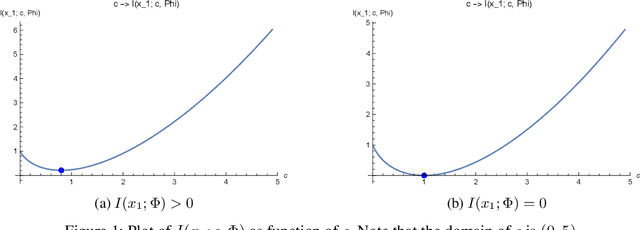
We investigate the problems of model estimation and reward-free learning in episodic Block MDPs. In these MDPs, the decision maker has access to rich observations or contexts generated from a small number of latent states. We are first interested in estimating the latent state decoding function (the mapping from the observations to latent states) based on data generated under a fixed behavior policy. We derive an information-theoretical lower bound on the error rate for estimating this function and present an algorithm approaching this fundamental limit. In turn, our algorithm also provides estimates of all the components of the MDP. We then study the problem of learning near-optimal policies in the reward-free framework. Based on our efficient model estimation algorithm, we show that we can infer a policy converging (as the number of collected samples grows large) to the optimal policy at the best possible rate. Interestingly, our analysis provides necessary and sufficient conditions under which exploiting the block structure yields improvements in the sample complexity for identifying near-optimal policies. When these conditions are met, the sample complexity in the minimax reward-free setting is improved by a multiplicative factor $n$, where $n$ is the number of possible contexts.

Regret in Online Recommendation Systems

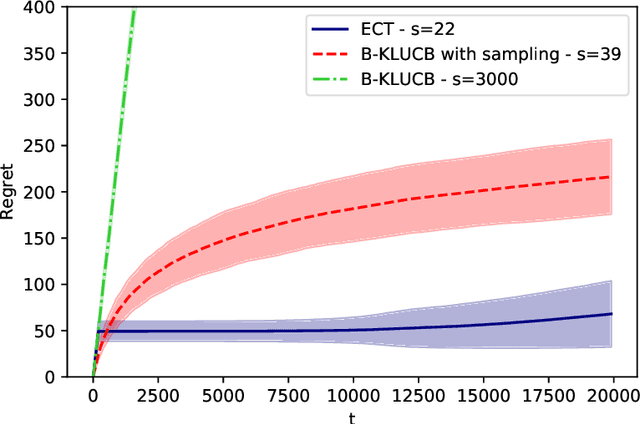
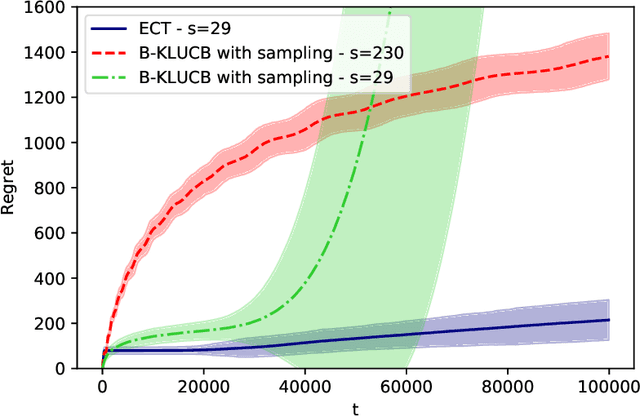
This paper proposes a theoretical analysis of recommendation systems in an online setting, where items are sequentially recommended to users over time. In each round, a user, randomly picked from a population of $m$ users, requests a recommendation. The decision-maker observes the user and selects an item from a catalogue of $n$ items. Importantly, an item cannot be recommended twice to the same user. The probabilities that a user likes each item are unknown. The performance of the recommendation algorithm is captured through its regret, considering as a reference an Oracle algorithm aware of these probabilities. We investigate various structural assumptions on these probabilities: we derive for each structure regret lower bounds, and devise algorithms achieving these limits. Interestingly, our analysis reveals the relative weights of the different components of regret: the component due to the constraint of not presenting the same item twice to the same user, that due to learning the chances users like items, and finally that arising when learning the underlying structure.

Thresholded LASSO Bandit

In this paper, we revisit sparse stochastic contextual linear bandits. In these problems, feature vectors may be of large dimension $d$, but the reward function depends on a few, say $s_0$, of these features only. We present Thresholded LASSO bandit, an algorithm that (i) estimates the vector defining the reward function as well as its sparse support using the LASSO framework with thresholding, and (ii) selects an arm greedily according to this estimate projected on its support. The algorithm does not require prior knowledge of the sparsity index $s_0$. For this simple algorithm, we establish non-asymptotic regret upper bounds scaling as $\mathcal{O}( \log d + \sqrt{T\log T} )$ in general, and as $\mathcal{O}( \log d + \log T)$ under the so-called margin condition (a setting where arms are well separated). The regret of previous algorithms scales as $\mathcal{O}( \sqrt{T} \log (d T))$ and $\mathcal{O}( \log T \log d)$ in the two settings, respectively. Through numerical experiments, we confirm that our algorithm outperforms existing methods.