Weighted Spectral Embedding of Graphs

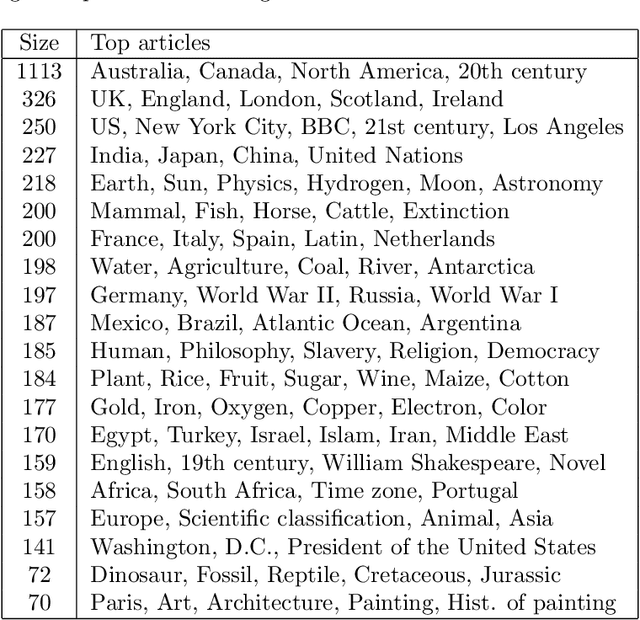
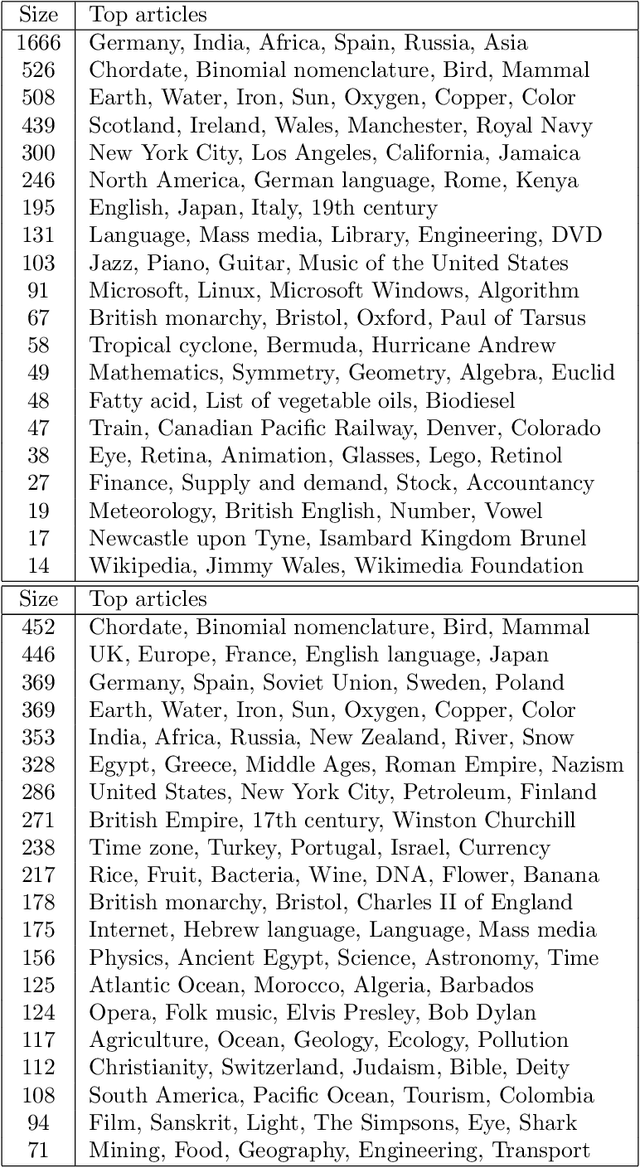
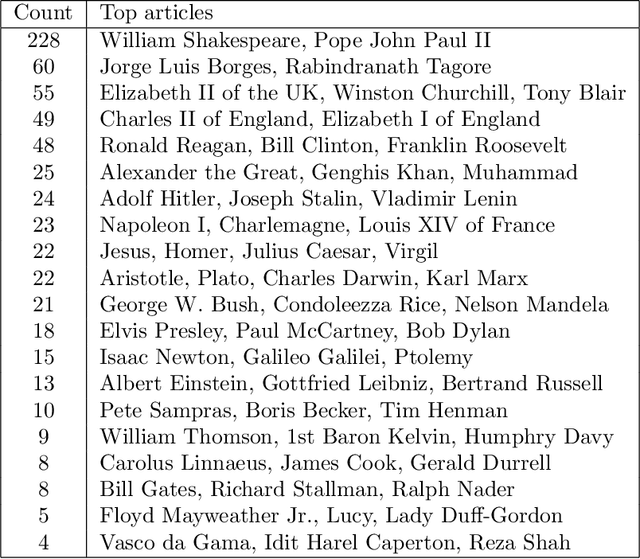
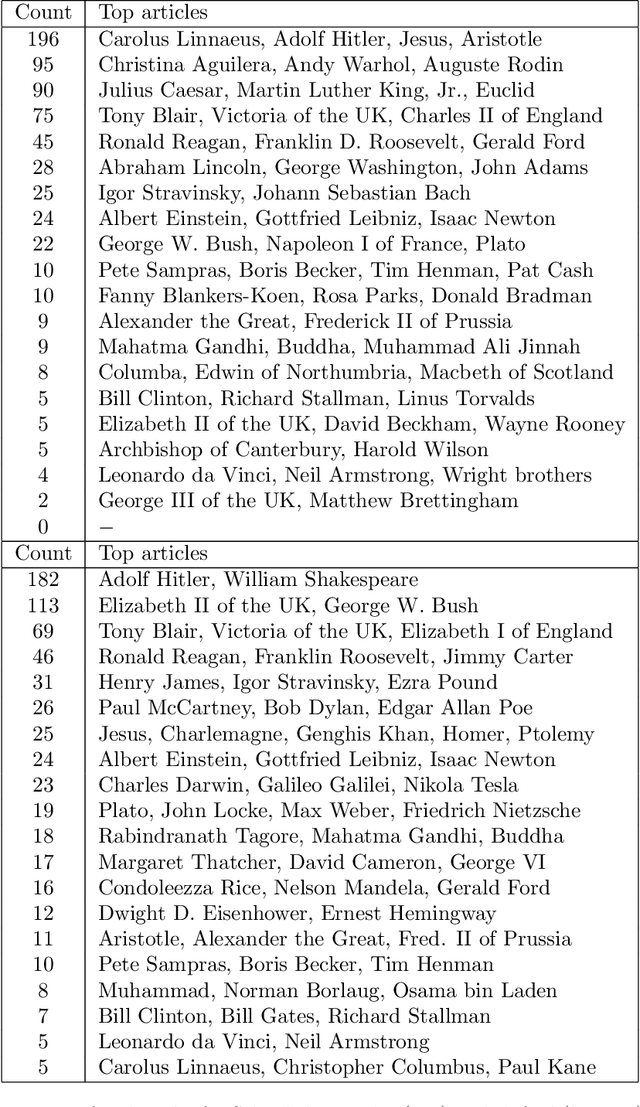
We present a novel spectral embedding of graphs that incorporates weights assigned to the nodes, quantifying their relative importance. This spectral embedding is based on the first eigenvectors of some properly normalized version of the Laplacian. We prove that these eigenvectors correspond to the configurations of lowest energy of an equivalent physical system, either mechanical or electrical, in which the weight of each node can be interpreted as its mass or its capacitance, respectively. Experiments on a real dataset illustrate the impact of weighting on the embedding.

Hierarchical Graph Clustering using Node Pair Sampling

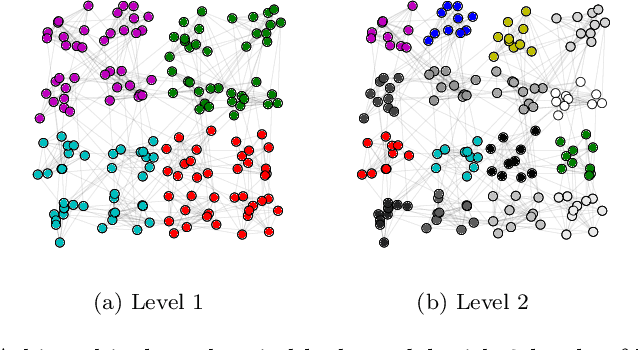
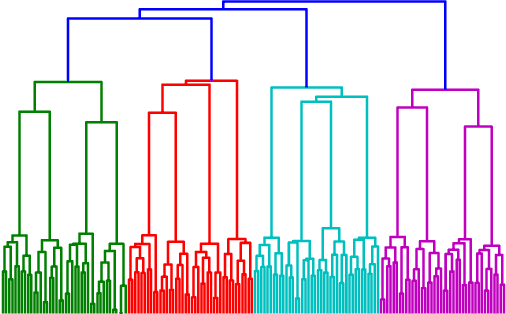
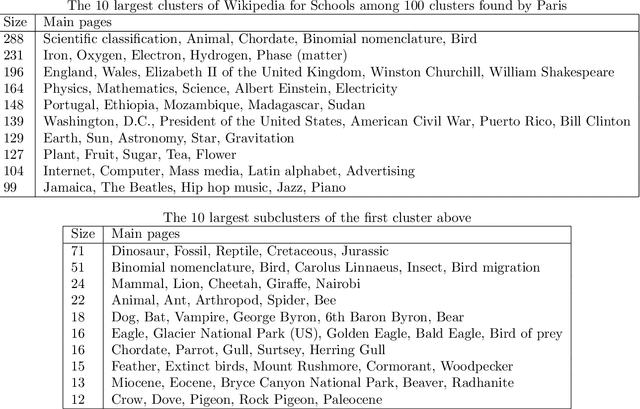
We present a novel hierarchical graph clustering algorithm inspired by modularity-based clustering techniques. The algorithm is agglomerative and based on a simple distance between clusters induced by the probability of sampling node pairs. We prove that this distance is reducible, which enables the use of the nearest-neighbor chain to speed up the agglomeration. The output of the algorithm is a regular dendrogram, which reveals the multi-scale structure of the graph. The results are illustrated on both synthetic and real datasets.

A Streaming Algorithm for Graph Clustering

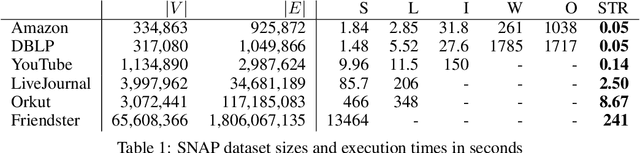
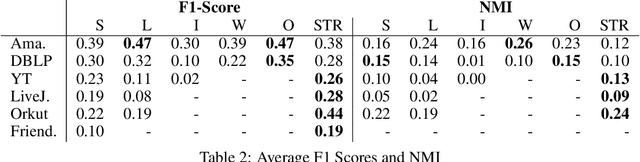
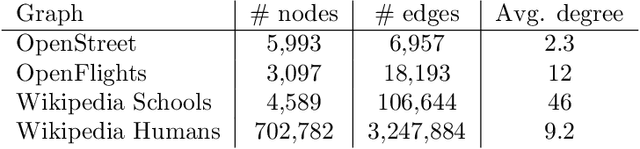
We introduce a novel algorithm to perform graph clustering in the edge streaming setting. In this model, the graph is presented as a sequence of edges that can be processed strictly once. Our streaming algorithm has an extremely low memory footprint as it stores only three integers per node and does not keep any edge in memory. We provide a theoretical justification of the design of the algorithm based on the modularity function, which is a usual metric to evaluate the quality of a graph partition. We perform experiments on massive real-life graphs ranging from one million to more than one billion edges and we show that this new algorithm runs more than ten times faster than existing algorithms and leads to similar or better detection scores on the largest graphs.