An Information-Geometric Approach to Artificial Curiosity

Learning in environments with sparse rewards remains a fundamental challenge in reinforcement learning. Artificial curiosity addresses this limitation through intrinsic rewards to guide exploration, however, the precise formulation of these rewards has remained elusive. Ideally, such rewards should depend on the agent's information about the environment, remaining agnostic to the representation of the information -- an invariance central to information geometry. Leveraging information geometry, we show that invariance under congruent Markov morphisms and the agent-environment interaction, uniquely constrains intrinsic rewards to concave functions of the reciprocal occupancy. Additional geometrically motivated restrictions effectively limits the candidates to those determined by a real parameter that governs the occupancy space geometry. Remarkably, special values of this parameter are found to correspond to count-based and maximum entropy exploration, revealing a geometric exploration-exploitation trade-off. This framework provides important constraints to the engineering of intrinsic reward while integrating foundational exploration methods into a single, cohesive model.

k-Means Maximum Entropy Exploration

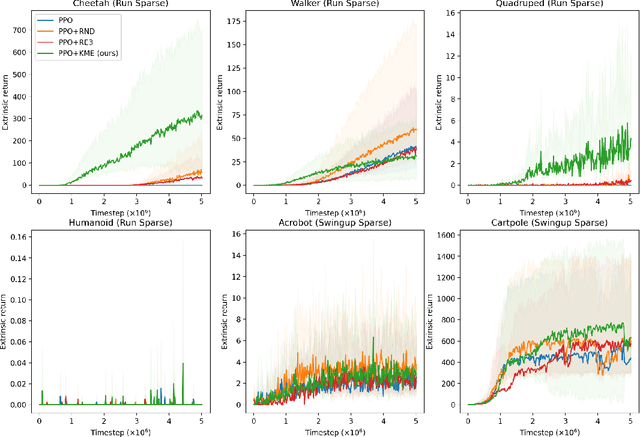
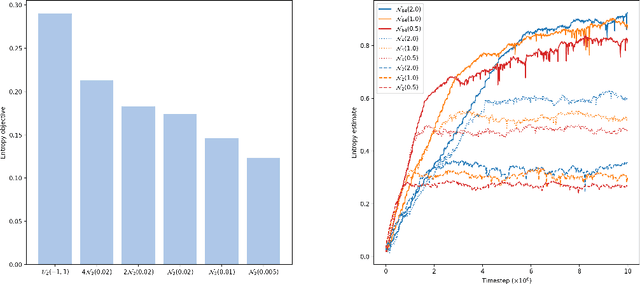
Exploration in high-dimensional, continuous spaces with sparse rewards is an open problem in reinforcement learning. Artificial curiosity algorithms address this by creating rewards that lead to exploration. Given a reinforcement learning algorithm capable of maximizing rewards, the problem reduces to finding an optimization objective consistent with exploration. Maximum entropy exploration uses the entropy of the state visitation distribution as such an objective. However, efficiently estimating the entropy of the state visitation distribution is challenging in high-dimensional, continuous spaces. We introduce an artificial curiosity algorithm based on lower bounding an approximation to the entropy of the state visitation distribution. The bound relies on a result we prove for non-parametric density estimation in arbitrary dimensions using k-means. We show that our approach is both computationally efficient and competitive on benchmarks for exploration in high-dimensional, continuous spaces, especially on tasks where reinforcement learning algorithms are unable to find rewards.