Exascale Deep Learning for Scientific Inverse Problems

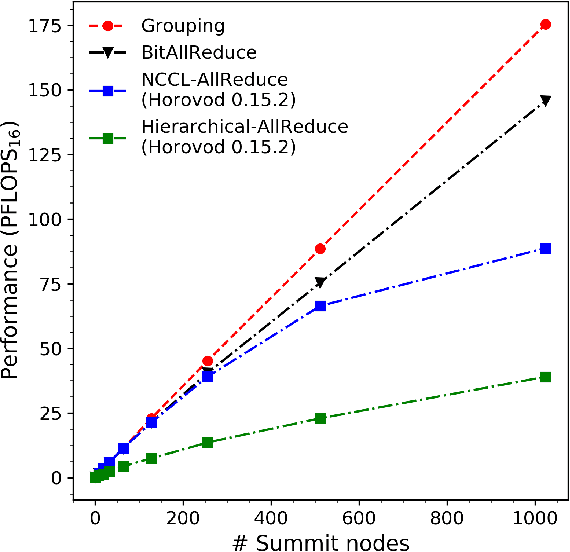
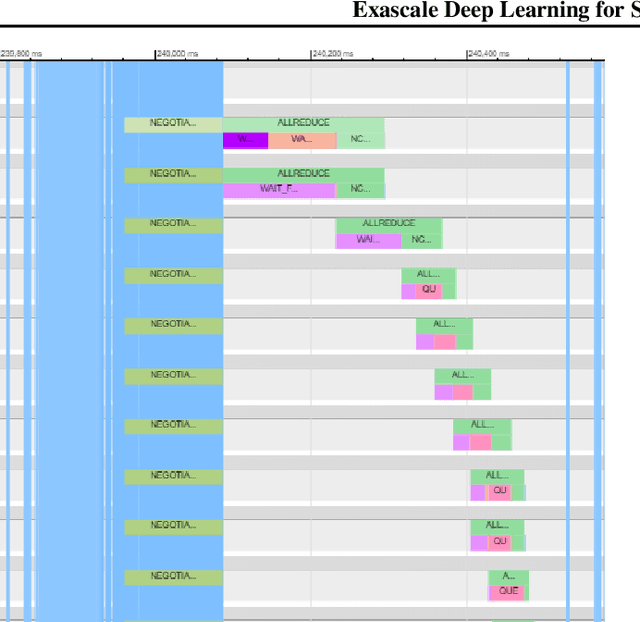
We introduce novel communication strategies in synchronous distributed Deep Learning consisting of decentralized gradient reduction orchestration and computational graph-aware grouping of gradient tensors. These new techniques produce an optimal overlap between computation and communication and result in near-linear scaling (0.93) of distributed training up to 27,600 NVIDIA V100 GPUs on the Summit Supercomputer. We demonstrate our gradient reduction techniques in the context of training a Fully Convolutional Neural Network to approximate the solution of a longstanding scientific inverse problem in materials imaging. The efficient distributed training on a dataset size of 0.5 PB, produces a model capable of an atomically-accurate reconstruction of materials, and in the process reaching a peak performance of 2.15(4) EFLOPS$_{16}$.

An Intriguing Failing of Convolutional Neural Networks and the CoordConv Solution

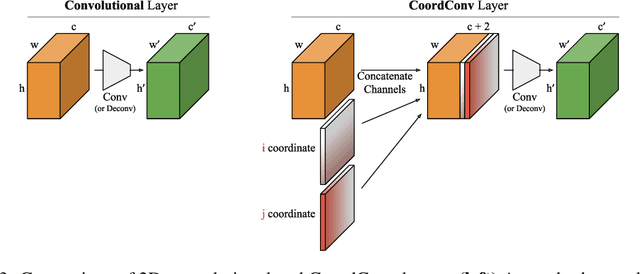
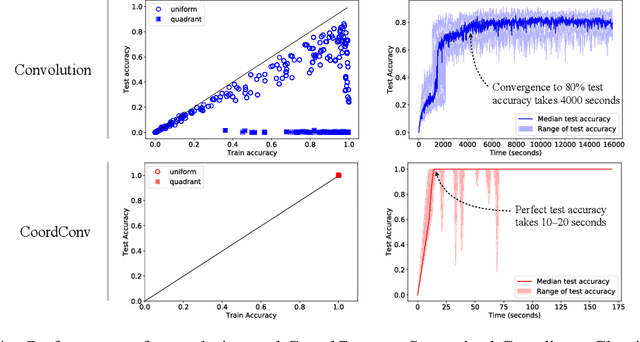
Few ideas have enjoyed as large an impact on deep learning as convolution. For any problem involving pixels or spatial representations, common intuition holds that convolutional neural networks may be appropriate. In this paper we show a striking counterexample to this intuition via the seemingly trivial coordinate transform problem, which simply requires learning a mapping between coordinates in (x,y) Cartesian space and one-hot pixel space. Although convolutional networks would seem appropriate for this task, we show that they fail spectacularly. We demonstrate and carefully analyze the failure first on a toy problem, at which point a simple fix becomes obvious. We call this solution CoordConv, which works by giving convolution access to its own input coordinates through the use of extra coordinate channels. Without sacrificing the computational and parametric efficiency of ordinary convolution, CoordConv allows networks to learn either perfect translation invariance or varying degrees of translation dependence, as required by the task. CoordConv solves the coordinate transform problem with perfect generalization and 150 times faster with 10--100 times fewer parameters than convolution. This stark contrast raises the question: to what extent has this inability of convolution persisted insidiously inside other tasks, subtly hampering performance from within? A complete answer to this question will require further investigation, but we show preliminary evidence that swapping convolution for CoordConv can improve models on a diverse set of tasks. Using CoordConv in a GAN produced less mode collapse as the transform between high-level spatial latents and pixels becomes easier to learn. A Faster R-CNN detection model trained on MNIST detection showed 24% better IOU when using CoordConv, and in the RL domain agents playing Atari games benefit significantly from the use of CoordConv layers.