Identification of Bivariate Causal Directionality Based on Anticipated Asymmetric Geometries

Identification of causal directionality in bivariate numerical data is a fundamental research problem with important practical implications. This paper presents two alternative methods to identify direction of causation by considering conditional distributions: (1) Anticipated Asymmetric Geometries (AAG) and (2) Monotonicity Index. The AAG method compares the actual conditional distributions to anticipated ones along two variables. Different comparison metrics, such as correlation, cosine similarity, Jaccard index, K-L divergence, K-S distance, and mutual information have been evaluated. Anticipated distributions have been projected as normal based on dual response statistics: mean and standard deviation. The Monotonicity Index approach compares the calculated monotonicity indexes of the gradients of conditional distributions along two axes and exhibits counts of gradient sign changes. Both methods assume stochastic properties of the bivariate data and exploit anticipated unimodality of conditional distributions of the effect. It turns out that the tuned AAG method outperforms the Monotonicity Index and reaches a top accuracy of 77.9% compared to ANMs accuracy of 63 +/- 10% when classifying 95 pairs of real-world examples (Mooij et al, 2014). The described methods include a number of hyperparameters that impact accuracy of the identification. For a given set of hyperparameters, both the AAG or Monotonicity Index method provide a unique deterministic outcome of the solution. To address sensitivity to hyperparameters, tuning of hyperparameters has been done by utilizing a full factorial Design of Experiment. A decision tree has been fitted to distinguish misclassified cases using the input data's symmetrical bivariate statistics to address the question of: How decisive is the identification method of causal directionality?

Alternatives of Unsupervised Representations of Variables on the Latent Space

The article addresses the application of unsupervised machine learning to represent variables on the 2D latent space by applying a variational autoencoder (beta-VAE). Representation of variables on low dimensional spaces allows for data visualization, disentanglement of variables based on underlying characteristics, finding of meaningful patterns and outliers, and supports interpretability. Five distinct methods have been introduced to represent variables on the latent space: (1) straightforward transposed, (2) univariate metadata of variables, such as variable statistics, empirical probability density and cumulative distribution functions, (3) adjacency matrices of different metrics, such as correlations, R2 values, Jaccard index, cosine similarity, and mutual information, (4) gradient mappings followed by spot cross product calculation, and (5) combined. Twenty-eight approaches of variable representations by beta-VAE have been considered. The pairwise spot cross product addresses relationships of gradients of two variables along latent space axes, such as orthogonal, confounded positive, confounded negative, and everything in between. The article addresses generalized representations of variables that cover both features and labels. Dealing with categorical variables, reinforced entanglement has been introduced to represent one-hot encoded categories. The article includes three examples: (1) synthetic data with known dependencies, (2) famous MNIST example of handwritten numbers, and (3) real-world multivariate time series of Canadian financial market interest rates. As a result, unsupervised representations of interest rates on the latent space correctly disentangled rates based on their type, such as bonds, T-bills, GICs, or conventional mortgages, positioned bonds and T-bills along a single curve, and ordered rates by their terms along that curve.

Time Series of Non-Additive Metrics: Identification and Interpretation of Contributing Factors of Variance by Linear Decomposition

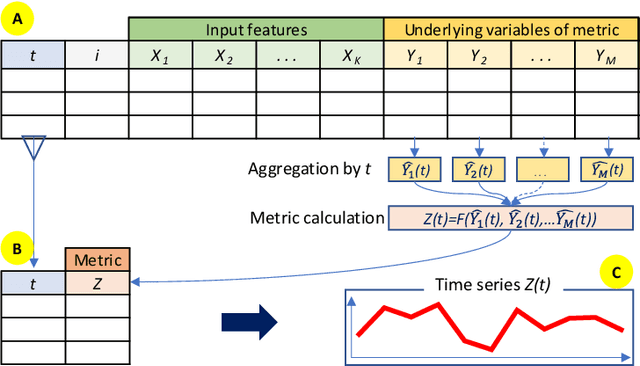
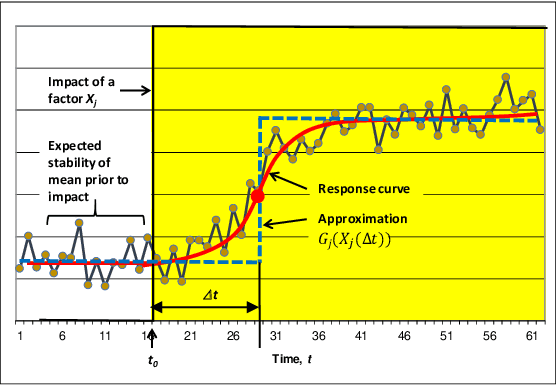
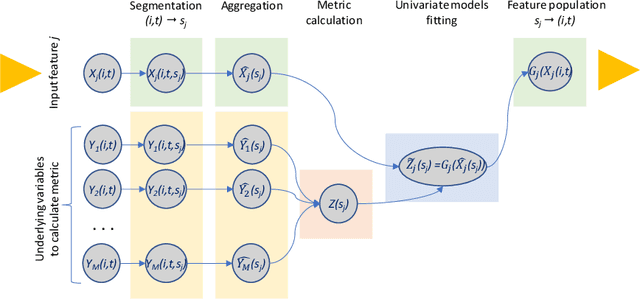
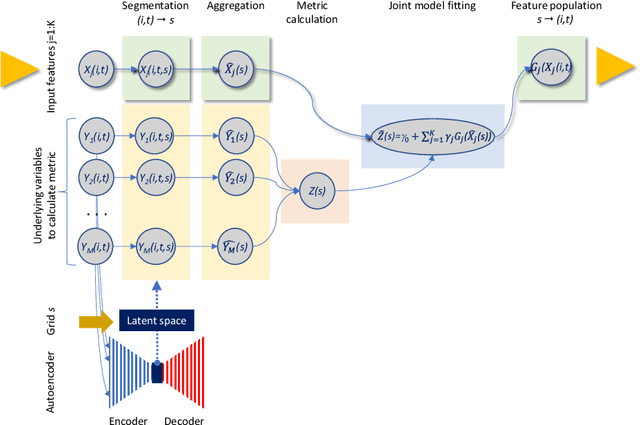
The research paper addresses linear decomposition of time series of non-additive metrics that allows for the identification and interpretation of contributing factors (input features) of variance. Non-additive metrics, such as ratios, are widely used in a variety of domains. It commonly requires preceding aggregations of underlying variables that are used to calculate the metric of interest. The latest poses a dimensionality challenge when the input features and underlying variables are formed as two-dimensional arrays along elements, such as account or customer identifications, and time points. It rules out direct modeling of the time series of a non-additive metric as a function of input features. The article discusses a five-step approach: (1) segmentations of input features and the underlying variables of the metric that are supported by unsupervised autoencoders, (2) univariate or joint fittings of the metric by the aggregated input features on the segmented domains, (3) transformations of pre-screened input features according to the fitted models, (4) aggregation of the transformed features as time series, and (5) modelling of the metric time series as a sum of constrained linear effects of the aggregated features. Alternatively, approximation by numerical differentiation has been considered to linearize the metric. It allows for element level univariate or joint modeling of step (2). The process of these analytical steps allows for a backward-looking explanatory decomposition of the metric as a sum of time series of the survived input features. The paper includes a synthetic example that studies loss-to-balance monthly rates of a hypothetical retail credit portfolio. To validate that no latent factors other than the survived input features have significant impacts on the metric, Statistical Process Control has been introduced for the residual time series.

Designing Complex Experiments by Applying Unsupervised Machine Learning

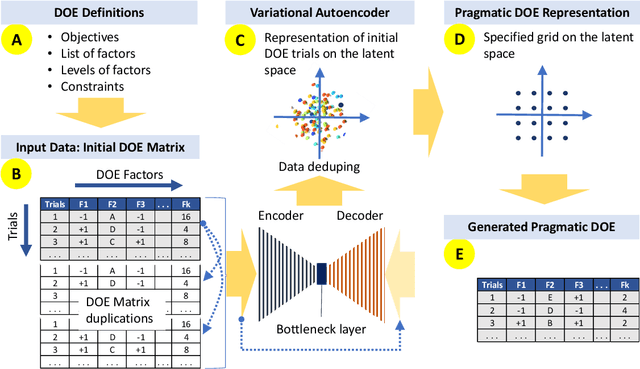
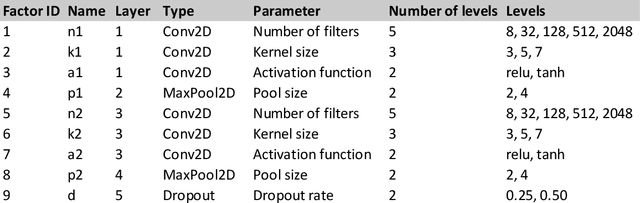
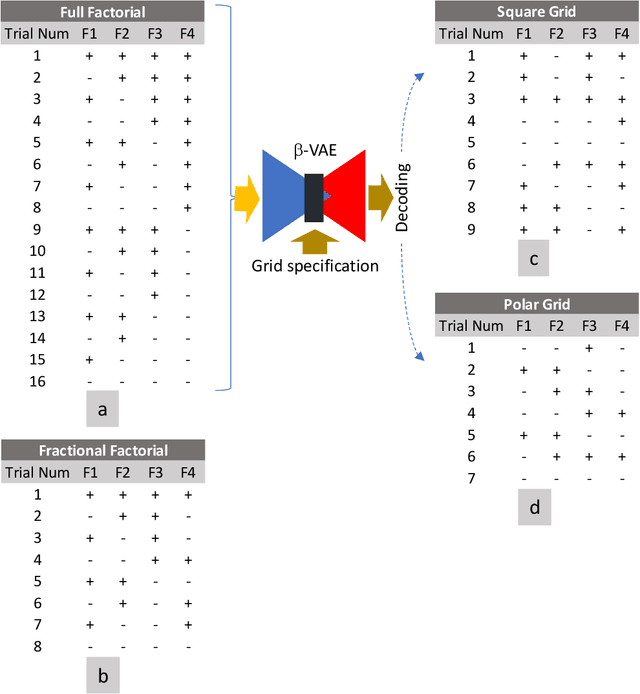
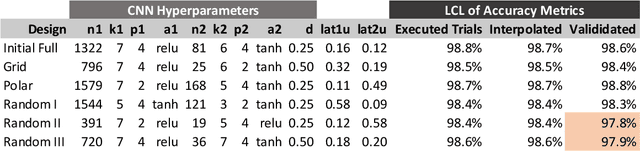
Design of experiments (DOE) is playing an essential role in learning and improving a variety of objects and processes. The article discusses the application of unsupervised machine learning to support the pragmatic designs of complex experiments. Complex experiments are characterized by having a large number of factors, mixed-level designs, and may be subject to constraints that eliminate some unfeasible trials for various reasons. Having such attributes, it is very challenging to design pragmatic experiments that are economically, operationally, and timely sound. It means a significant decrease in the number of required trials from a full factorial design, while still attempting to achieve the defined objectives. A beta variational autoencoder (beta-VAE) has been applied to represent trials of the initial full factorial design after filtering out unfeasible trials on the low dimensional latent space. Regarding visualization and interpretability, the paper is limited to 2D representations. Beta-VAE supports (1) orthogonality of the latent space dimensions, (2) isotropic multivariate standard normal distribution of the representation on the latent space, (3) disentanglement of the latent space representation by levels of factors, (4) propagation of the applied constraints of the initial design into the latent space, and (5) generation of trials by decoding latent space points. Having an initial design representation on the latent space with such properties, it allows for the generation of pragmatic design of experiments (G-DOE) by specifying the number of trials and their pattern on the latent space, such as square or polar grids. Clustering and aggregated gradient metrics have been shown to guide grid specification.

AI Discovering a Coordinate System of Chemical Elements: Dual Representation by Variational Autoencoders

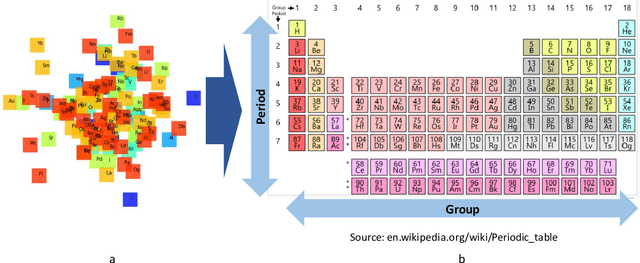
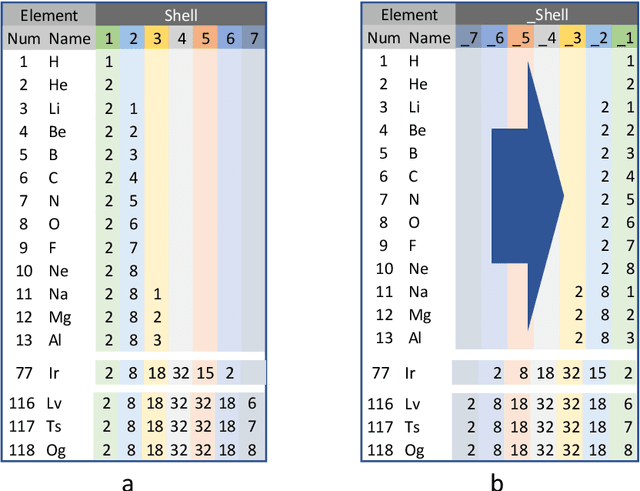
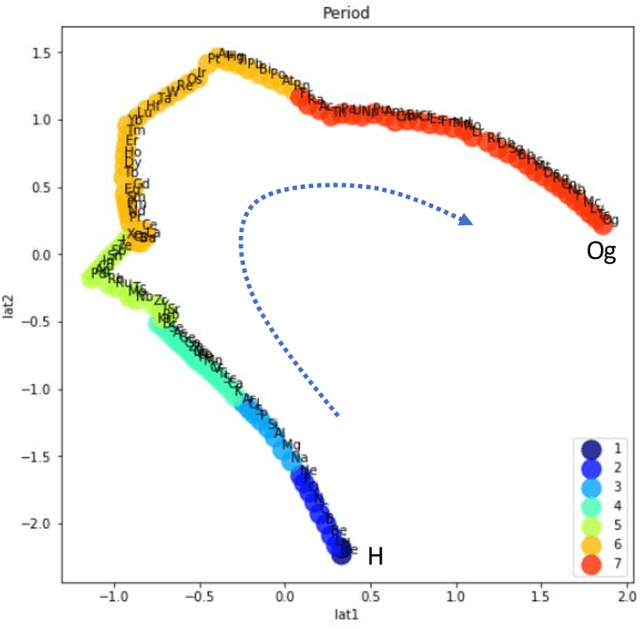
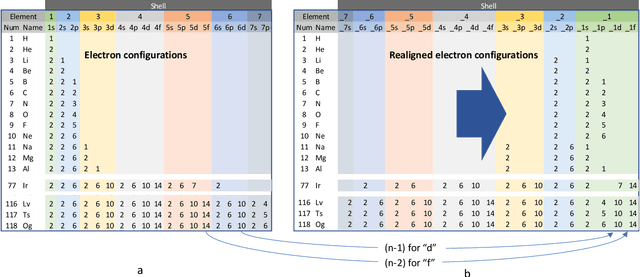
The periodic table is a fundamental representation of chemical elements that plays essential theoretical and practical roles. The research article discusses the experiences of unsupervised training of neural networks to represent elements on the 2D latent space based on their electron configurations while forcing disentanglement. To emphasize chemical properties of the elements, the original data of electron configurations has been realigned towards the outermost valence orbitals. Recognizing seven shells and four subshells, the input data has been arranged as (7x4) images. Latent space representation has been performed using a convolutional beta variational autoencoder (beta-VAE). Despite discrete and sparse input data, the beta-VAE disentangles elements of different periods, blocks, groups, and types, while retaining the order along atomic numbers. In addition, it isolates outliers on the latent space that turned out to be known cases of Madelung's rule violations for lanthanide and actinide elements. Considering the generative capabilities of beta-VAE and discrete input data, the supervised machine learning has been set to find out if there are insightful patterns distinguishing electron configurations between real elements and decoded artificial ones. Also, the article addresses the capability of dual representation by autoencoders. Conventionally, autoencoders represent observations of input data on the latent space. However, by transposing and duplicating original input data, it is possible to represent variables on the latent space as well. The latest can lead to the discovery of meaningful patterns among input variables. Applying that unsupervised learning for transposed data of electron configurations, the order of input variables that has been arranged by the encoder on the latent space has turned out to exactly match the sequence of Madelung's rule.

AI Giving Back to Statistics? Discovery of the Coordinate System of Univariate Distributions by Beta Variational Autoencoder

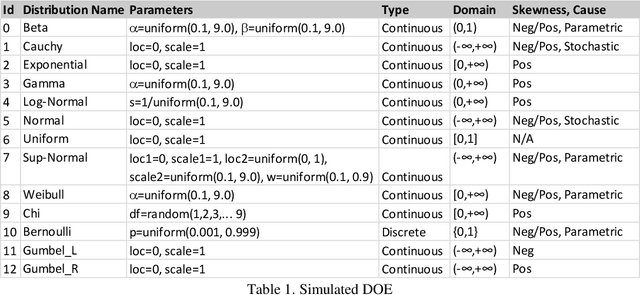
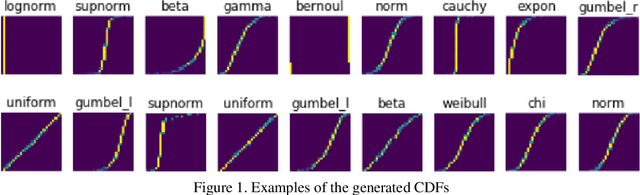
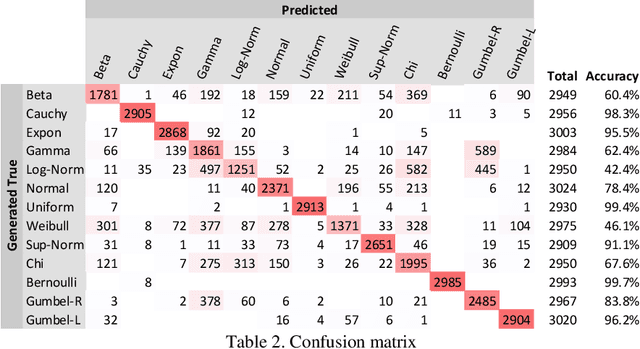
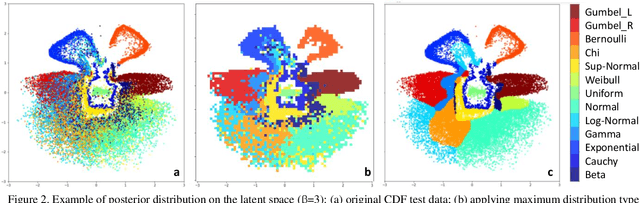
Distributions are fundamental statistical elements that play essential theoretical and practical roles. The article discusses experiences of training neural networks to classify univariate empirical distributions and to represent them on the two-dimensional latent space forcing disentanglement based on the inputs of cumulative distribution functions (CDF). The latent space representation has been performed using an unsupervised beta variational autoencoder (beta-VAE). It separates distributions of different shapes while overlapping similar ones and empirically realises relationships between distributions that are known theoretically. The synthetic experiment of generated univariate continuous and discrete (Bernoulli) distributions with varying sample sizes and parameters has been performed to support the study. The representation on the latent two-dimensional coordinate system can be seen as an additional metadata of the real-world data that disentangles important distribution characteristics, such as shape of the CDF, classification probabilities of underlying theoretical distributions and their parameters, information entropy, and skewness. Entropy changes, providing an "arrow of time", determine dynamic trajectories along representations of distributions on the latent space. In addition, post beta-VAE unsupervised segmentation of the latent space based on weight-of-evidence (WOE) of posterior versus standard isotopic two-dimensional normal densities has been applied detecting the presence of assignable causes that distinguish exceptional CDF inputs.