Machine Learning for Smart and Energy-Efficient Buildings

Energy consumption in buildings, both residential and commercial, accounts for approximately 40% of all energy usage in the U.S., and similar numbers are being reported from countries around the world. This significant amount of energy is used to maintain a comfortable, secure, and productive environment for the occupants. So, it is crucial that the energy consumption in buildings must be optimized, all the while maintaining satisfactory levels of occupant comfort, health, and safety. Recently, Machine Learning has been proven to be an invaluable tool in deriving important insights from data and optimizing various systems. In this work, we review the ways in which machine learning has been leveraged to make buildings smart and energy-efficient. For the convenience of readers, we provide a brief introduction of several machine learning paradigms and the components and functioning of each smart building system we cover. Finally, we discuss challenges faced while implementing machine learning algorithms in smart buildings and provide future avenues for research at the intersection of smart buildings and machine learning.

Data-Driven Reachability analysis and Support set Estimation with Christoffel Functions

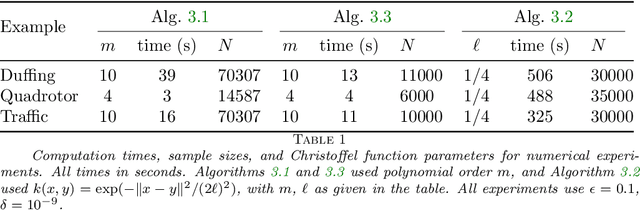
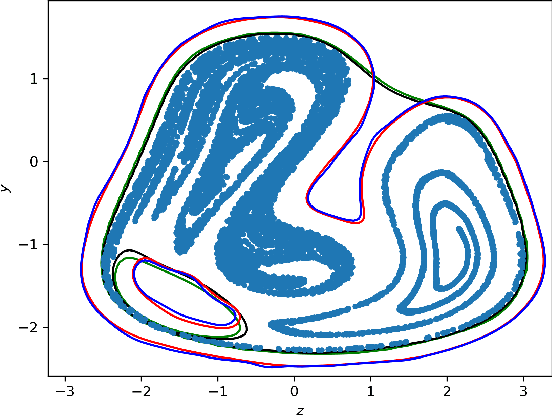
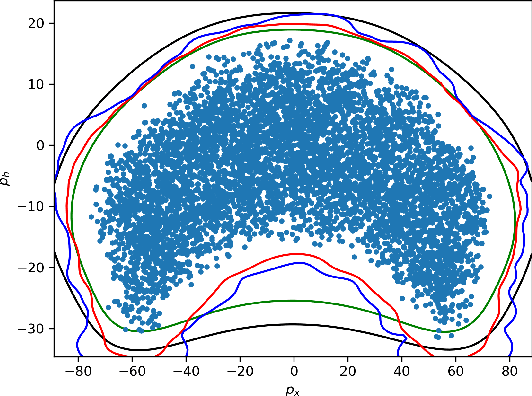
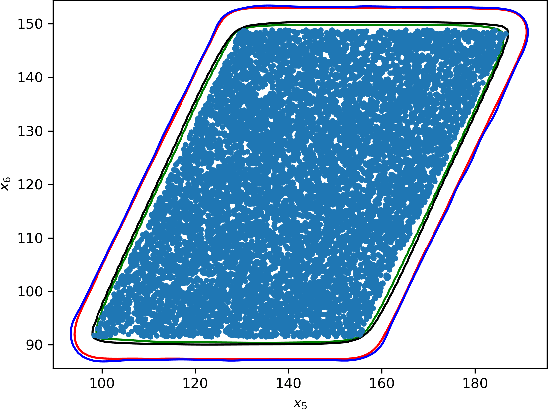
We present algorithms for estimating the forward reachable set of a dynamical system using only a finite collection of independent and identically distributed samples. The produced estimate is the sublevel set of a function called an empirical inverse Christoffel function: empirical inverse Christoffel functions are known to provide good approximations to the support of probability distributions. In addition to reachability analysis, the same approach can be applied to general problems of estimating the support of a random variable, which has applications in data science towards detection of novelties and outliers in data sets. In applications where safety is a concern, having a guarantee of accuracy that holds on finite data sets is critical. In this paper, we prove such bounds for our algorithms under the Probably Approximately Correct (PAC) framework. In addition to applying classical Vapnik-Chervonenkis (VC) dimension bound arguments, we apply the PAC-Bayes theorem by leveraging a formal connection between kernelized empirical inverse Christoffel functions and Gaussian process regression models. The bound based on PAC-Bayes applies to a more general class of Christoffel functions than the VC dimension argument, and achieves greater sample efficiency in experiments.

Symbolic Abstractions From Data: A PAC Learning Approach

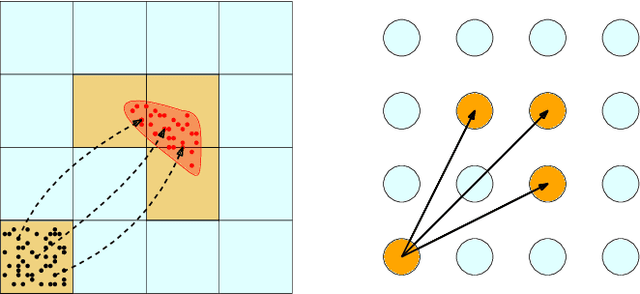
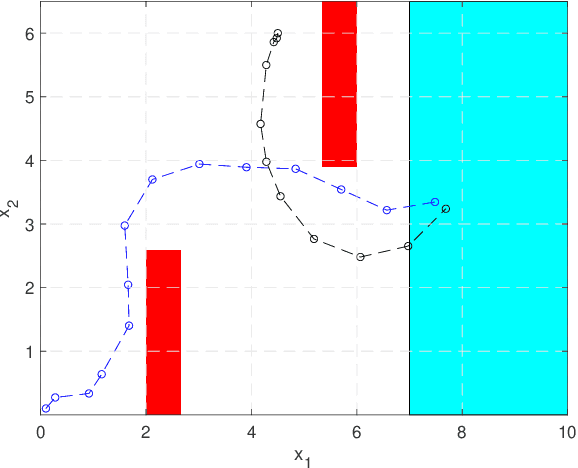
Symbolic control techniques aim to satisfy complex logic specifications. A critical step in these techniques is the construction of a symbolic (discrete) abstraction, a finite-state system whose behaviour mimics that of a given continuous-state system. The methods used to compute symbolic abstractions, however, require knowledge of an accurate closed-form model. To generalize them to systems with unknown dynamics, we present a new data-driven approach that does not require closed-form dynamics, instead relying only the ability to evaluate successors of each state under given inputs. To provide guarantees for the learned abstraction, we use the Probably Approximately Correct (PAC) statistical framework. We first introduce a PAC-style behavioural relationship and an appropriate refinement procedure. We then show how the symbolic abstraction can be constructed to satisfy this new behavioural relationship. Moreover, we provide PAC bounds that dictate the number of data required to guarantee a prescribed level of accuracy and confidence. Finally, we present an illustrative example.