Compressing Deep ODE-Nets using Basis Function Expansions

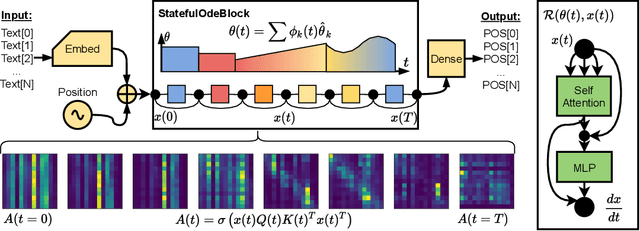
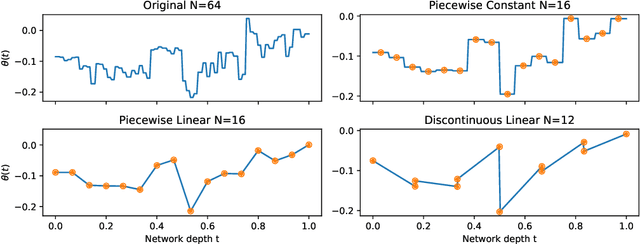
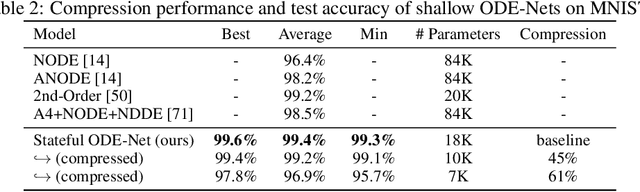
The recently-introduced class of ordinary differential equation networks (ODE-Nets) establishes a fruitful connection between deep learning and dynamical systems. In this work, we reconsider formulations of the weights as continuous-depth functions using linear combinations of basis functions. This perspective allows us to compress the weights through a change of basis, without retraining, while maintaining near state-of-the-art performance. In turn, both inference time and the memory footprint are reduced, enabling quick and rigorous adaptation between computational environments. Furthermore, our framework enables meaningful continuous-in-time batch normalization layers using function projections. The performance of basis function compression is demonstrated by applying continuous-depth models to (a) image classification tasks using convolutional units and (b) sentence-tagging tasks using transformer encoder units.

Lipschitz Recurrent Neural Networks

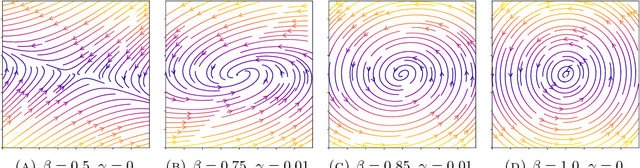
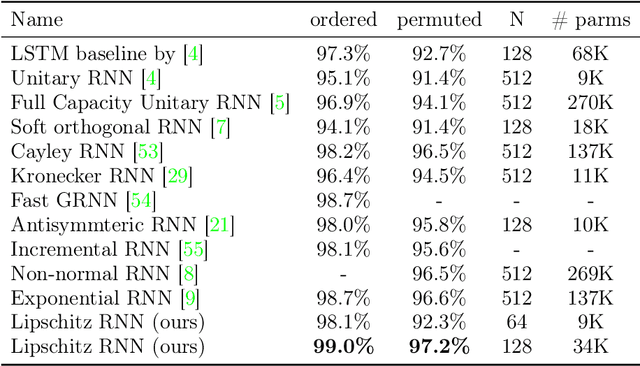
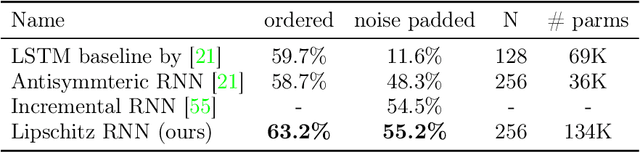
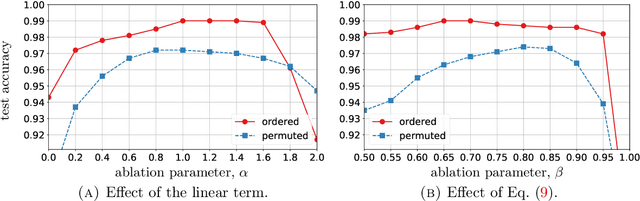
Differential equations are a natural choice for modeling recurrent neural networks because they can be viewed as dynamical systems with a driving input. In this work, we propose a recurrent unit that describes the hidden state's evolution with two parts: a well-understood linear component plus a Lipschitz nonlinearity. This particular functional form simplifies stability analysis, which enables us to provide an asymptotic stability guarantee. Further, we demonstrate that Lipschitz recurrent units are more robust with respect to perturbations. We evaluate our approach on a range of benchmark tasks, and we show it outperforms existing recurrent units.