Akshay Srinivasan
A Multilingual Evaluation of NER Robustness to Adversarial Inputs
May 30, 2023Abstract:Adversarial evaluations of language models typically focus on English alone. In this paper, we performed a multilingual evaluation of Named Entity Recognition (NER) in terms of its robustness to small perturbations in the input. Our results showed the NER models we explored across three languages (English, German and Hindi) are not very robust to such changes, as indicated by the fluctuations in the overall F1 score as well as in a more fine-grained evaluation. With that knowledge, we further explored whether it is possible to improve the existing NER models using a part of the generated adversarial data sets as augmented training data to train a new NER model or as fine-tuning data to adapt an existing NER model. Our results showed that both these approaches improve performance on the original as well as adversarial test sets. While there is no significant difference between the two approaches for English, re-training is significantly better than fine-tuning for German and Hindi.
MA-Dreamer: Coordination and communication through shared imagination
Apr 10, 2022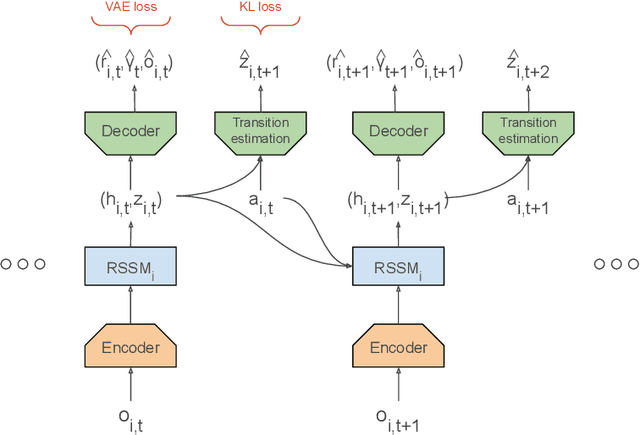

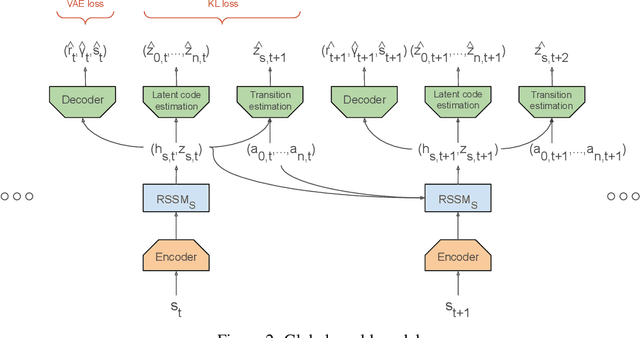

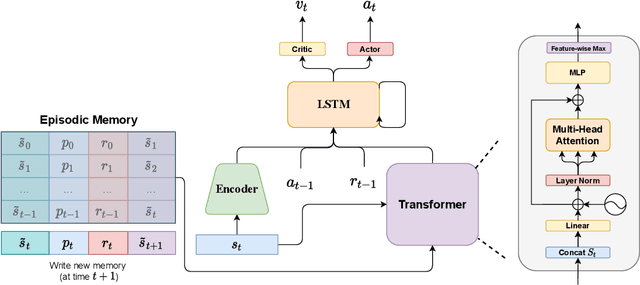
Abstract:Multi-agent RL is rendered difficult due to the non-stationary nature of environment perceived by individual agents. Theoretically sound methods using the REINFORCE estimator are impeded by its high-variance, whereas value-function based methods are affected by issues stemming from their ad-hoc handling of situations like inter-agent communication. Methods like MADDPG are further constrained due to their requirement of centralized critics etc. In order to address these issues, we present MA-Dreamer, a model-based method that uses both agent-centric and global differentiable models of the environment in order to train decentralized agents' policies and critics using model-rollouts a.k.a `imagination'. Since only the model-training is done off-policy, inter-agent communication/coordination and `language emergence' can be handled in a straight-forward manner. We compare the performance of MA-Dreamer with other methods on two soccer-based games. Our experiments show that in long-term speaker-listener tasks and in cooperative games with strong partial-observability, MA-Dreamer finds a solution that makes effective use of coordination, whereas competing methods obtain marginal scores and fail outright, respectively. By effectively achieving coordination and communication under more relaxed and general conditions, out method opens the door to the study of more complex problems and population-based training.
How to Learn and Represent Abstractions: An Investigation using Symbolic Alchemy
Dec 14, 2021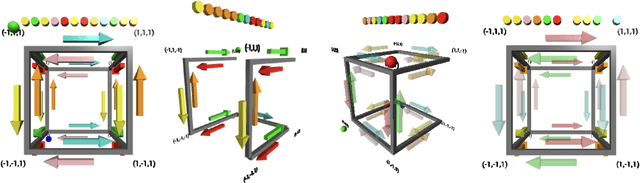
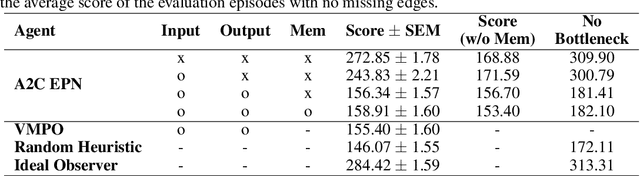
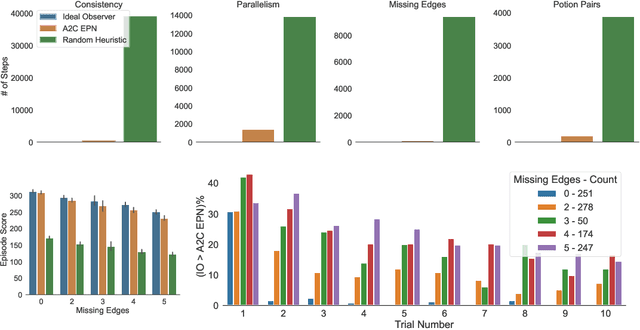
Abstract:Alchemy is a new meta-learning environment rich enough to contain interesting abstractions, yet simple enough to make fine-grained analysis tractable. Further, Alchemy provides an optional symbolic interface that enables meta-RL research without a large compute budget. In this work, we take the first steps toward using Symbolic Alchemy to identify design choices that enable deep-RL agents to learn various types of abstraction. Then, using a variety of behavioral and introspective analyses we investigate how our trained agents use and represent abstract task variables, and find intriguing connections to the neuroscience of abstraction. We conclude by discussing the next steps for using meta-RL and Alchemy to better understand the representation of abstract variables in the brain.
Computing the Newton-step faster than Hessian accumulation
Aug 02, 2021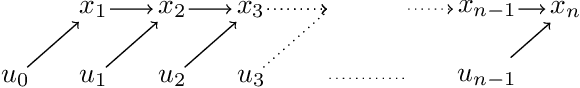

Abstract:Computing the Newton-step of a generic function with $N$ decision variables takes $O(N^3)$ flops. In this paper, we show that given the computational graph of the function, this bound can be reduced to $O(m\tau^3)$, where $\tau, m$ are the width and size of a tree-decomposition of the graph. The proposed algorithm generalizes nonlinear optimal-control methods based on LQR to general optimization problems and provides non-trivial gains in iteration-complexity even in cases where the Hessian is dense.
Graphical Newton
Oct 08, 2017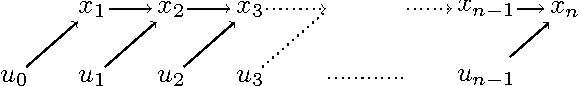
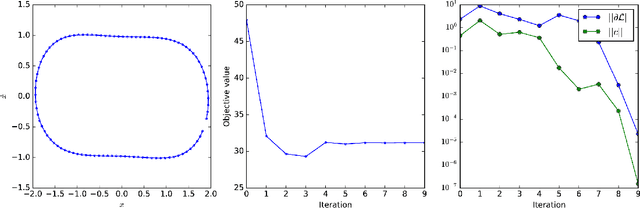
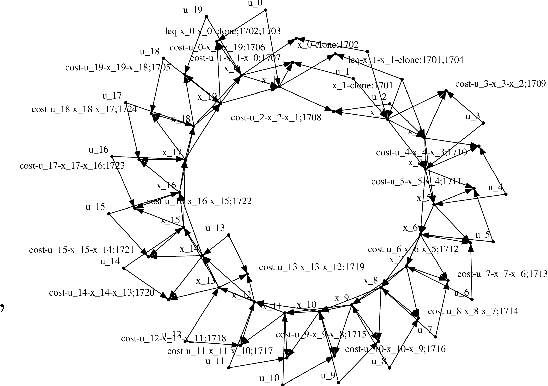
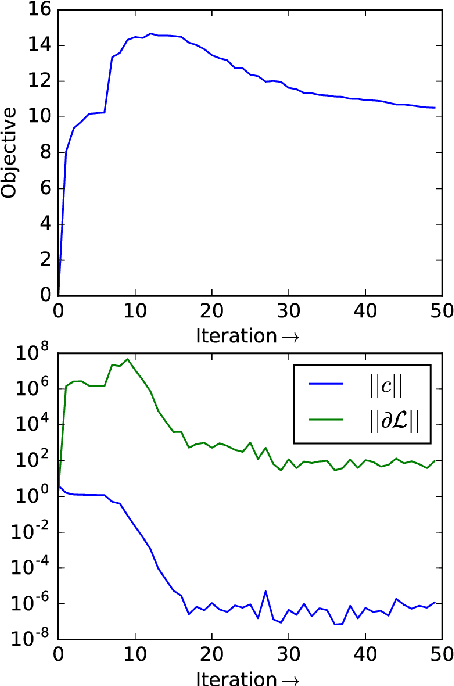
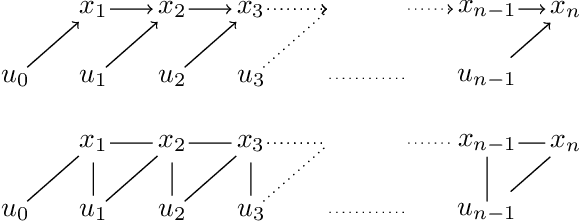
Abstract:Computing the Newton step for a generic function $f: \mathbb{R}^N \rightarrow \mathbb{R}$ takes $O(N^{3})$ flops. In this paper, we explore avenues for reducing this bound, when the computational structure of $f$ is known beforehand. It is shown that the Newton step can be computed in time, linear in the size of the computational-graph, and cubic in its tree-width.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge