Non-Asymptotic Analysis of Data Augmentation for Precision Matrix Estimation

This paper addresses the problem of inverse covariance (also known as precision matrix) estimation in high-dimensional settings. Specifically, we focus on two classes of estimators: linear shrinkage estimators with a target proportional to the identity matrix, and estimators derived from data augmentation (DA). Here, DA refers to the common practice of enriching a dataset with artificial samples--typically generated via a generative model or through random transformations of the original data--prior to model fitting. For both classes of estimators, we derive estimators and provide concentration bounds for their quadratic error. This allows for both method comparison and hyperparameter tuning, such as selecting the optimal proportion of artificial samples. On the technical side, our analysis relies on tools from random matrix theory. We introduce a novel deterministic equivalent for generalized resolvent matrices, accommodating dependent samples with specific structure. We support our theoretical results with numerical experiments.

From point processes to quantum optics and back

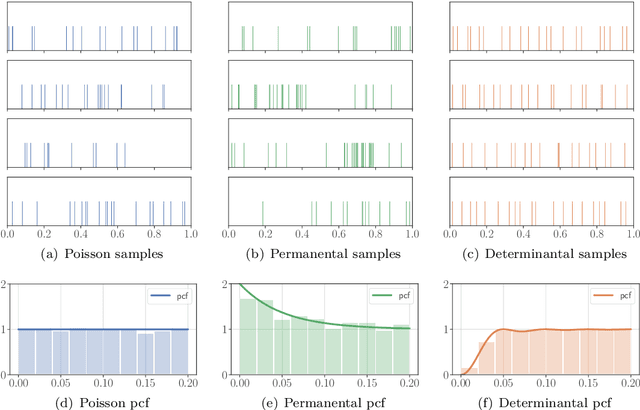
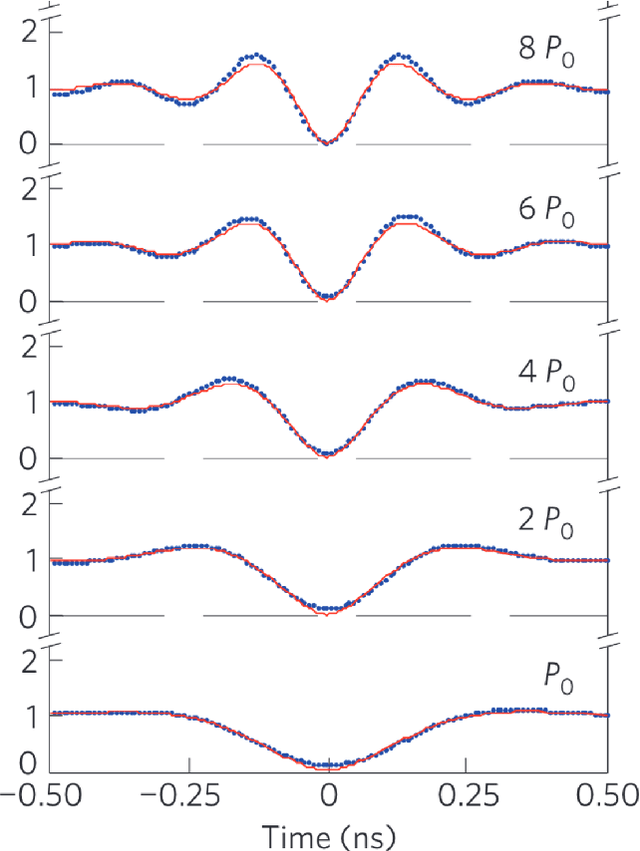
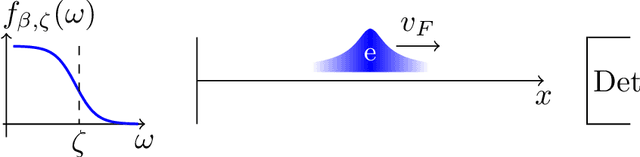
Some fifty years ago, in her seminal PhD thesis, Odile Macchi introduced permanental and determinantal point processes. Her initial motivation was to provide models for the set of detection times in fundamental bosonic or fermionic optical experiments, respectively. After two rather quiet decades, these point processes have quickly become standard examples of point processes with nontrivial, yet tractable, correlation structures. In particular, determinantal point processes have been since the 1990s a technical workhorse in random matrix theory and combinatorics, and a standard model for repulsive point patterns in machine learning and spatial statistics since the 2010s. Meanwhile, our ability to experimentally probe the correlations between detection events in bosonic and fermionic optics has progressed tremendously. In Part I of this survey, we provide a modern introduction to the concepts in Macchi's thesis and their physical motivation, under the combined eye of mathematicians, physicists, and signal processers. Our objective is to provide a shared basis of knowledge for later cross-disciplinary work on point processes in quantum optics, and reconnect with the physical roots of permanental and determinantal point processes.