On Compiling DNNFs without Determinism

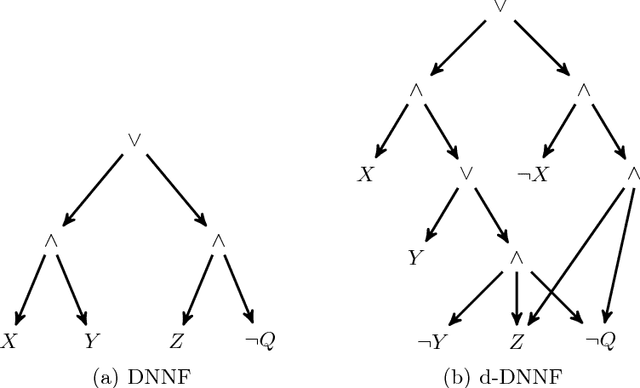
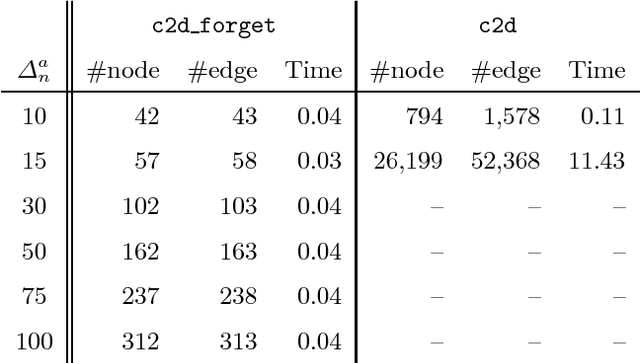
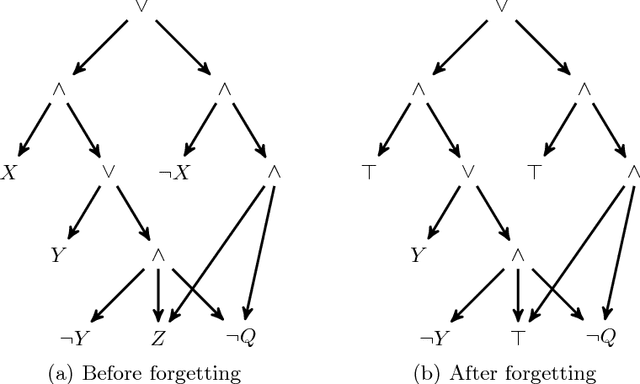
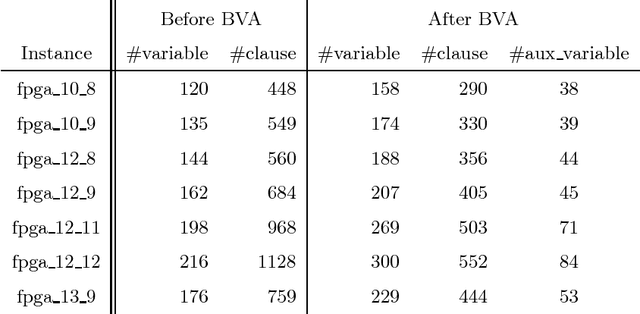
State-of-the-art knowledge compilers generate deterministic subsets of DNNF, which have been recently shown to be exponentially less succinct than DNNF. In this paper, we propose a new method to compile DNNFs without enforcing determinism necessarily. Our approach is based on compiling deterministic DNNFs with the addition of auxiliary variables to the input formula. These variables are then existentially quantified from the deterministic structure in linear time, which would lead to a DNNF that is equivalent to the input formula and not necessarily deterministic. On the theoretical side, we show that the new method could generate exponentially smaller DNNFs than deterministic ones, even by adding a single auxiliary variable. Further, we show that various existing techniques that introduce auxiliary variables to the input formulas can be employed in our framework. On the practical side, we empirically demonstrate that our new method can significantly advance DNNF compilation on certain benchmarks.

On Relaxing Determinism in Arithmetic Circuits

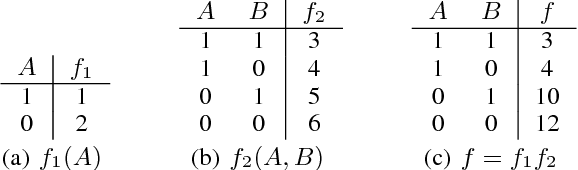
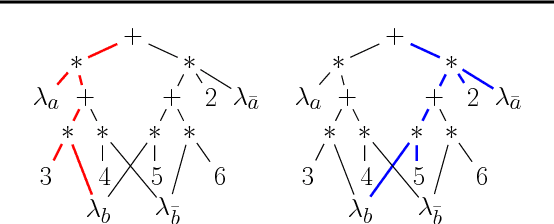
The past decade has seen a significant interest in learning tractable probabilistic representations. Arithmetic circuits (ACs) were among the first proposed tractable representations, with some subsequent representations being instances of ACs with weaker or stronger properties. In this paper, we provide a formal basis under which variants on ACs can be compared, and where the precise roles and semantics of their various properties can be made more transparent. This allows us to place some recent developments on ACs in a clearer perspective and to also derive new results for ACs. This includes an exponential separation between ACs with and without determinism; completeness and incompleteness results; and tractability results (or lack thereof) when computing most probable explanations (MPEs).

Human-Level Intelligence or Animal-Like Abilities?

The vision systems of the eagle and the snake outperform everything that we can make in the laboratory, but snakes and eagles cannot build an eyeglass or a telescope or a microscope. (Judea Pearl)

Dual Decomposition from the Perspective of Relax, Compensate and then Recover

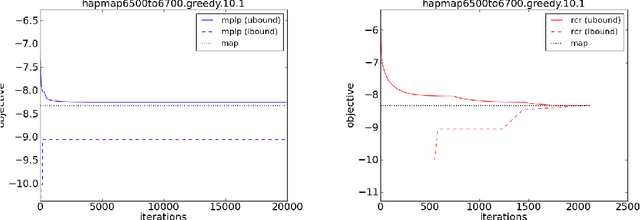
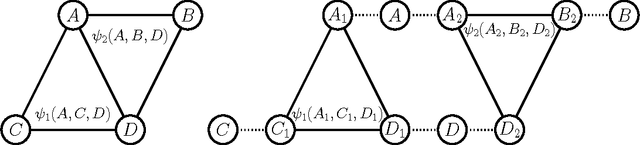
Relax, Compensate and then Recover (RCR) is a paradigm for approximate inference in probabilistic graphical models that has previously provided theoretical and practical insights on iterative belief propagation and some of its generalizations. In this paper, we characterize the technique of dual decomposition in the terms of RCR, viewing it as a specific way to compensate for relaxed equivalence constraints. Among other insights gathered from this perspective, we propose novel heuristics for recovering relaxed equivalence constraints with the goal of incrementally tightening dual decomposition approximations, all the way to reaching exact solutions. We also show empirically that recovering equivalence constraints can sometimes tighten the corresponding approximation (and obtaining exact results), without increasing much the complexity of inference.

Proceedings of the Eighteenth Conference on Uncertainty in Artificial Intelligence (2002)

This is the Proceedings of the Eighteenth Conference on Uncertainty in Artificial Intelligence, which was held in Alberta, Canada, August 1-4 2002

When do Numbers Really Matter?

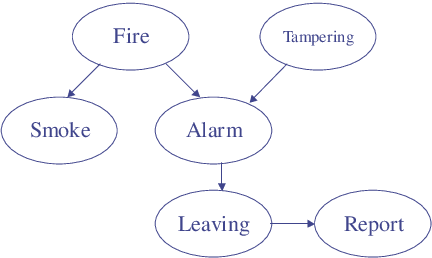
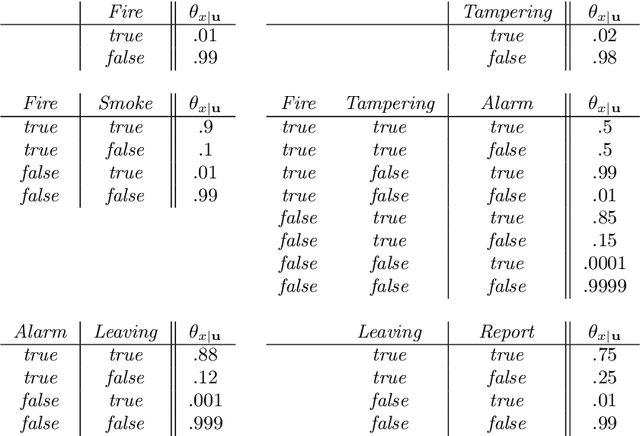
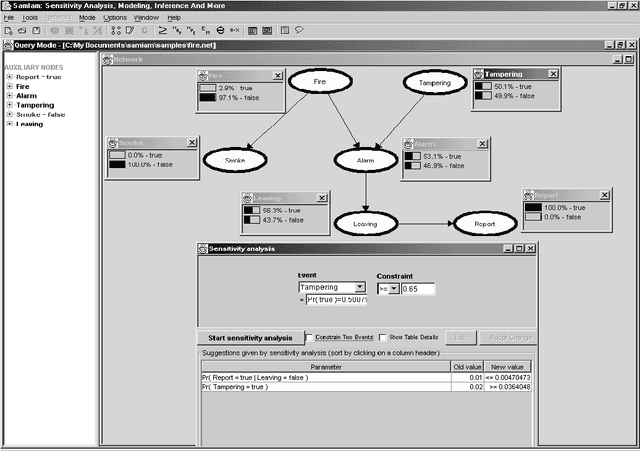
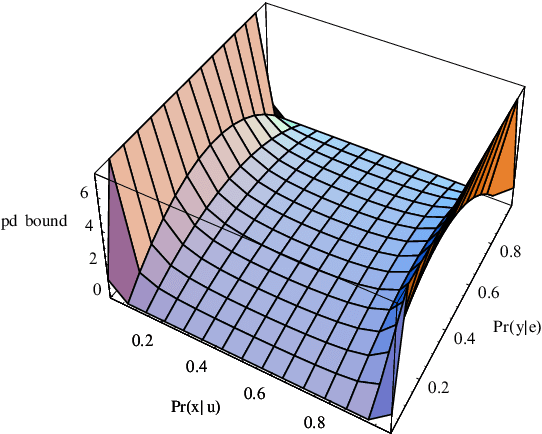
Common wisdom has it that small distinctions in the probabilities quantifying a Bayesian network do not matter much for the resultsof probabilistic queries. However, one can easily develop realistic scenarios under which small variations in network probabilities can lead to significant changes in computed queries. A pending theoretical question is then to analytically characterize parameter changes that do or do not matter. In this paper, we study the sensitivity of probabilistic queries to changes in network parameters and prove some tight bounds on the impact that such parameters can have on queries. Our analytical results pinpoint some interesting situations under which parameter changes do or do not matter. These results are important for knowledge engineers as they help them identify influential network parameters. They are also important for approximate inference algorithms that preprocessnetwork CPTs to eliminate small distinctions in probabilities.

Query DAGs: A Practical Paradigm for Implementing Belief Network Inference

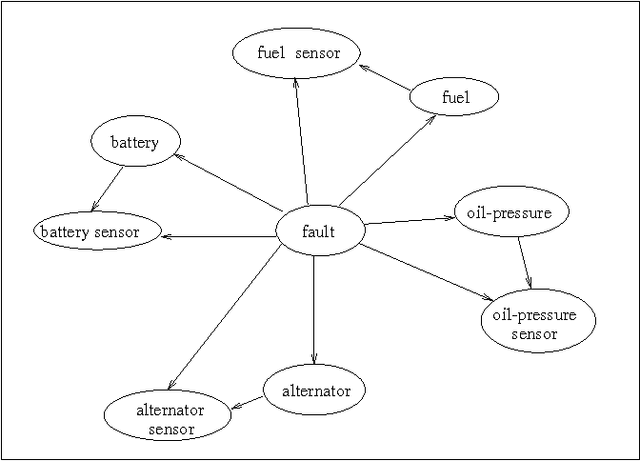
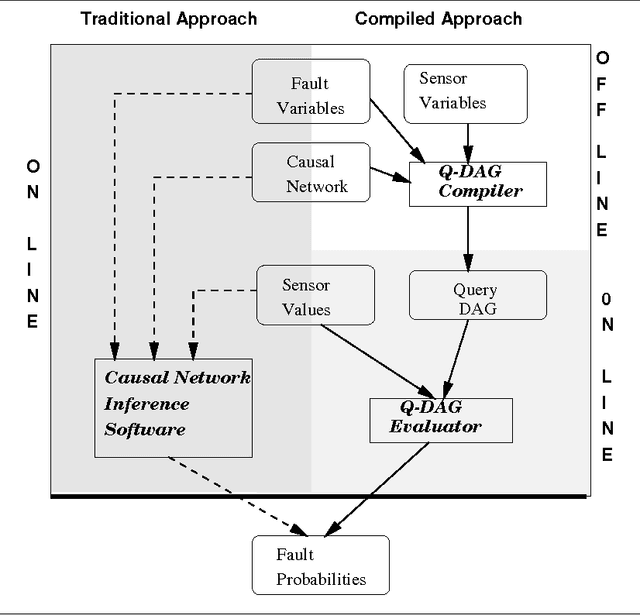
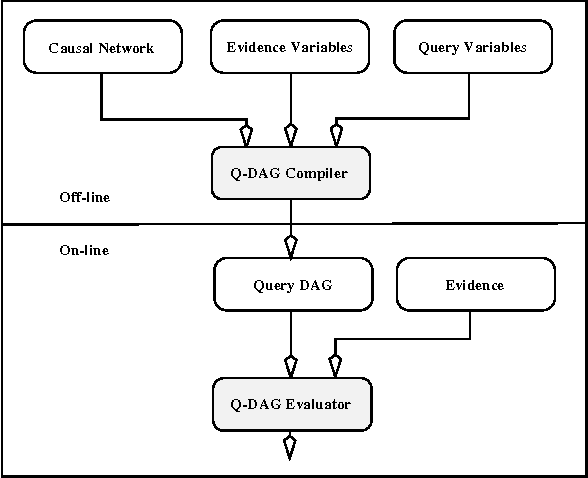
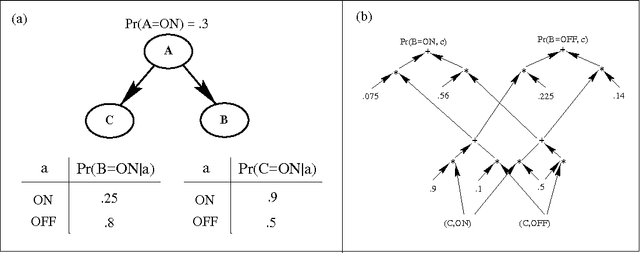
We describe a new paradigm for implementing inference in belief networks, which relies on compiling a belief network into an arithmetic expression called a Query DAG (Q-DAG). Each non-leaf node of a Q-DAG represents a numeric operation, a number, or a symbol for evidence. Each leaf node of a Q-DAG represents the answer to a network query, that is, the probability of some event of interest. It appears that Q-DAGs can be generated using any of the algorithms for exact inference in belief networks --- we show how they can be generated using clustering and conditioning algorithms. The time and space complexity of a Q-DAG generation algorithm is no worse than the time complexity of the inference algorithm on which it is based; that of a Q-DAG on-line evaluation algorithm is linear in the size of the Q-DAG, and such inference amounts to a standard evaluation of the arithmetic expression it represents. The main value of Q-DAGs is in reducing the software and hardware resources required to utilize belief networks in on-line, real-world applications. The proposed framework also facilitates the development of on-line inference on different software and hardware platforms, given the simplicity of the Q-DAG evaluation algorithm. This paper describes this new paradigm for probabilistic inference, explaining how it works, its uses, and outlines some of the research directions that it leads to.

On the Role of Canonicity in Bottom-up Knowledge Compilation

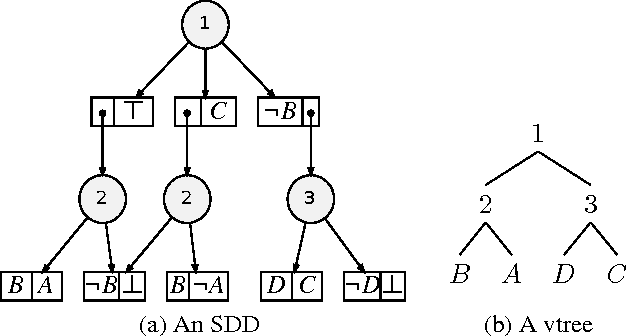
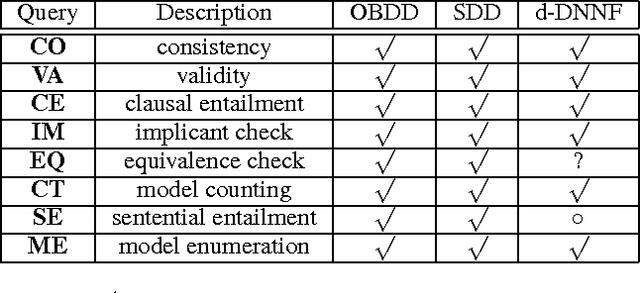
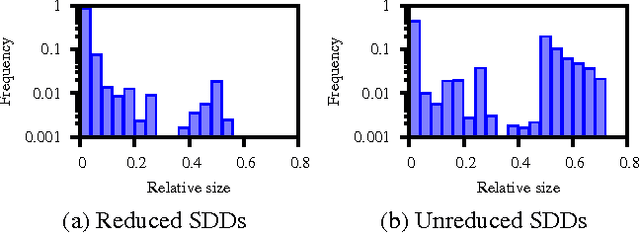
We consider the problem of bottom-up compilation of knowledge bases, which is usually predicated on the existence of a polytime function for combining compilations using Boolean operators (usually called an Apply function). While such a polytime Apply function is known to exist for certain languages (e.g., OBDDs) and not exist for others (e.g., DNNF), its existence for certain languages remains unknown. Among the latter is the recently introduced language of Sentential Decision Diagrams (SDDs), for which a polytime Apply function exists for unreduced SDDs, but remains unknown for reduced ones (i.e. canonical SDDs). We resolve this open question in this paper and consider some of its theoretical and practical implications. Some of the findings we report question the common wisdom on the relationship between bottom-up compilation, language canonicity and the complexity of the Apply function.

Skolemization for Weighted First-Order Model Counting

First-order model counting emerged recently as a novel reasoning task, at the core of efficient algorithms for probabilistic logics. We present a Skolemization algorithm for model counting problems that eliminates existential quantifiers from a first-order logic theory without changing its weighted model count. For certain subsets of first-order logic, lifted model counters were shown to run in time polynomial in the number of objects in the domain of discourse, where propositional model counters require exponential time. However, these guarantees apply only to Skolem normal form theories (i.e., no existential quantifiers) as the presence of existential quantifiers reduces lifted model counters to propositional ones. Since textbook Skolemization is not sound for model counting, these restrictions precluded efficient model counting for directed models, such as probabilistic logic programs, which rely on existential quantification. Our Skolemization procedure extends the applicability of first-order model counters to these representations. Moreover, it simplifies the design of lifted model counting algorithms.

On the Complexity and Approximation of Binary Evidence in Lifted Inference

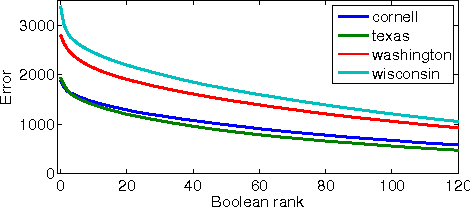
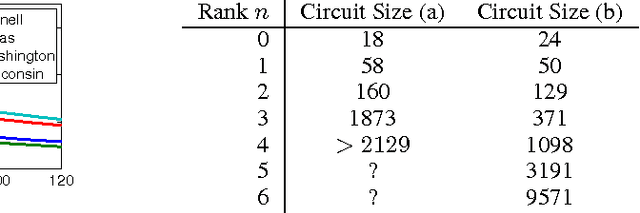
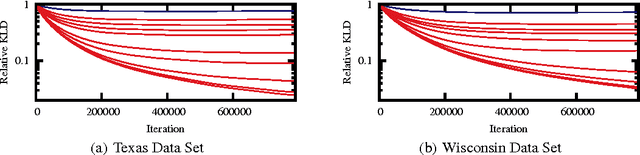
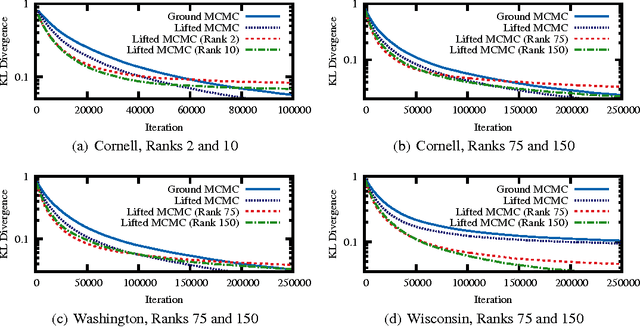
Lifted inference algorithms exploit symmetries in probabilistic models to speed up inference. They show impressive performance when calculating unconditional probabilities in relational models, but often resort to non-lifted inference when computing conditional probabilities. The reason is that conditioning on evidence breaks many of the model's symmetries, which can preempt standard lifting techniques. Recent theoretical results show, for example, that conditioning on evidence which corresponds to binary relations is #P-hard, suggesting that no lifting is to be expected in the worst case. In this paper, we balance this negative result by identifying the Boolean rank of the evidence as a key parameter for characterizing the complexity of conditioning in lifted inference. In particular, we show that conditioning on binary evidence with bounded Boolean rank is efficient. This opens up the possibility of approximating evidence by a low-rank Boolean matrix factorization, which we investigate both theoretically and empirically.