A Dataless Reinforcement Learning Approach to Rounding Hyperplane Optimization for Max-Cut

The Maximum Cut (MaxCut) problem is NP-Complete, and obtaining its optimal solution is NP-hard in the worst case. As a result, heuristic-based algorithms are commonly used, though their design often requires significant domain expertise. More recently, learning-based methods trained on large (un)labeled datasets have been proposed; however, these approaches often struggle with generalizability and scalability. A well-known approximation algorithm for MaxCut is the Goemans-Williamson (GW) algorithm, which relaxes the Quadratic Unconstrained Binary Optimization (QUBO) formulation into a semidefinite program (SDP). The GW algorithm then applies hyperplane rounding by uniformly sampling a random hyperplane to convert the SDP solution into binary node assignments. In this paper, we propose a training-data-free approach based on a non-episodic reinforcement learning formulation, in which an agent learns to select improved rounding hyperplanes that yield better cuts than those produced by the GW algorithm. By optimizing over a Markov Decision Process (MDP), our method consistently achieves better cuts across large-scale graphs with varying densities and degree distributions.

Automated Selection of Uniform Regions for CT Image Quality Detection

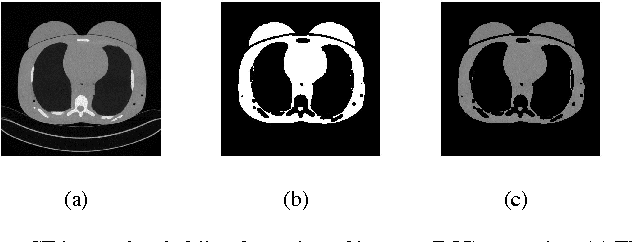
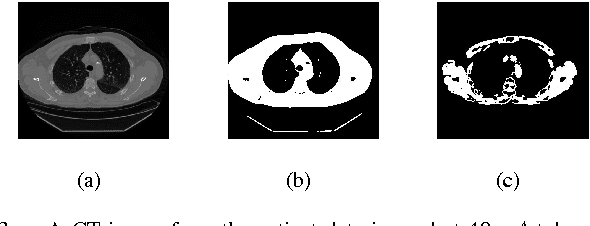
CT images are widely used in pathology detection and follow-up treatment procedures. Accurate identification of pathological features requires diagnostic quality CT images with minimal noise and artifact variation. In this work, a novel Fourier-transform based metric for image quality (IQ) estimation is presented that correlates to additive CT image noise. In the proposed method, two windowed CT image subset regions are analyzed together to identify the extent of variation in the corresponding Fourier-domain spectrum. The two square windows are chosen such that their center pixels coincide and one window is a subset of the other. The Fourier-domain spectral difference between these two sub-sampled windows is then used to isolate spatial regions-of-interest (ROI) with low signal variation (ROI-LV) and high signal variation (ROI-HV), respectively. Finally, the spatial variance ($var$), standard deviation ($std$), coefficient of variance ($cov$) and the fraction of abdominal ROI pixels in ROI-LV ($\nu'(q)$), are analyzed with respect to CT image noise. For the phantom CT images, $var$ and $std$ correlate to CT image noise ($|r|>0.76$ ($p\ll0.001$)), though not as well as $\nu'(q)$ ($r=0.96$ ($p\ll0.001$)). However, for the combined phantom and patient CT images, $var$ and $std$ do not correlate well with CT image noise ($|r|<0.46$ ($p\ll0.001$)) as compared to $\nu'(q)$ ($r=0.95$ ($p\ll0.001$)). Thus, the proposed method and the metric, $\nu'(q)$, can be useful to quantitatively estimate CT image noise.