VARSHAP: Addressing Global Dependency Problems in Explainable AI with Variance-Based Local Feature Attribution

Existing feature attribution methods like SHAP often suffer from global dependence, failing to capture true local model behavior. This paper introduces VARSHAP, a novel model-agnostic local feature attribution method which uses the reduction of prediction variance as the key importance metric of features. Building upon Shapley value framework, VARSHAP satisfies the key Shapley axioms, but, unlike SHAP, is resilient to global data distribution shifts. Experiments on synthetic and real-world datasets demonstrate that VARSHAP outperforms popular methods such as KernelSHAP or LIME, both quantitatively and qualitatively.

Accurate estimation of feature importance faithfulness for tree models

In this paper, we consider a perturbation-based metric of predictive faithfulness of feature rankings (or attributions) that we call PGI squared. When applied to decision tree-based regression models, the metric can be computed accurately and efficiently for arbitrary independent feature perturbation distributions. In particular, the computation does not involve Monte Carlo sampling that has been typically used for computing similar metrics and which is inherently prone to inaccuracies. Moreover, we propose a method of ranking features by their importance for the tree model's predictions based on PGI squared. Our experiments indicate that in some respects, the method may identify the globally important features better than the state-of-the-art SHAP explainer

Improved Feature Importance Computations for Tree Models: Shapley vs. Banzhaf

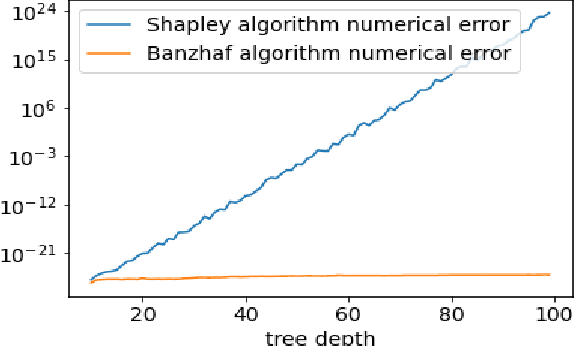
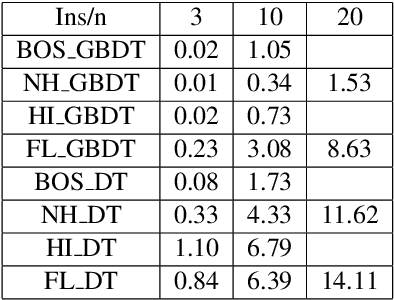
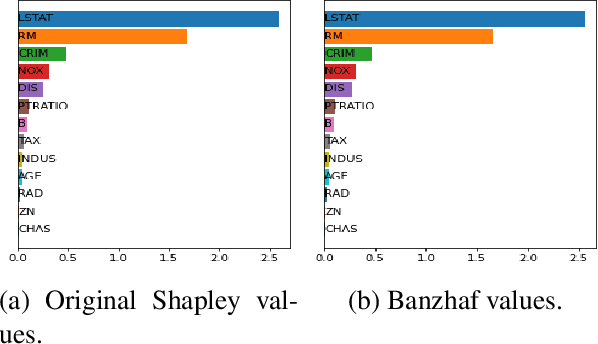
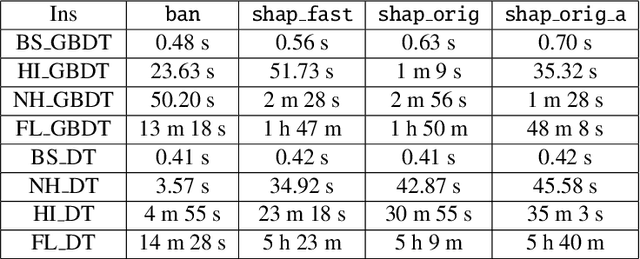
Shapley values are one of the main tools used to explain predictions of tree ensemble models. The main alternative to Shapley values are Banzhaf values that have not been understood equally well. In this paper we make a step towards filling this gap, providing both experimental and theoretical comparison of these model explanation methods. Surprisingly, we show that Banzhaf values offer several advantages over Shapley values while providing essentially the same explanations. We verify that Banzhaf values: (1) have a more intuitive interpretation, (2) allow for more efficient algorithms, and (3) are much more numerically robust. We provide an experimental evaluation of these theses. In particular, we show that on real world instances. Additionally, from a theoretical perspective we provide new and improved algorithm computing the same Shapley value based explanations as the algorithm of Lundberg et al. [Nat. Mach. Intell. 2020]. Our algorithm runs in $O(TLD+n)$ time, whereas the previous algorithm had $O(TLD^2+n)$ running time bound. Here, $T$ is the number of trees, $L$ is the maximum number of leaves in a tree, and $D$ denotes the maximum depth of a tree in the ensemble. Using the computational techniques developed for Shapley values we deliver an optimal $O(TL+n)$ time algorithm for computing Banzhaf values based explanations. In our experiments these algorithms give running times smaller even by an order of magnitude.

Decomposable Submodular Function Minimization via Maximum Flow

This paper bridges discrete and continuous optimization approaches for decomposable submodular function minimization, in both the standard and parametric settings. We provide improved running times for this problem by reducing it to a number of calls to a maximum flow oracle. When each function in the decomposition acts on $O(1)$ elements of the ground set $V$ and is polynomially bounded, our running time is up to polylogarithmic factors equal to that of solving maximum flow in a sparse graph with $O(\vert V \vert)$ vertices and polynomial integral capacities. We achieve this by providing a simple iterative method which can optimize to high precision any convex function defined on the submodular base polytope, provided we can efficiently minimize it on the base polytope corresponding to the cut function of a certain graph that we construct. We solve this minimization problem by lifting the solutions of a parametric cut problem, which we obtain via a new efficient combinatorial reduction to maximum flow. This reduction is of independent interest and implies some previously unknown bounds for the parametric minimum $s,t$-cut problem in multiple settings.