Shannon invariants: A scalable approach to information decomposition

Distributed systems, such as biological and artificial neural networks, process information via complex interactions engaging multiple subsystems, resulting in high-order patterns with distinct properties across scales. Investigating how these systems process information remains challenging due to difficulties in defining appropriate multivariate metrics and ensuring their scalability to large systems. To address these challenges, we introduce a novel framework based on what we call "Shannon invariants" -- quantities that capture essential properties of high-order information processing in a way that depends only on the definition of entropy and can be efficiently calculated for large systems. Our theoretical results demonstrate how Shannon invariants can be used to resolve long-standing ambiguities regarding the interpretation of widely used multivariate information-theoretic measures. Moreover, our practical results reveal distinctive information-processing signatures of various deep learning architectures across layers, which lead to new insights into how these systems process information and how this evolves during training. Overall, our framework resolves fundamental limitations in analyzing high-order phenomena and offers broad opportunities for theoretical developments and empirical analyses.

Bits and Pieces: Understanding Information Decomposition from Part-whole Relationships and Formal Logic

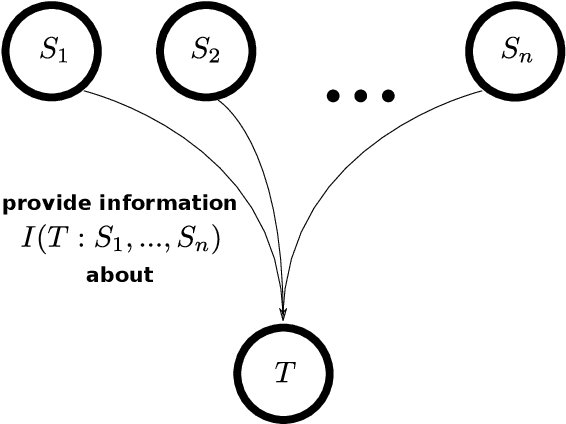
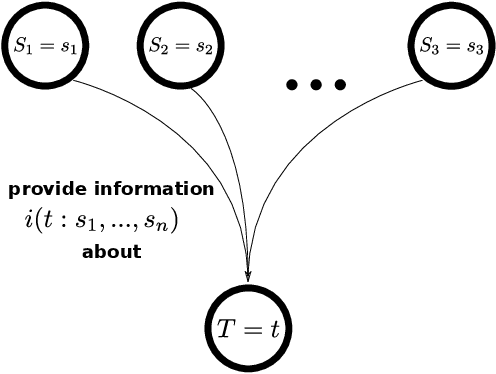
Partial information decomposition (PID) seeks to decompose the multivariate mutual information that a set of source variables contains about a target variable into basic pieces, the so called "atoms of information". Each atom describes a distinct way in which the sources may contain information about the target. In this paper we show, first, that the entire theory of partial information decomposition can be derived from considerations of elementary parthood relationships between information contributions. This way of approaching the problem has the advantage of directly characterizing the atoms of information, instead of taking an indirect approach via the concept of redundancy. Secondly, we describe several intriguing links between PID and formal logic. In particular, we show how to define a measure of PID based on the information provided by certain statements about source realizations. Furthermore, we show how the mathematical lattice structure underlying PID theory can be translated into an isomorphic structure of logical statements with a particularly simple ordering relation: logical implication. The conclusion to be drawn from these considerations is that there are three isomorphic "worlds" of partial information decomposition, i.e. three equivalent ways to mathematically describe the decomposition of the information carried by a set of sources about a target: the world of parthood relationships, the world of logical statements, and the world of antichains that was utilized by Williams and Beer in their original exposition of PID theory. We additionally show how the parthood perspective provides a systematic way to answer a type of question that has been much discussed in the PID field: whether a partial information decomposition can be uniquely determined based on concepts other than redundant information.